(1)問題
なめらかに動くピストンがついたシリンダー内に理想気体を入れたところ、圧力P0、体積V0、温度T0になった。この状態から、図に示す三つの過程により、気体の体積をV1に減少させる。過程(a)は断熱変化、過程(b)は等温変化、過程(c)は定圧変化である。
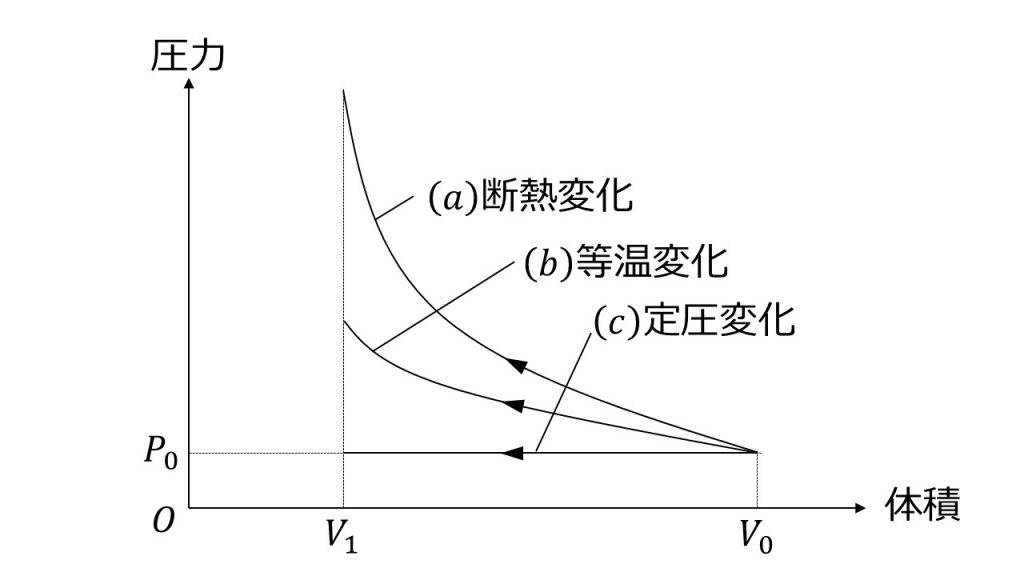
①過程(a)~(c)のうち熱の出入りがない過程と、内部エネルギーが変化しない過程を答えよ。
②過程(a)~(c)において、気体が外部からされる仕事をそれぞれWa, Wb, Wcとする。これらの大小関係を答えよ。
③過程(a)~(c)を、縦軸を体積、横軸を温度としたグラフで表せ。ただし、縦軸にV0とV1を、横軸にT0を記すこと。
(2015年センター試験本試物理第5問改)
(2)答案
①熱の出入りがない過程:過程(a)、内部エネルギーが変化しない過程:過程(b)
②圧力を縦軸に、体積を横軸にとったグラフにおいて、気体が外部からされる仕事は、グラフと横軸で囲まれた面積で表される。ただし、体積が減少するときは気体は外部から仕事をされ、体積が増加するときは気体は外部へ仕事をする。
よって
Wc<Wb<Wa
③過程(a):断熱変化では、体積が減少したとき、温度は上昇する(断熱圧縮)。ただし、直線にはならない。
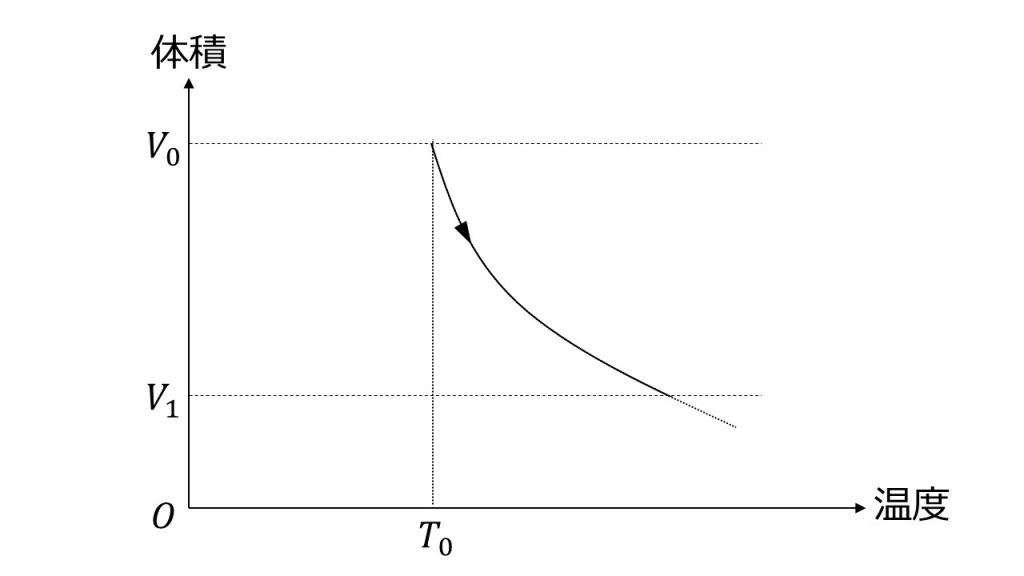
過程(b):等温変化では、体積が減少しても、温度は変化せずに一定に保たれる。
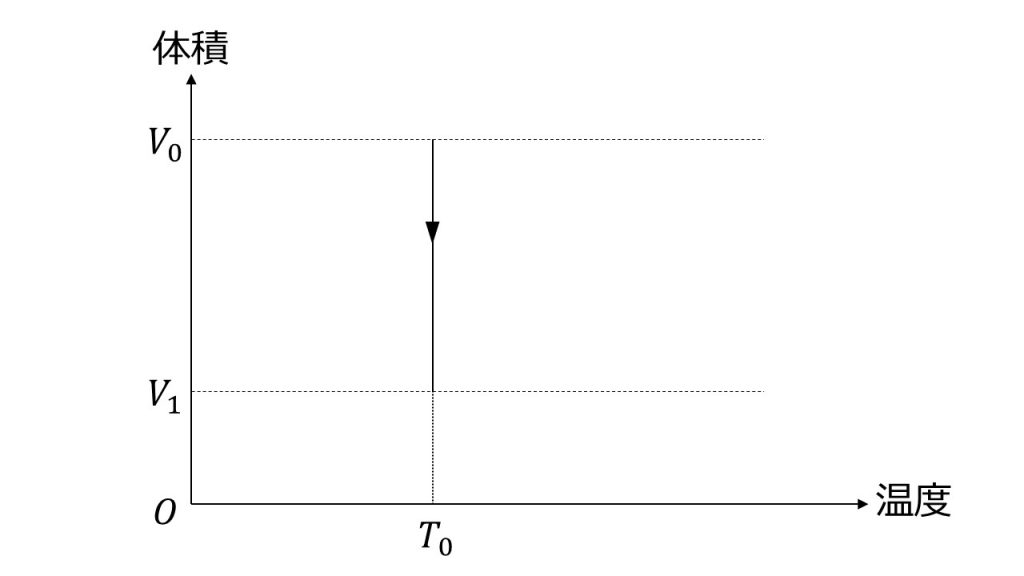
過程(c):理想気体の状態方程式pV=nRTより
V=nRT/p
定圧変化では、pは一定なので、VはTに比例する。
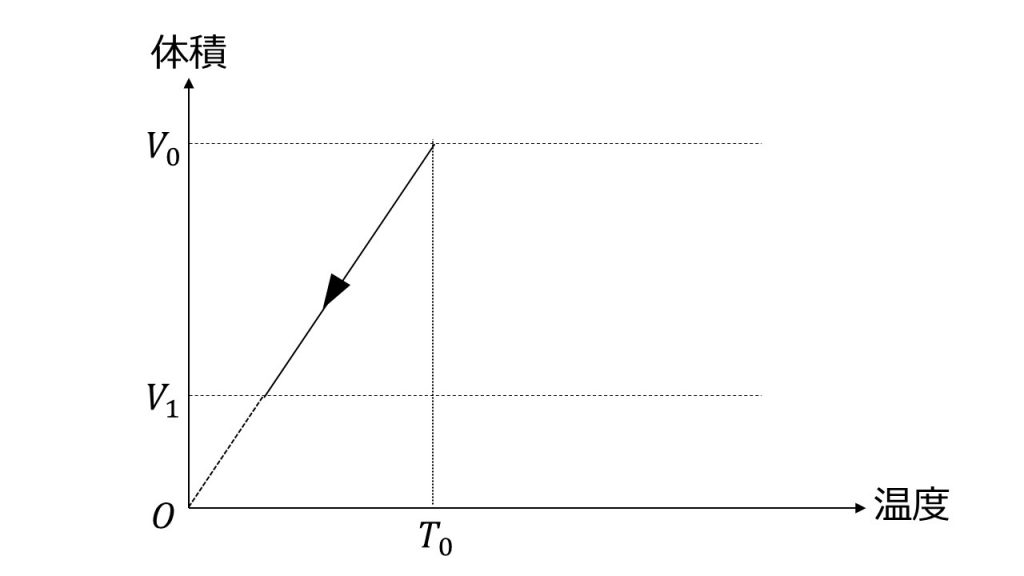
(3)解法のポイント
P-Vグラフにおいて、仕事は、グラフと横軸で囲まれた面積で表されるということは重要です。ただし、体積が減少するときは気体は外部から仕事をされ、体積が増加するときは気体は外部へ仕事をすることになります。
また、グラフをかく問題の基本は
(縦軸の文字)=(横軸の文字を使った式)
の形にすることです。
ちなみに断熱変化は、
pVγ=一定
という式が成り立っています(ポアソンの法則)
γは比熱比と呼ばれ、その値は気体分子の種類によって変わります(単原子分子や二原子分子など)
そのため、P-VグラフやV-Tグラフが直線となることはありません。
さらに断熱変化においては、Q=0となるため、熱力学第一法則より
ΔU=Win
となります。
したがって、仕事をされる(体積が減少する)と内部エネルギーは増加し、温度は上昇します。また、仕事をする(体積が増加する)と内部エネルギーは減少し、温度は低下します。
(4)必要な知識
①定圧変化

②等温変化

③断熱変化
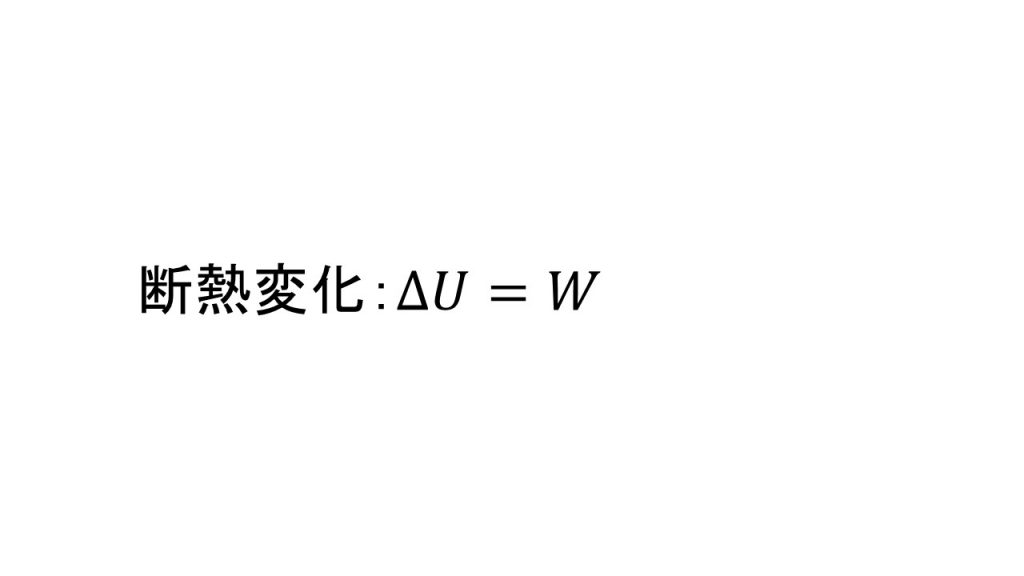
④理想気体の状態方程式

⑤熱力学第1法則


(5)理解すべきこと
①定積変化・定圧変化・等温変化・断熱変化におけるp-VグラフとV-Tグラフ(ポアソンの法則についても解説しています)
②理想気体の状態方程式の使い方と計算の工夫の仕方を確認しましょう→理想気体の状態方程式の使い方解説動画(理想気体とは何か、混合気体の考え方、計算の工夫の仕方についても解説しています)
③気体の内部エネルギーの表し方解説動画(内部エネルギーの増加量の3つの表し方、熱力学の第1法則、定積変化、定圧変化、等温変化、断熱変化、マイヤーの関係についても解説しています)
④気体が吸収した熱量の求め方解説動画(定積モル比熱、定圧モル比熱、熱力学の第1法則、定積変化、定圧変化、等温変化、断熱変化、熱効率)
⑤気体が外部にする仕事(pΔVになるわけ、p-Vグラフ、熱機関のサイクル、定積変化、定圧変化、等温変化、断熱変化、断熱自由膨張)
