(1)例題

(2011年センター試験本試数学ⅡB第1問改)
(2)例題の答案


(3)解法のポイント
sinθとcosθの和と積を両方含んでいる場合は、
t=sinθ+cosθとおいて考えます。
ポイントとしては、以下のことに注意しましょう。
①sin2θ=2sinθcosθ とする。
②t²=(sinθ+cosθ)²=1+2sinθcosθとなるので、
sinθcosθ=(t²-1)/2
③t=sinθ+cosθと置き換えてtの関数とするのだが、tの範囲を求めないといけない(文字を導入したら、範囲を求める)
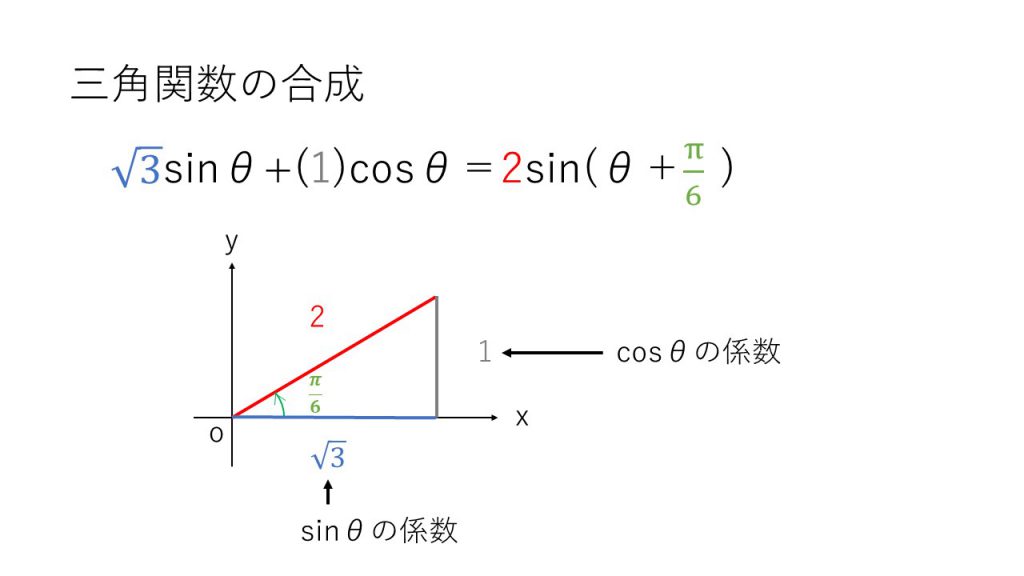
→t=sinθ+cosθ=√2sin(θ+π/4)と合成して、tの範囲を求める
④tの二次関数になることが多いので、二次関数の最大・最小を求めるときに縦に引くべき3つの線を引く。
①範囲
②範囲の真ん中
③軸
(4)必要な知識
①2倍角の公式
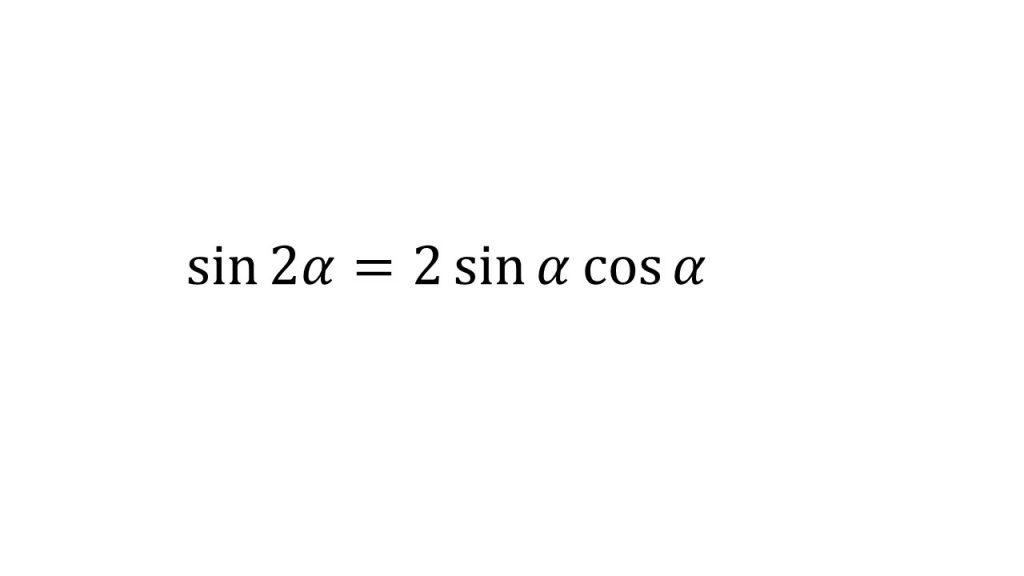
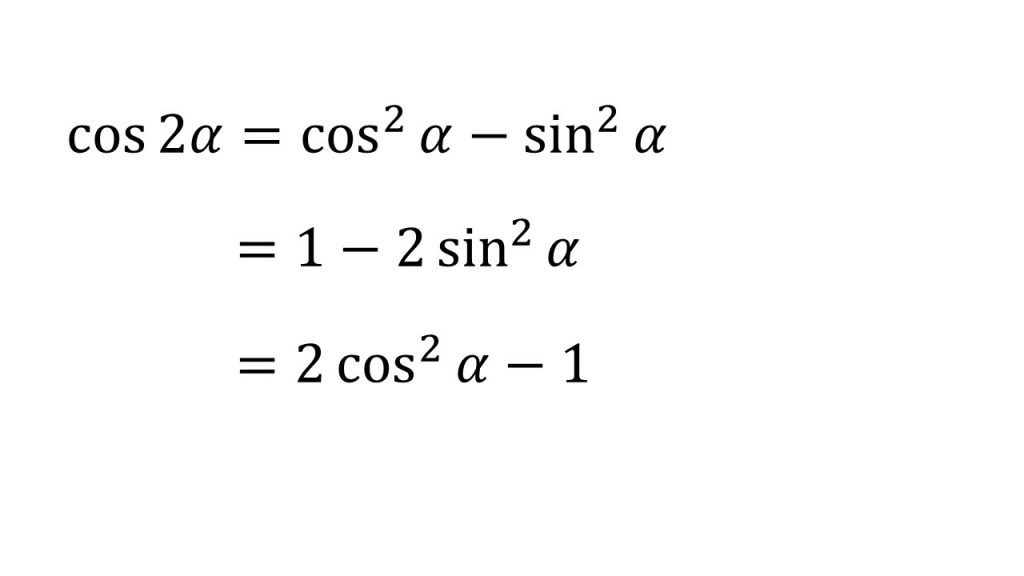
②三角関数の合成
(5)解説授業動画
