(1)ポイント
f(n)-g(n)の極限を考えるとき
- f(n)の次数≠g(n)の次数→+∞または-∞に発散
- f(n)の次数=g(n)の次数→極限値が存在するかもしれない(発散する可能性もある)→分母または分子の有理化をする。
※f(n)の次数=g(n)の次数のときは、∞-∞の不定形となるので、そのまま極限を求めることができない。
(2)演習問題
☆問題のみはこちら→根号(ルート)を含む式の極限(数学Ⅲ)をマスターしよう!(問題)
①
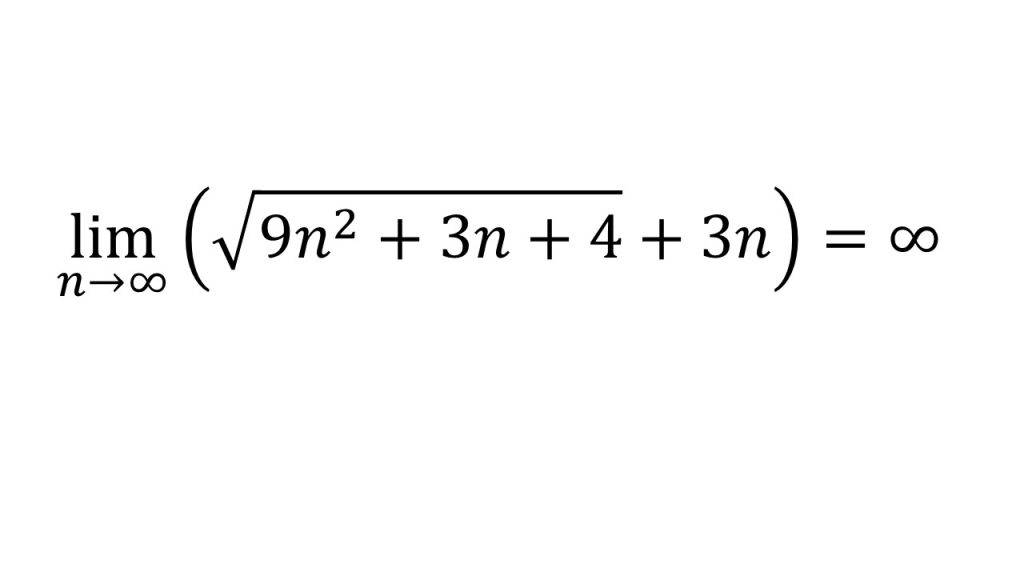
- √9n2+3n+4と3nはともに∞に発散するので、∞+∞=∞となる。
②
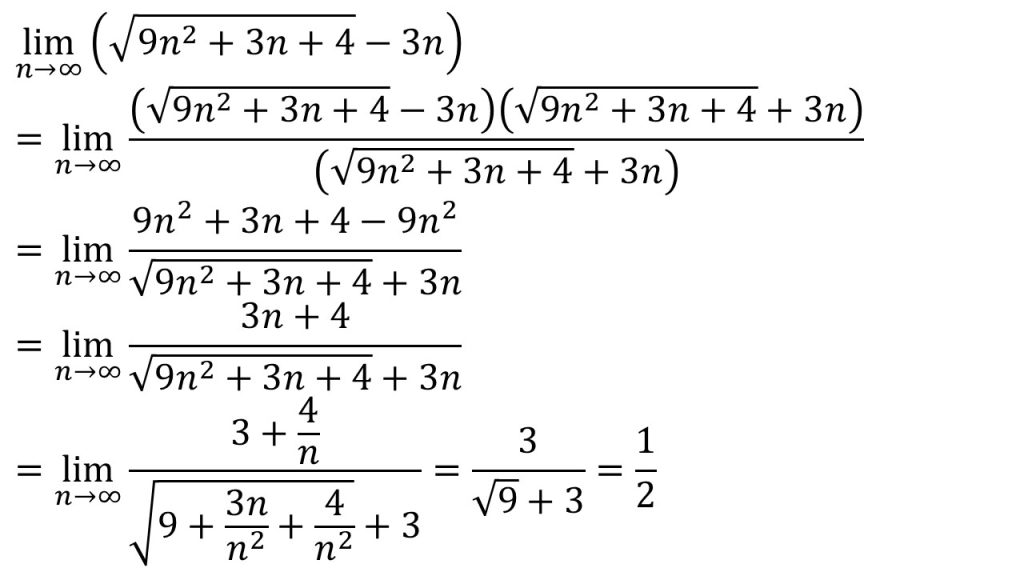
- f(n)の次数=g(n)の次数なので、極限値が存在する可能性がある→分子の有理化をする。
- 分数式の極限値を求めるときは、最も次数の大きい項で分母と分子を割る。今回はn2で割る。
③
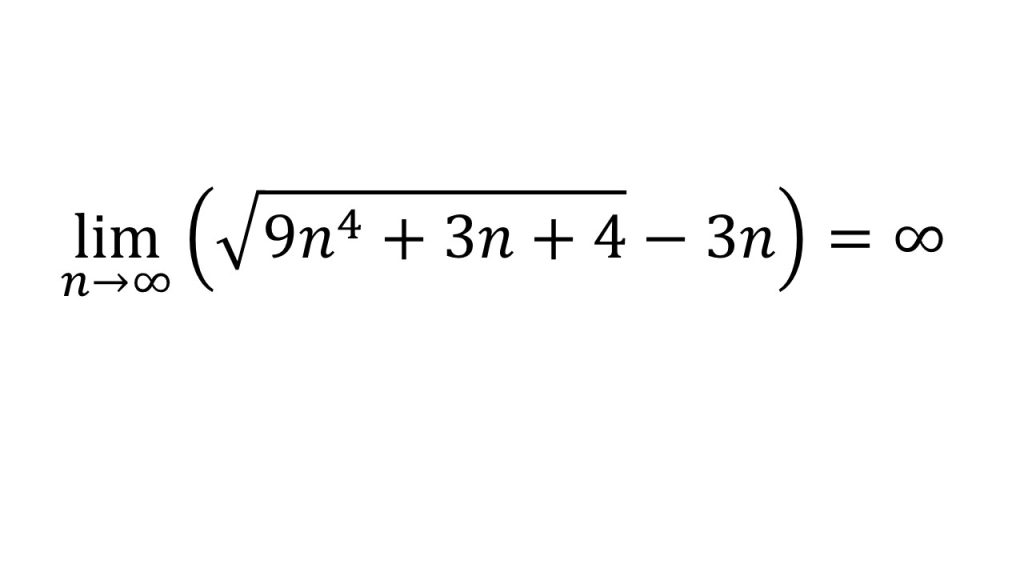
- √9n4+3n+4の次数は2で、3nの次数は1なので∞に発散する。イメージとしては、(変化の大きいもの)-(変化の小さいもの)となるので、結局+∞になってしまう。
④
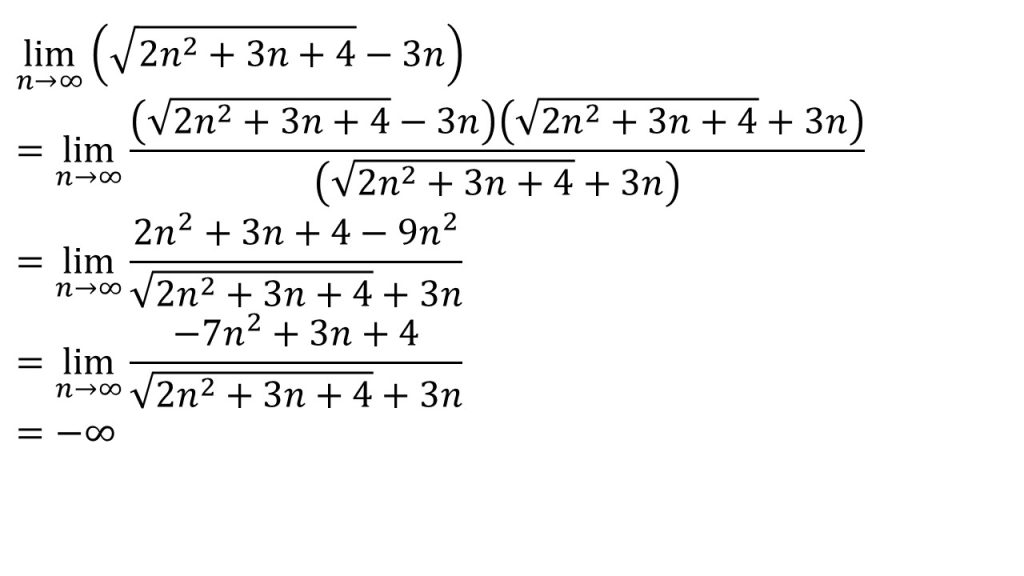
- f(n)の次数=g(n)の次数なので、極限値が存在する可能性がある→分子の有理化をする。
⑤
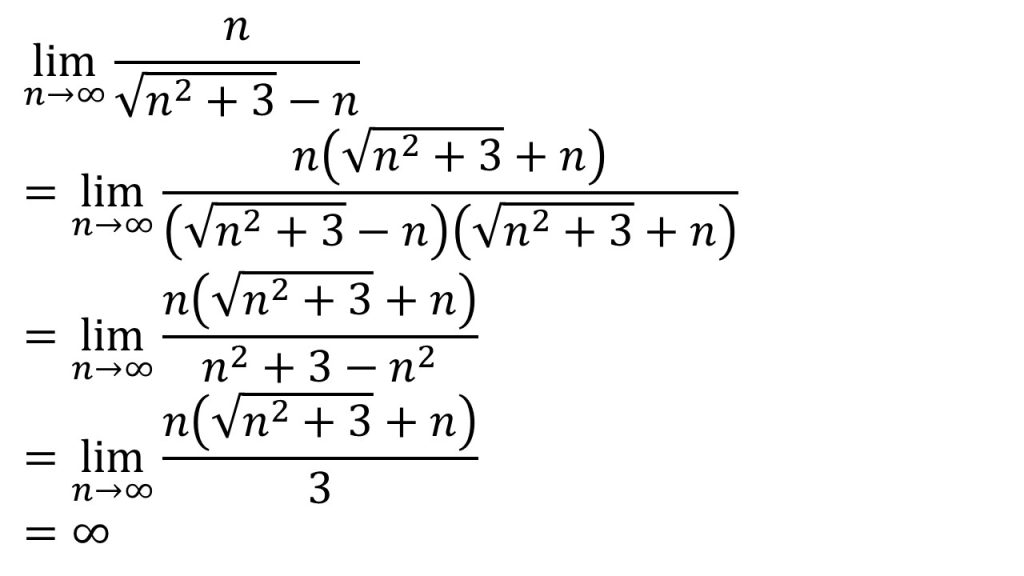
- 分子の次数=分母の次数なので、極限値が存在する可能性がある→分母の有理化をする。
⑥

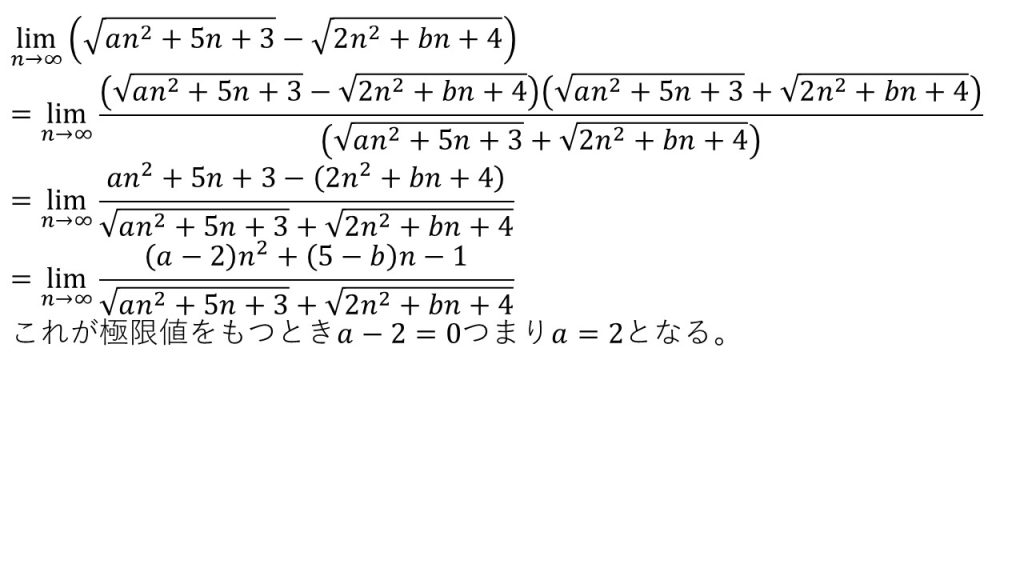
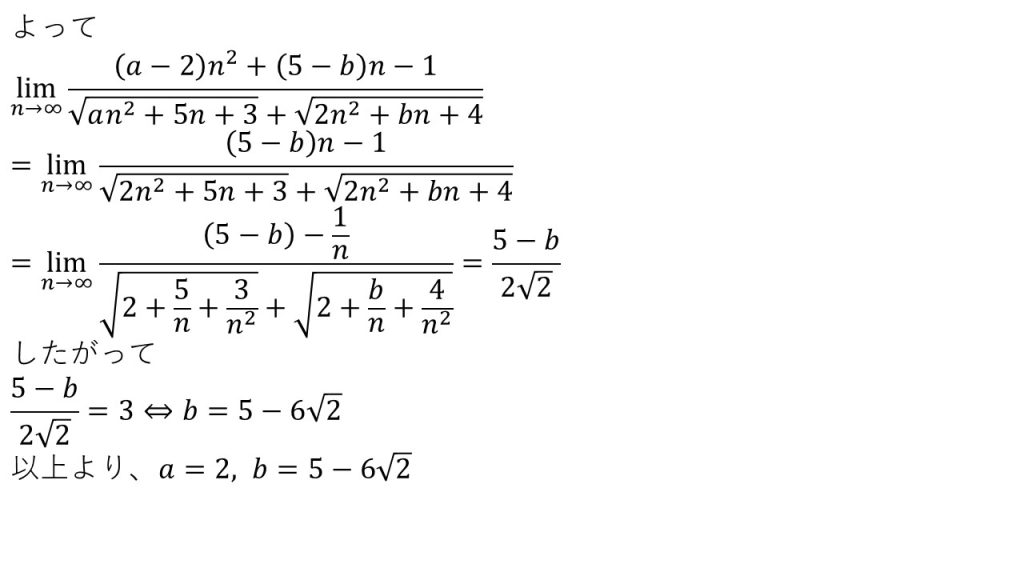
- f(n)の次数=g(n)の次数なので、とりあえず分子の有理化をする。
- 分数式は、分子の次数≦分母の次数とならなけば発散してしまうので、分母の次数を下げるためにn2の係数を0にする。
☆問題のみはこちら→根号(ルート)を含む式の極限(数学Ⅲ)をマスターしよう!(問題)
