(1)例題
aを正の定数とする。3次関数f(x)=x3-2ax2+a2xの0≦x≦1における最大値を求めよ。
(2)例題の答案
f'(x)=3x2-4ax+a2=(3x-a)(x-a)
f'(x)=0とすると、x=a/3, a
a>0より、f(x)の増減表は以下のようになる。
| x | … | a/3 | … | a | … |
| f'(x) | + | 0 | - | 0 | + |
| f(x) | ↗ | 極大 4a3/27 | ↘ | 極小 0 | ↗ |
ここでx=a/3以外にf(x)=4a3/27を満たすxの値を求める。
x3-2ax2+a2x=4a3/27
⇔ (x-a/3)2(x-4a/3)=0
x≠a/3のときx=4a/3
つまり、f(x)はx=4a/3のとき4a3/27となる(極大値と同じ高さになる)
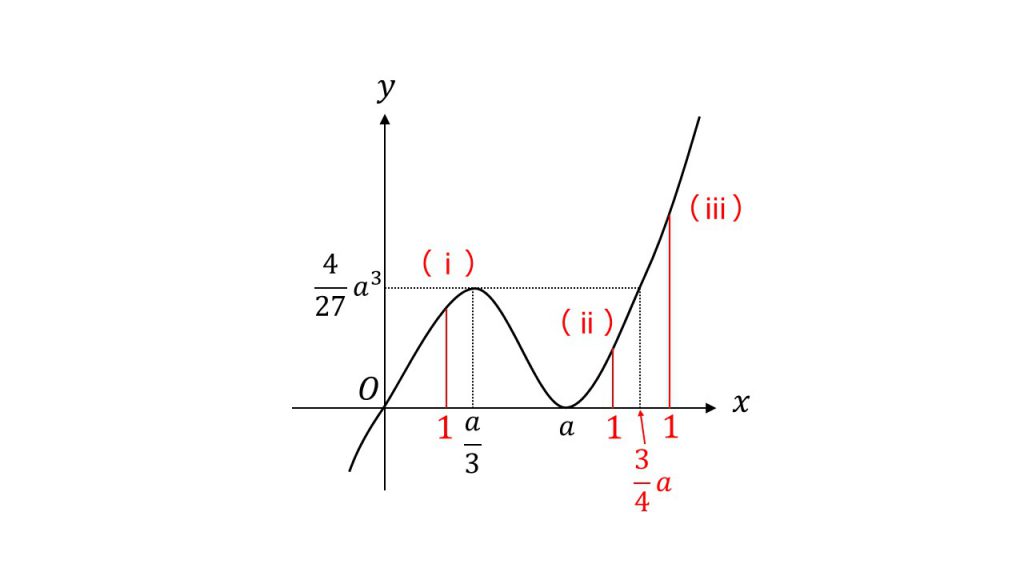
したがって、
(ⅰ)1<a/3 つまり a>3のとき
x=1のとき、最大値a2-2a+1
(ⅱ)a/3≦1≦4a/3 つまり 3/4≦a≦3のとき
x=a/3のとき、最大値4a3/27
(ⅲ)0<4/3a<1 つまり 0<a<3/4のとき
x=1のとき、最大値a2-2a+1
(ⅰ)~(ⅲ)をまとめると
0<a<3/4, 3<aのとき、x=1で最大値a2-2a+1
3/4≦a≦3のとき、x=a/3で最大値4a3/27
(3)解法のポイント
3次関数の最大・最小の問題の答えの候補となる場所は、
①極値(極大値または極小値)
②範囲の左端
③範囲の右端
この3つです。
基本の流れとしては、
グラフをかいて→範囲の線を動かしていき、①~③の場所を確認しながら場合分けを考える
となります。
しかし、このとき注意すべき場所が2カ所あります。
①極大値または極小値と同じ高さの場所
②区間の両端が同じ高さになる場所
この2つに注意しましょう。
今回の問題で言えば、
極大値4a3/27と同じ高さになる場所が、x=4a/3となり、
この場所が場合分けの境目となっています。
※区間の両端が同じ高さになる場所を求めるパターンの問題はこちら→区間に文字を含む3次関数の最大・最小(区間の端が同じ高さになる場所も確認する)
