(1)例題
図aのように、極板間の距離が3dの平行板コンデンサーに電圧V0を加えた。次に、帯電していない厚さdの金属板を、図bのように極板間の中央に、極板と平行となるように挿入した。極板と金属板の面は同じ大きさ同じ形である。また、図aおよび図bのように、左の極板からの距離をxとする。図中には、両極板の中心を結ぶ線分を破線で、x=dおよびx=2dの位置を点線で示した。
図a
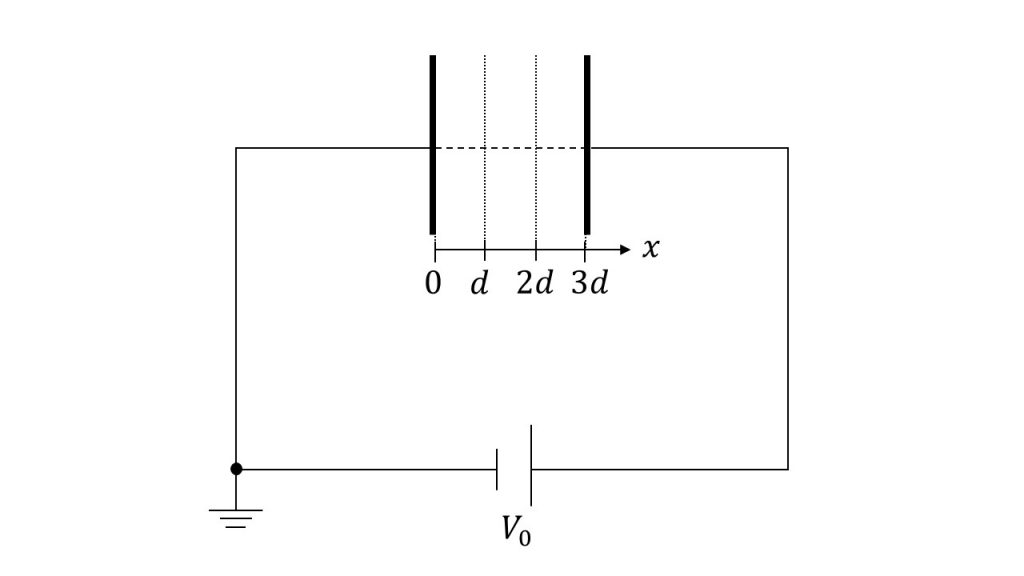
図b

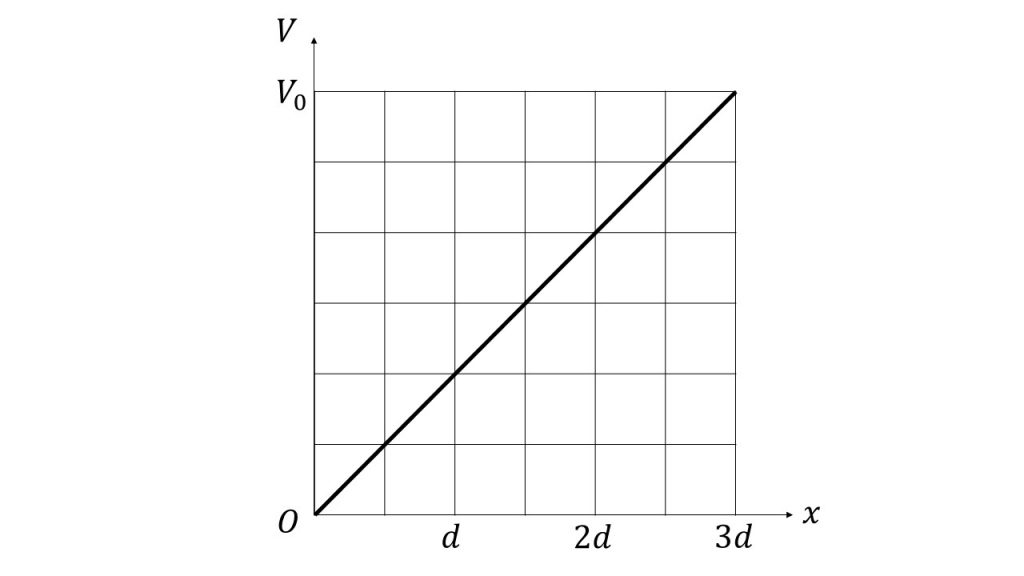
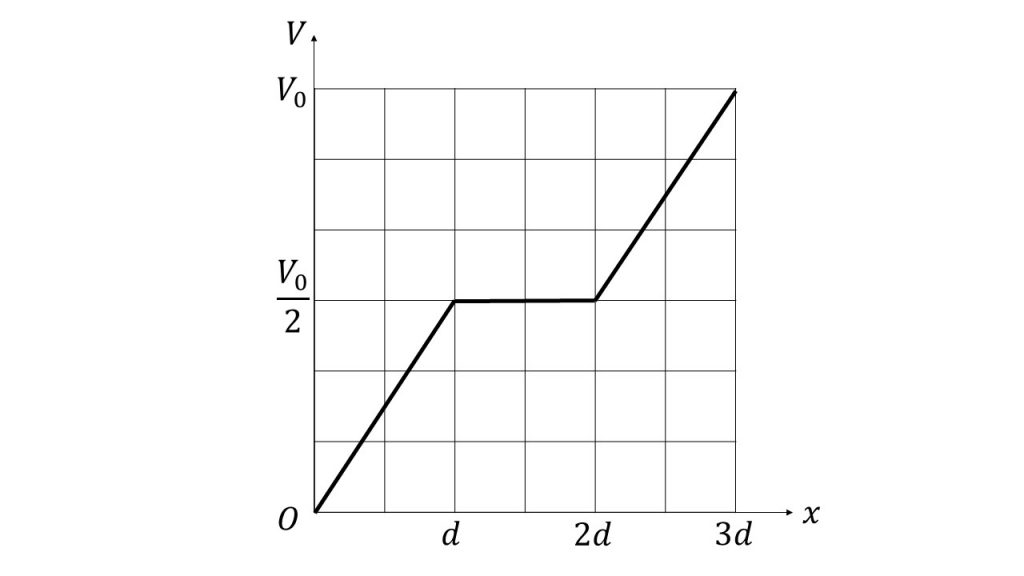
①図aおよび図bにおいて、十分長い時間が経過した後の、両極板の中心を結ぶ線分上の電位Vとxの関係を表すグラフをそれぞれかけ。
②十分長い時間が経過したあとの、図aのコンデンサーに蓄えられたエネルギーをUa、図bの金属板が挿入sレ田コンデンサーに蓄えられたエネルギーをUbとする。Ua:Ubを求めよ。
(2017年センター試験本試物理第2問A)
(2)例題の答案
①



②

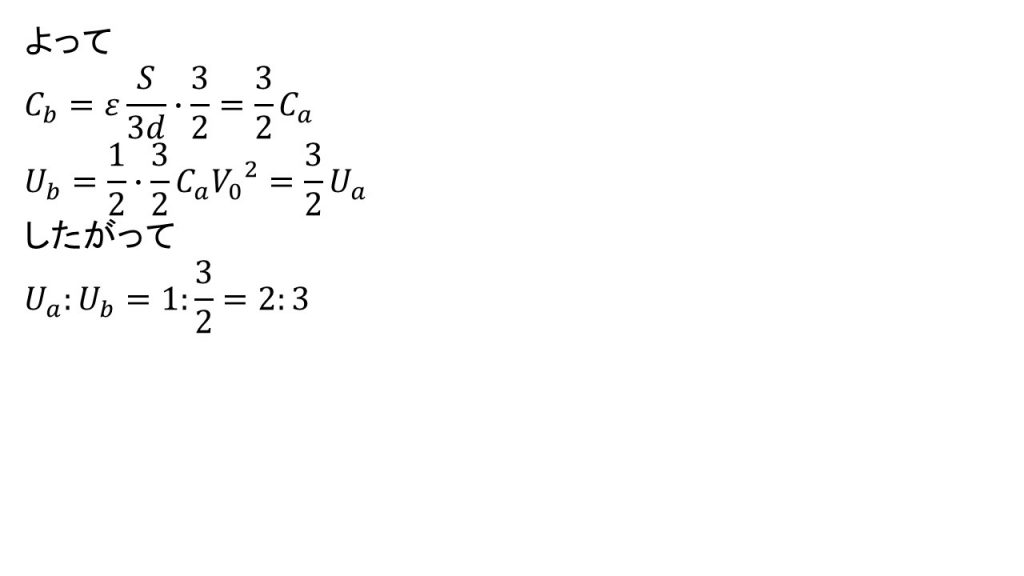
(3)解法のポイント
しっかりと電場と電位を区別しましょう。電場は電位の傾きを表します。イメージとして、電位は山や谷の高さを表し、電場はその坂の傾きを表していると考えましょう。
そうすれば、電場が0のときは傾きが0なのであって、高さ(電位)は0ではないということが理解できると思います。
まず、平行版板コンデンサーの極板間の電場は一様であるということは知っておきましょう。
また、コンデンサーに金属板を金属板を挿入した場合、金属板内の電場は0となり、2つのコンデンサーが導線で直列につながれているとみなすことができます。
あるいは、極板間の距離が金属板の厚さ分小さくなったと考えることもできます。今回で言えば、金属板を挿入したことによって、極板間の距離が3dから2dに変化したと考えます。
(4)必要な知識
①電位の式

②電気容量

③静電エネルギー

(5)理解すべきこと
①コンデンサーに導体板(金属板)と誘電体を挿入したときの考え方(隙間がないときと隙間があるときの両方解説しています)
②電場と電位とは何かを理解しましょう(「場」とは何か、力学(重力)と電気を対応させて理解する、静電気力、クーロンの法則、静電気力による位置エネルギー(静電エネルギー)、電場と電位をイメージで理解する)
