(1)解説授業動画
☆YouTubeチャンネルの登録をよろしくお願いします→大学受験の王道チャンネル
(2)解説授業の原稿
二重根号の外し方
√(ルート)の中に√があるものを二重根号と呼びます。
二重根号となっているものは、√を1つにすることができます。
そのやり方は2つあり、中の√の前が+のときと、-のときの2つの外し方があります。
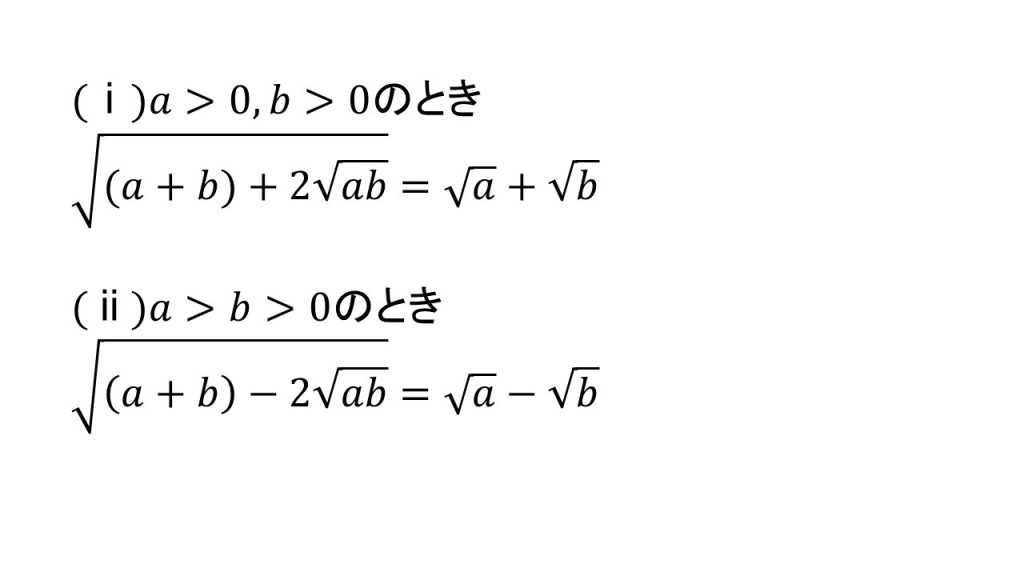
a, bがともに正のとき、√の中が
和+2√積
の形にできれば、二重根号を外すことができ、a, bがともに正で、bよりもaが大きいとき、√の中が
和-2√積
の形にできれば、二重根号を外すことができます。
ポイントは、中の√の前を2にしておくということです。このような形を作ることができれば、二重根号を外して√が1つの形にすることができます。
なぜ二重根号が外れるのか
ちなみに、なぜこのような形にできれば、二重根号を外すことができるかというと、√a+√bを2乗してみるとa+b+2√abとなり、この等式の両辺に√をつけてみると、(ⅰ)の式となり、同様に、√a-√bを2乗したらa+b-2√abとなり、この等式の両辺に√をつけてみると、(ⅱ)の式となるからです。
例題(1)
それでは具体的に例題で確認してみます。

このような問題があったとき、これら二重根号を外してみます。
まずは、√の中の√の前の数字が2になっていることを確認します。(1)は元々、2になっているので、もうこのまま外すことができます。
足して9、かけて14となる2つの整数を考えると、7+2が9で、7×2が14なので、
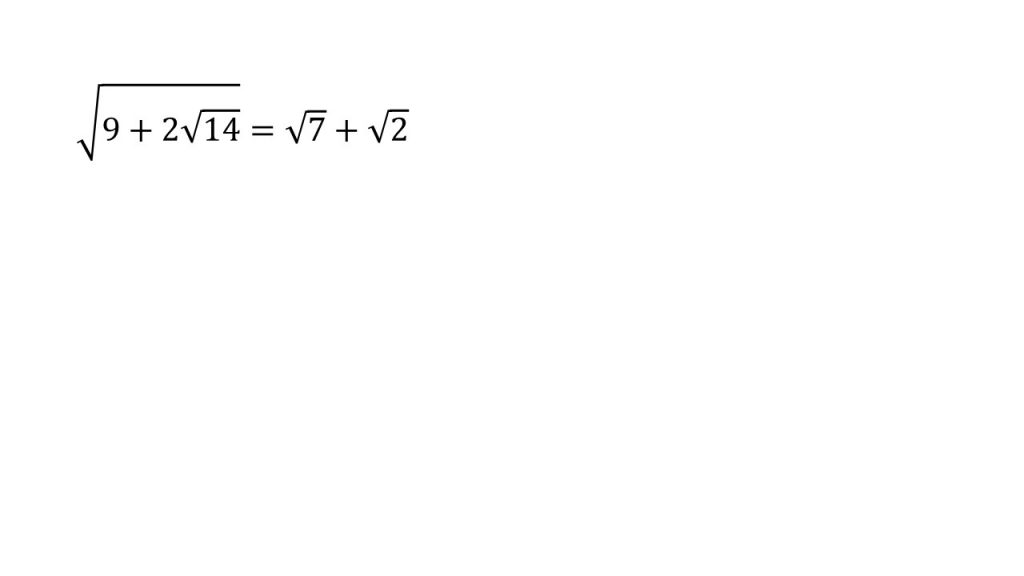
となります。
例題(2)
次に(2)ですが、こちらは中の√の前の数字が2になっていません。そういった場合は、中の√の前の数字を2として、√の中を2×4つまり8とします。
こうすることで、中の√の前が2になったので、この二重根号を外すことができ、足して6、かけて8となる数字を考えて、4+2が6で、4×2が8なので、

となります。符号がマイナスのときは、
(大きいもの)-(小さいもの)
になるように注意しましょう。
例題(3)
次に(3)でも二重根号を外してみます。
今回も中の√の前が2となっていません。こういった場合は、中の√の前が2となるように式変形します。
このように、√84を2√21とすることで中の√の前を2とします。そして、中の√の前が2となったので、足して10、かけて21となる数字を考えて、7+3が10で、7×3が21なので、
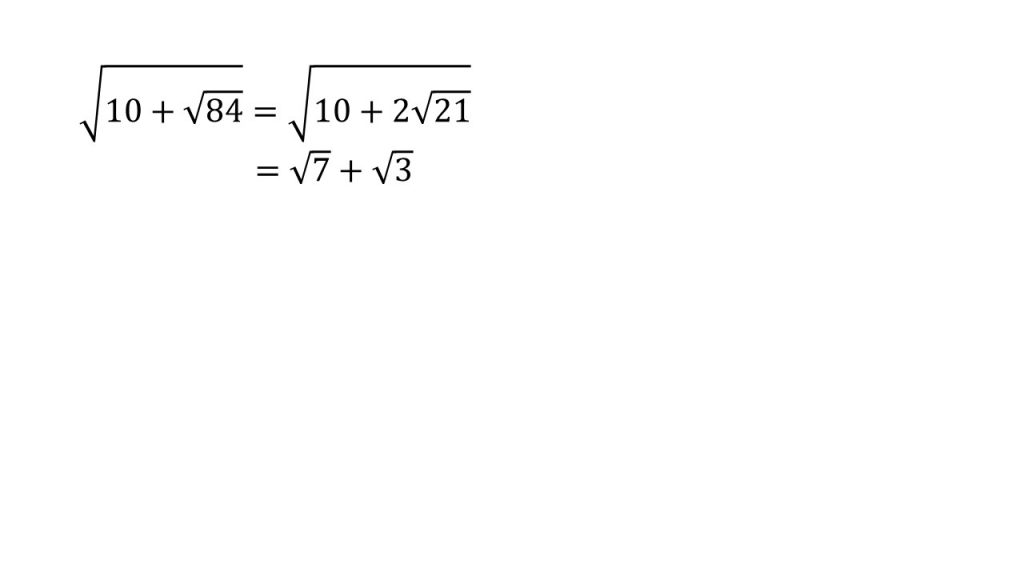
となります。
例題(4)
最後に(4)でも、二重根号を外してみます。
今回も中の√の前の数字が2となっていません。更に√15は先ほどのように2を外に出すこともできません。
こういった場合はどうしたらよいかというと、√2を分母とした分数にします。√2を分母 とした場合、分子にも√2を掛けないといけません。つまり分子は、

となります。ここで√30としないように注意してください。
そして、中の√の前の数字が2となったので、足して8、かけて15となる数字を考えて、5+3が8、5×3が15なので、分子は√5+√3となります。
分母が無理数なので、分母と分子に√2をかけて有理化します。すると、答えが
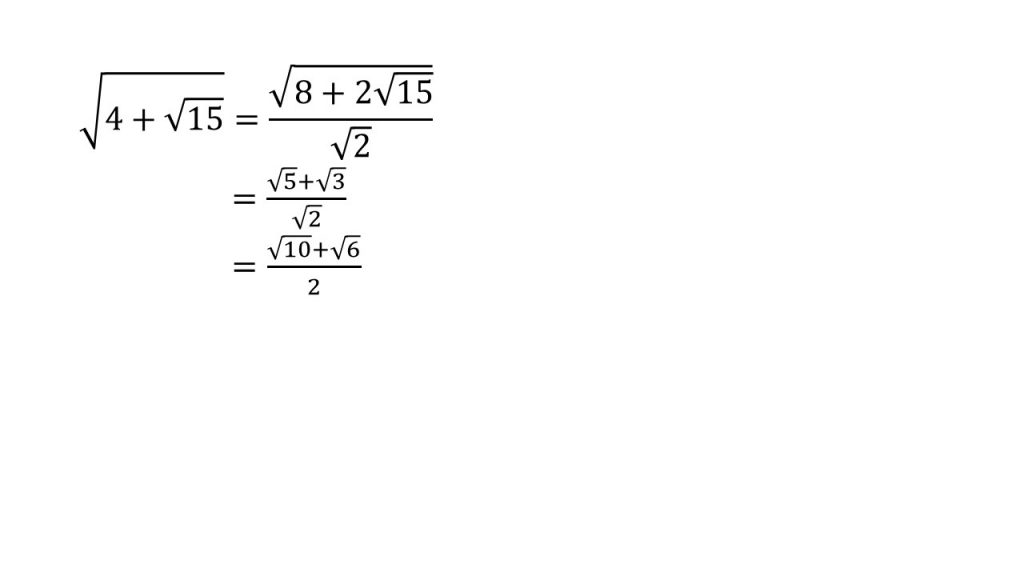
となります。
(3)解説授業の内容を復習しよう
①二重根号
(4)実数(数学Ⅰ)の解説一覧
①数の分類一覧(複素数、実数、有理数、無理数、整数、自然数、素数)
②根号(ルート)の中に2乗があるときの対処法(根号(ルート)は「正の平方根」という意味です)
④根号や虚数単位iを含む式を代入して式の値を求める問題の解法(次数下げ)
※虚数を習っていない場合は、後半を飛ばしてください。
⑤数学で守らないといけないルール(文字で割るときの注意点、係数に文字を含む方程式の解法、係数に文字を含む不等式の解法)
