(1)例題

(2)例題の答案

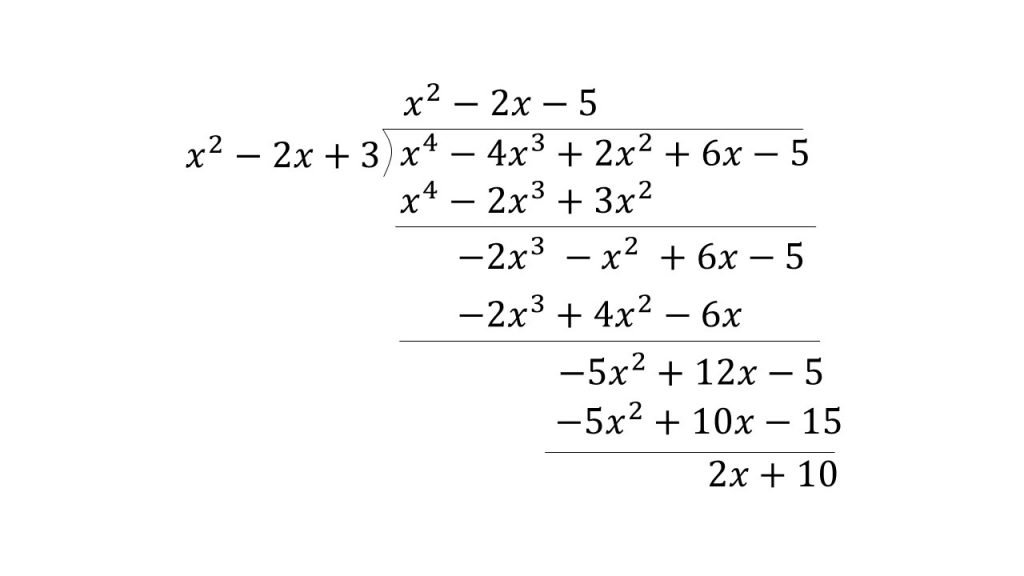
(3)解法のポイント
x=〇のときの高次式(次数が3以上の整式)の値を求める問題で、〇には、根号や虚数が含まれる場合の解法です。
式の値を求めるときは、まずは代入を考えると思いますが、今回はそのまま代入すると計算が大変です(もちろんそのまま代入して計算しても間違いではないので求めることはできますが)
そこで、次数下げを考えます。
①まずは、x=〇を式変形して、
(根号の項)=~~、または、(虚数の項)=~~
の形にします。
②そして、①で変形した式の両辺を2乗します。すると、根号やiがなくなります。
③つぎに、②で2乗した後の式を、xの降べきの順(ax²+bx+c=0の順番)に並べ替えます。
④そして、元の整式P(x)を③で並べ替えた式の左辺の2次式ax²+bx+cで割ります。
⑤商をQ(x)、余りをdx+eとすると、
P(x)=(ax²+bx+c)Q(x)+dx+e
となるわけですが、x=〇のときax²+bx+c=0なので、求める式の値は、
P(〇)=d〇+e
となります。
このような手順で解けば、⑤の段階で計算する式の次数が下がり、ラクに正確に計算できるようになります。
(4)理解すべきこと
次数下げのやり方を理解しましょう→根号や虚数単位iを含む式を代入して式の値を求める問題の解法(次数下げ)
☆動画はこちら↓
