(1)解説授業動画
☆YouTubeチャンネルの登録をよろしくお願いします→大学受験の王道チャンネル
(2)解説授業の原稿
電場と電位について解説します。
電場や電位の理解が曖昧な方や電場と電位の区別がついていない方も多いと思います。今回の解説で、電場と電位をしっかり区別して正確に理解するようにしましょう。
「場」とは何か
まずは電場について解説します。
電場を理解するためには、まず場とは何かについて理解しましょう。場とは、そこにいるだけで力がはたらく空間のことです。
重力場
例えば地球上にいる我々は、重力場の中にいます。重力場にいれば、何もしていなくても重力という力を受けます。このように、そこにいるだけで重力がはたらく空間を重力場といいます。
重力場の中であれば、地球から離れている物体でも重力を受けます。場の力というものは、その場を生み出しているものと接触していなくてもはたらくのです。
電場
電場もこの重力場と同じように考えることができます。
例えば下図のように、+Qの電荷を固定したとします。
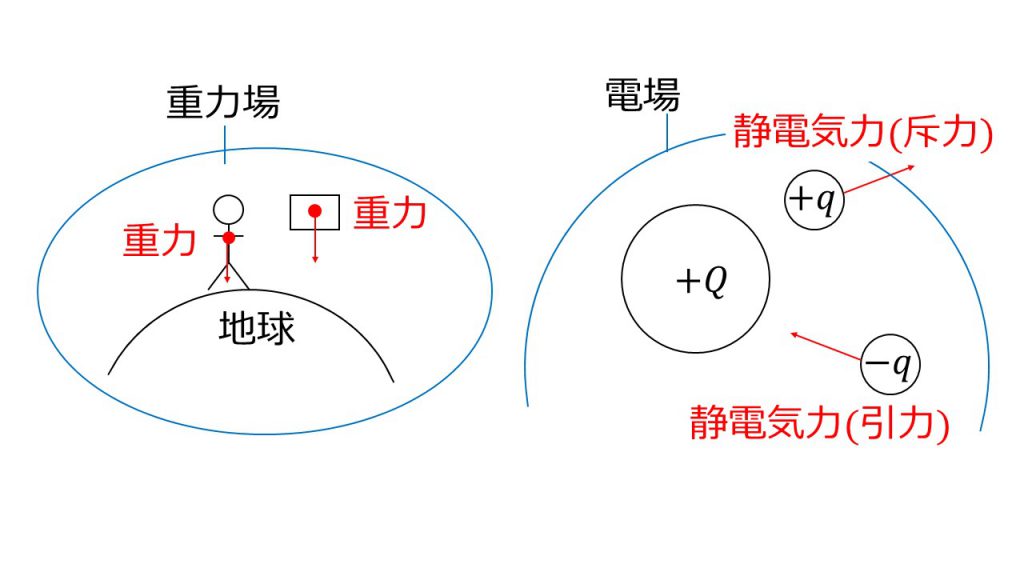
このとき、+qの別の電荷をおいてみたら、電荷同士は接触していないのに、+qの電荷は静電気力を受けます。ともに正の電荷なので、反発する力つまり斥力を受けます。
また、-qの別の電荷をおいてみたら、お互いに接触しているわけではないのにこの電荷は静電気力を受けます。こちらは正の電荷と負の電荷なので引っ張られる力つまり引力を受けます。
このように電荷をおくと、何もしていないのに斥力を受けたり引力を受ける場がつくられます。この電荷が作る場のことを電場というのです。
静電気力(電場から受ける力)
それでは、電場が何か理解できたところで、次は電荷から受ける力の大きさを確認します。
電場から受ける力のことを静電気力というのですが、その表し方は2通りあります。
F=qE
F=k0×Qq/r2
この2通りの表し方があるのですが、これらも重力と対応させると理解しやすくなります。
F=qEを重力と対応させて理解する
まずはF=qEから考えてみます。
例えば、重力加速度gがはたらく重力場の中に、質量mの物体をおいてみると、mgの重力がはたらきます。同様に、大きさがEの電場がはたらく空間に+qの電荷をおいてみると、qEの静電気力を電場の向きと同じ向きに受けます。
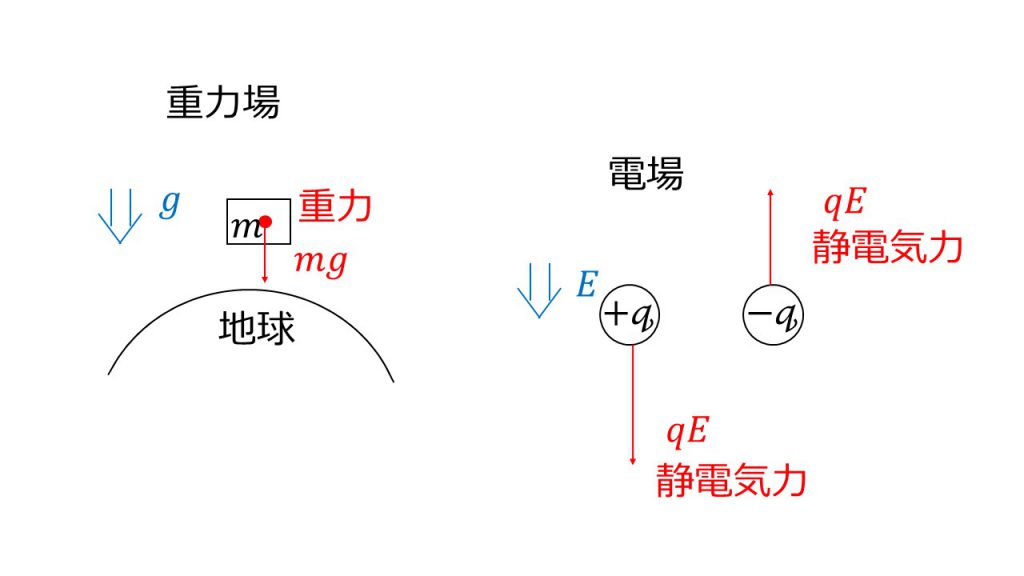
このように重力加速度と電場、質量と電荷を対応させると理解しやすくなります。
ちなみに、-qの電荷をおくと、電場の向きとは逆向きにqEの大きさの力を受けることになります。このように、重力は重力加速度と同じ向きにしかはたらきませんが、電場から受ける力は電荷の正負によってその向きが変わるので注意してください。
F= k0×Qq/r2を万有引力と対応させて理解する
それでは次に、F= k0×Qq/r2について確認します。こちらの式は、力学の万有引力の考え方と対応させると理解しやすくなります。
下図のように質量Mの地球の中心からr[m]離れた位置にある質量mの物体は、地球と接触していなくても、F=G×Mm/r2の万有引力を受けます。これと同様に、+Qの電荷からr[m]離れた位置に-qの電荷をおいたとき、この-qの電荷は何もしなくてもF= k0×Qq/r2の静電気力を受けます。

どちらもr2が分母にあるので、rつまり距離が小さくなればなるほど、大きな力を受け、rが大きくなればなるほど小さな力となります。また、このGとk0はともに比例定数であり、それぞれ決まった値となっています。
そして、F= k0×Qq/r2の式のことをクーロンの法則と呼んでいます。
ちなみに、r[m]離れた位置に+qの電荷をおくと、大きさがk0×Qq/r2となる逆向きの力を受けることになります。このように静電気力は電荷の符号によって受ける力の向きが変わるので注意してください。
電場の大きさを求める
また、地球の半径をRとして、遠心力を無視すると、重力=万有引力とすることができ、この等式から重力加速度の大きさを求めることができます。
mg= G×Mm/R2
∴ g=GM/R2
同様に、電場から受ける力=クーロンの法則による静電気力とすることで、電場の大きさを求めることができるということも知っておきましょう。
qE= k0×Qq/r2
∴ E= k0×Q/r2
静電エネルギーを重力による位置エネルギーと対応させて理解する
それでは次に、電位について解説します。
電位とは何かについて理解するために、まず静電気力による位置エネルギーを重力による位置エネルギーと対応させながら理解しましょう。ちなみに静電気力による位置エネルギーのことを、静電エネルギーともいいます。
例えば、重力加速度gがはたらく重力場の中に質量mの物体があったとします。その物体にはmgの重力がかかりますが、その物体をhの高さまで持ち上げたとします。すると、この物体はmghの重力による位置エネルギーを得ることになります。

この物体を持ち上げた後、手を離すと、この物体は落下します。それはつまり、重力によって仕事をされているということなので、重力により位置エネルギーを得るということは、重力によって仕事をされる可能性を得るということにもなります。
同様に、大きさEの一様な電場の中で+qの電荷をおくと、先ほども確認した通り電場の向きと同じ向きにqEの静電気力をこの電荷は受けることになります。その状態で電荷をd[m]だけ移動させるとqEdの静電気力による位置エネルギーを得ることになります。

この電荷も移動させた後に離すと、重力場で物体が落下するように、電荷もひとりでに電場の向きに移動します。これはつまり、静電気力により位置エネルギーを得るということは、静電気力によって仕事をされる可能性を得るということになります。
このように、静電気力による位置エネルギーは重力による位置エネルギーと対応させることで理解しやすくなります。
ただし注意点があり、今回は「電場は一様である」としています。「一様である」とは、「電荷がどの位置にあっても電場の大きさと向きは変わらない」という意味です。
電位の定義
静電気力による位置エネルギーが理解できたところで、電位の定義を確認してみます。
電位の定義は
V=Ed
となります。
つまり、電位とは単位電荷あたりの静電気力による位置エネルギーといえます。もう少し簡単にいうと、大きさが1クーロンの電荷が得ることのできる位置エネルギーであるということになります。
先ほど確認した通り、静電気力による位置エネルギーは、qEdで表されます。ここでV=Edとすれば、静電気力による位置エネルギーは、qVとなります。このように、電位に電荷の大きさをかけることで、静電気力による位置エネルギーを求めることができます。
電位を重力で対応させて理解する
電位は重力場におけるghに相当すると考えると理解しやすくなります。
例えば、重力場において基準からhの高さの位置に質量mの物体をおくと、その物体はmghの位置エネルギーを得ます。また、質量2mの物体をその位置におくと、2mghの位置エネルギーを得ます。
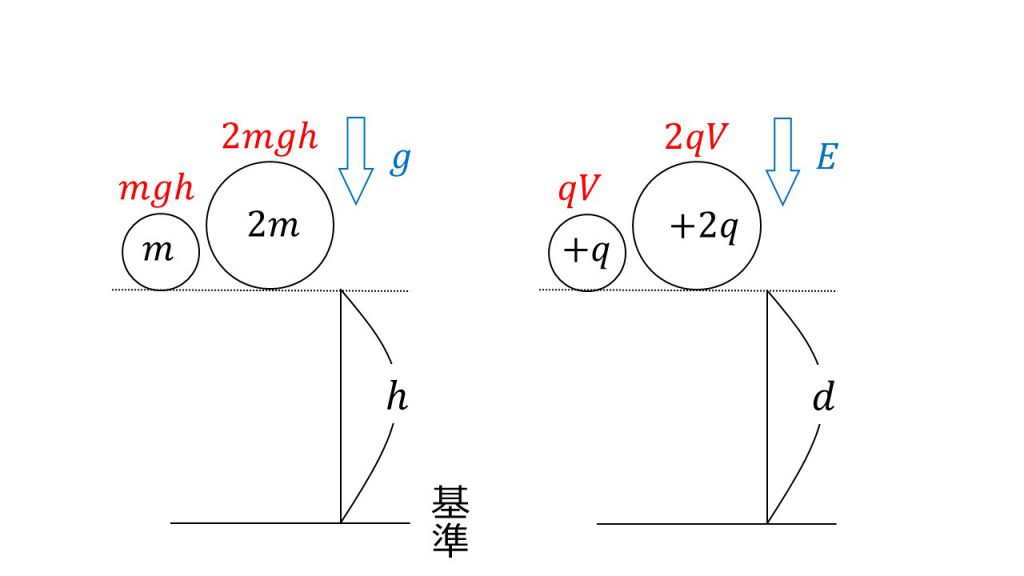
これと同様に、一様な電場がはたらいている中で基準からd離れた位置に+qクーロンの電荷をおくと、qVの位置エネルギーを得ます。また、+2qクーロンの電荷をおくと2qVの位置エネルギーを得ます。
このように、電位とは、その位置に電荷をおいたときにどれだけの静電気力による位置エネルギーを得ることができるかを表しています。
力学と電気の対応関係
それではこれまでに出てきた力学と電気の対応関係をまとめます。
力学における質量(m)は、電気の世界では電荷あるいは電気量(q)に対応します。電気量とは、電荷の量のことです。
そして、力学における重力加速度(g)は電気の世界では電場(E)で、力学における高さ(h)は電気の世界では基準からの距離(d)で、力学における重力(mg)は電気の世界では静電気力(gE)に対応します。
また、力学の世界ではghに名前はついていませんが、電気の世界でghに対応するのはEdあるいはVの電位です。
そして、力学における重力による位置エネルギー(mgh)は電気の世界では静電エネルギーつまり静電気力による位置エネルギー(qEd)と対応します。
このように、電気の単元を学習するときは力学と対応させると理解しやすくなります。
電場と電位のイメージ
電場と電位が何か確認できたところで、より実践的に使えるようになるために電場と電位のイメージによるとらえ方を解説します。電場は傾き、電位は高さとイメージすると理解しやすくなります。
電位は高さで、電場は傾き
例えば、下図のように正電荷をおくと山ができ、負電荷をおくとこのように谷ができるとイメージします。
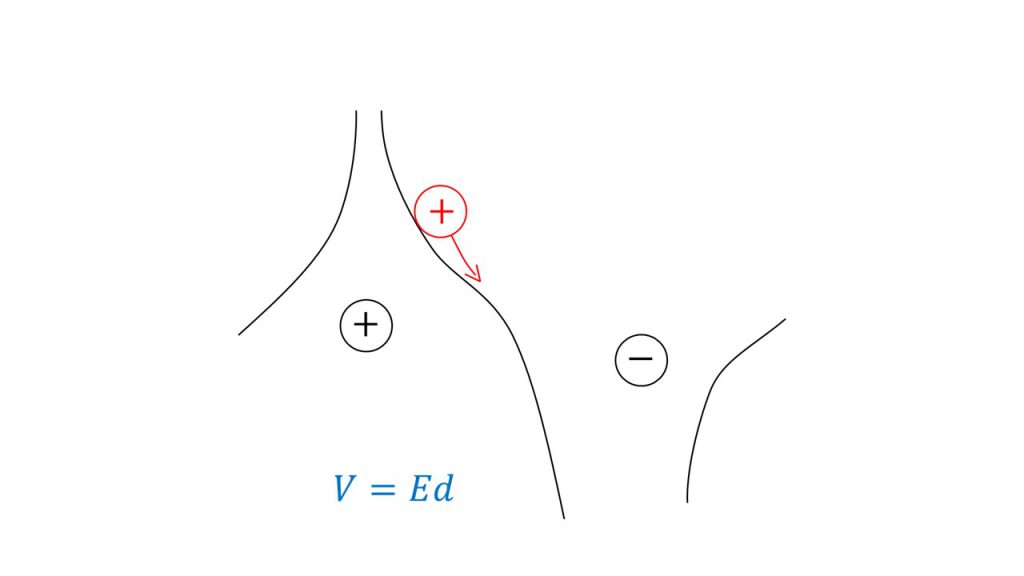
すると、この山や谷の高さが電位となり、その傾きが電場となります。
そして、斜面に玉をおいたとき、玉はひとりでに低い方に転がっていくのと同様に、下図のような電位の状態で正電荷をおくとこの電荷は電位が高い方から低い方へひとりでに移動します。これは電場によって電荷が力を受けるのを、斜面によって転がっているとイメージしているのです。
「電位が高いけど電場は0」ということもある
このように電場がイメージできれば、電位の傾きが急であるところは電場が大きいということになり、電位の傾きが緩やかなところは電場が小さいということであり、電位の傾きが0であるということは電場も0であるということが理解できます。
特に注意したいのが、下図のように電位は高いけれどその傾きがない場所つまり電位差がない場所に電荷をおいても、その電荷には力がはたらかず、動くことはないということもあります。
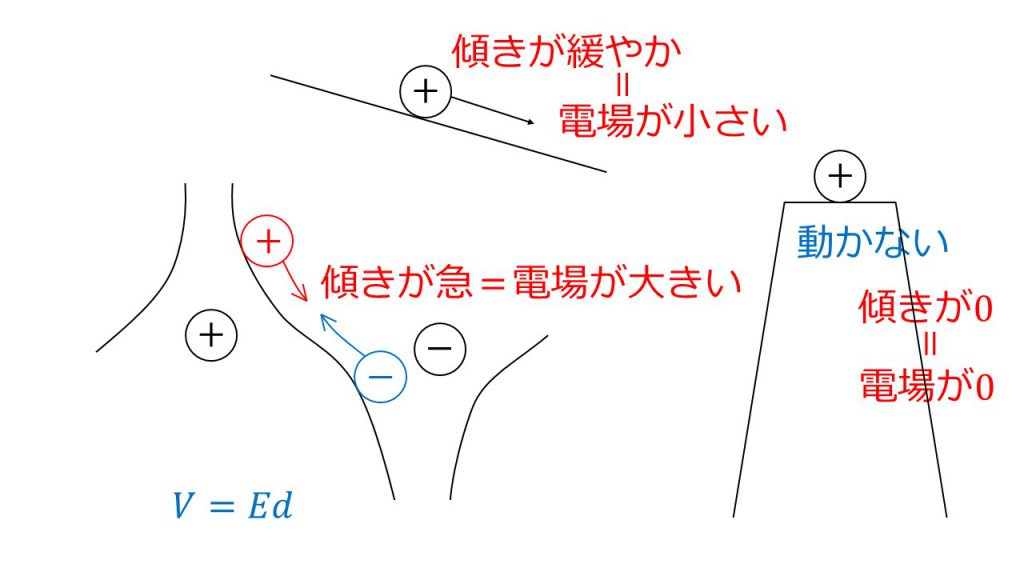
電場はあくまで傾きなので、高電位だけど電場が0ということもあり得るので注意してください。
ちなみに、V=Edという電位の定義の式を見ても、電場が電位の傾きであるということが分かります。例えばy=axであれば、aが傾きとなるように、V=Edであれば、EはVの傾きであるという意味の式になっています。
また、もう一点注意したいことは、負電荷をおいた場合は高い方から低い方へ転がるのではなく、低い方から高い方へ登って行くということが力学の世界とは違う点なので注意してください。
(3)解説授業の内容を復習しよう
(4)電場と電位(電磁気)の解説一覧
②電場と電位とは何かを理解しましょう(「場」とは何か、力学(重力)と電気を対応させて理解する、静電気力、クーロンの法則、静電気力による位置エネルギー(静電エネルギー)、電場と電位をイメージで理解する)
③ガウスの法則はいつどのように使うべきか(電気力線とは何か、電気力線と電場の関係、ガウスの法則の使い方、金属球・金属板・導体棒が作る電場)
④静電誘導と誘電分極(静電遮蔽、雷が発生したとき車の中が安全な理由についても解説しています)
(5)参考
☆物理の解説動画・授業動画一覧(力学・熱力学・波動・電磁気・原子)
☆物理に関する現象や技術(力学、熱力学、波動、電磁気、原子)
