☆問題のみはこちら→積分(数学Ⅱ)の解法パターン(問題)
①不定積分をした後の検算方法は?
→微分をして元に戻るか試してみる。
②積分変数がtのとき(dtとなっているとき)は、xはどう扱う?
→tとは無関係であれば、定数として扱う。
③不定積分の答えを書くときに忘れてはいけないものは?
→積分定数のCを書くこと
④定積分で計算ミスをしないためにすること3つ
→ⅰ)積分をした後は、微分をして元に戻るか確認すること
ⅱ)F(b)-F(a)の段階で、-の後ろに( )をつけること
ⅲ)分母が同じ分数を先に計算する(通分は最後)
⑤xの関数の中にtの定積分が含まれていたらどうする?
→=aとおく(定数として扱う)
⑥インテグラルを含む関数はどうする?
→両辺を微分する。
⑦積分で面積を求めるときの式
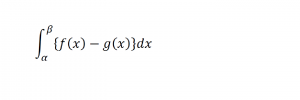
において、α, β, f(x), g(x)はそれぞれ何を表すか。
→αは左端、βは右端、f(x)は上にくるグラフ、g(x)は下にくるグラフ
⑧グラフの上下関係(どちらが上でどちらが下か)が判断できないときは、どうするか。
→引き算をする(数学において大小関係を調べるときは引き算をする)
⑨⅙公式はどのようなときに使うか、2つ答えよ。
→放物線と直線で囲まれた面積を求めるとき、2つの放物線で囲まれた面積を求めるとき
⑩面積を求めるとき、どのような図形を探してみるか。
→三角形や台形(これらの面積を求めるときは積分をする必要はない)
⑪絶対値を含む関数の定積分のやり方は?
→ⅰ)積分をする関数(絶対値を含む関数)のグラフをかく。
ⅱ)積分区間がα≦x≦βなら、x=α、x=βの縦線を引く。
ⅲ)ⅰのグラフとx軸とx=α、x=βで囲まれた面積を求める
⑫絶対値を含む関数のグラフのかき方を2通り説明せよ。
→ⅰ)全体が絶対値に含まれている→絶対値の中のグラフをかいてx軸で折り返す
ⅱ)絶対値を含む→絶対値の中が0以上か0より小さいかで場合分け
