(1)解説授業動画
☆YouTubeチャンネルの登録をよろしくお願いします→大学受験の王道チャンネル
(2)解説授業の原稿
今回は溶解度の計算の解説をします。
溶解度とは何か
まずそもそも溶解度とは何かを確認します。
溶解度とは溶媒100gに溶けうる溶質の最大質量のことです。
注意したいのは溶媒100gであるということです。溶液ではなく溶媒であることに注意してください。大抵の場合、溶媒は水なので「水100gに最大でどれぐらい溶けるのか」を表していると考えると良いでしょう。
溶解度の計算のポイント
続いて計算をするときのポイントを3つ確認します。
ポイント①
まず溶解度の計算の基本は、「飽和溶液であれば溶質、溶媒、溶液の比は、温度を変えない限り一定である」ということです。
「この比が一定であるということを使って方程式を立てて解く」というのが溶解度の計算の基本方針となります。
ただし注意したいのは、溶質と溶媒と溶液の比が一定になるのは飽和溶液のときだけであり、飽和溶液でない溶液の場合は、比を使って方程式を立てることができないので注意してください。
ポイント②
そのため次のポイントは、「飽和溶液であるかの確認が必要である」ということです。
溶質が溶解度まで溶けている溶液のことを飽和溶液というので、問題文をよく読み、その溶液が飽和溶液であるかどうかを確認しましょう。
問題文に直接「飽和溶液である」と書いてあればもちろんその溶液は、飽和溶液なのですが、「溶質が溶けきれずに析出した」と書いてある場合もその溶液は飽和溶液である、と判断することができます。
なぜなら溶解度とは溶けうる溶質量の最大質量、つまり限界を表しており、溶解度を超えた量の溶質は析出するので、溶質が溶けきれずに残っている場合は、その溶液の溶質は溶解度まで達していると考えられるからです。
ポイント③
そして最後のポイントは、飽和溶液の溶質と溶媒と溶液の比が必要になるので、溶質と溶媒と溶液の質量をまとめた表を作っておくと計算がしやすくなるということです。実際にどのような表をつくればよいかは、この後問題を解きながら解説します。
なお毎回溶質、溶媒、溶液と書くのは面倒なので、今後は溶質のことは「し」、溶媒のことは「ば」、溶液のことは「え」と書くようにします。
それではこのポイントに注意しながら実際に問題を解いてみます。
問題①:飽和溶液を冷却する
まずは以下のような問題を解いてみます。なお今回扱う問題は、すべて有効数字は3桁で答えます。
塩化カリウムの水に対する溶解度は、20℃で34.2、80℃で51.3である。80℃における飽和溶液50gを20℃に冷却すると、何gの塩化カリウムが析出するか求めてみましょう。
最初の状態の溶質・溶媒・溶液の表を作る
まずは「80℃における飽和溶液」と書いてあるので、80℃における溶質、溶媒、溶液の表をつくります。

「ケース」というのは今回の問題の場合における溶質と溶媒と溶液の質量のことで、「モデル」というのは溶解度の値をつかった溶質、溶媒、溶液の質量のことです。
今回は80℃なのでモデルの溶質は溶解度の51.3gとなります。そして溶解度というのは溶媒100gに対して解ける溶質の量なので、モデルの溶媒は100となります。よってモデルの溶液の質量は51.3+100=151.3となります。
このように、まずはモデルの行を埋めます。
そして次に、ケースの行を埋めていきます。
問題文には飽和溶液50gとかいてあるので、ケースの溶液が50gということになります。
そして、ケースのうち1つが埋まると、残りは自動的に決まっていきます。なぜなら飽和溶液であれば溶質、溶媒、溶液の比は一定となるので、溶液が50gになったとしても、溶質と溶媒と溶液の比は51.3:100:151.3となります。
モデルを50/151.3倍したらケースとなるので、ケースの溶質の質量は51.3×50/151.3となり、ケースの溶媒の質量は100×50/151.3gとなります。
これでこの問題の80℃における飽和溶液の溶質、溶媒、溶液の質量の質量がわかりました。なお、これらは問題の答えではないので計算はせずにとっておくようにしましょう。
後の状態の溶質・溶媒・溶液の表を作る
そして、この飽和溶液を「20℃に冷却すると塩化カリウムが析出した」とあるので、20℃においても飽和溶液であると判断することができます。
したがって20℃の場合の表も作っていきます。
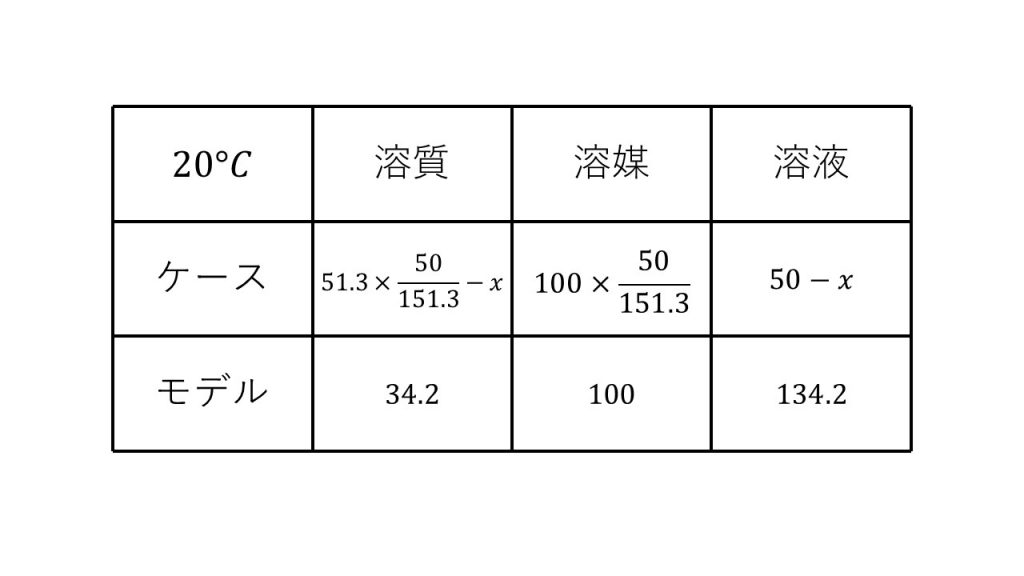
20℃における溶解度は34.2なので、モデルの溶質は34.2となり、モデルの溶媒は100であり、モデルの溶液は134.2となります。
そして次に今回のケースの溶質と溶媒と溶液を書いていきます。ただし、今回は析出した塩化カリウムの質量を求める問題なので、求めるものをx[g]とおき、xを含めてこの3つを埋めていきます。
まずは溶質です。今回析出した塩化カリウムは溶けきれなかった溶質なので、20℃における今回の溶質の質量は、51.3×(50/151.3)-xとなります。つまり80℃の溶質から析出したxグラムをひいたものになります。
そして次に溶媒ですが、これは80℃のときと変わりません。なぜなら析出したのは溶質であり溶媒に変化はないからです。
そして最後に溶液ですが、溶質がxグラム減り、溶媒が変化していないので溶液は50-xとなります。これで20℃における溶質と溶媒と溶液の質量を、xをつかって表すことができました。
方程式を立てる
ここまでできればあとは方程式を立てるだけです。どのようにして方程式を立てるのかというと、「表のケースとモデルの間の線を分数の線だと考えて、各列を=で繋ぐという」イメージで方程式をつくります。
つまり、
51.3×(50/151.3)-x/34.2=100×50/151.3/100=50-x/134.2
という関係が成り立つのです。
なぜこうなるかというと飽和溶液であれば、溶質と溶媒と溶液の比が変わらないからです。つまり
ケースの溶質:ケースの溶媒:ケースの溶液=モデルの溶質:モデルの溶媒:モデルの溶液
という比例式が成り立つので、
ケースの溶質/モデルの溶質=ケースの溶媒/モデルの溶媒/=ケースの溶液/モデルの溶液
という方程式を立てることができます。
今回、文字はxの1つなので、この3つのうちから計算しやすい2つを選んで解くようにしましょう。今回は溶媒と溶液の式を使うと計算しやすくなります。
工夫しながら方程式を解く
それではあとは方程式を解いていきましょう。なるべく工夫をしながら正確にかつ速く解くようにしましょう。
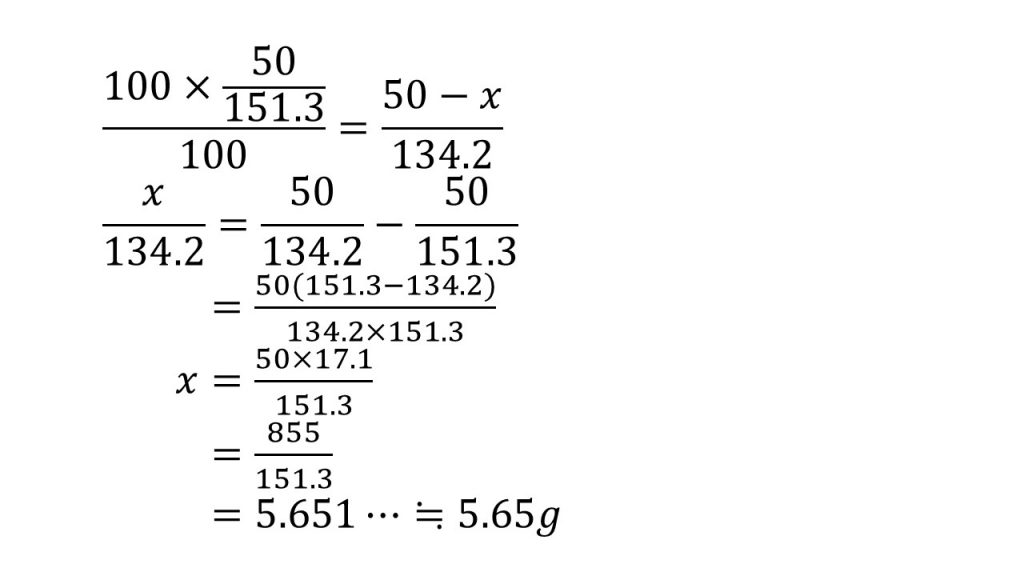
まず、簡単に約分にできるところは約分しておきます。次に、求めたい文字を含む項は左辺に、それ以外の項は右辺にもっていきます。そして、分数の足し算や引き算になっているときはまず通分をします。
そして、両辺を134.2倍することで左辺の分母をはらい、右辺の分子が因数分解できたので因数分解しておきます。すると、もう約分はできそうにないので分子を計算します。そして最後に割り算をして、有効数字が3桁になるように四捨五入して、答えは5.65gとなります。
いかがでしょうか。溶解度の計算は飽和溶液の表を作って方程式を立てるということ、そして、方程式を解くときは工夫をすることで、楽に速く解けるようになるということ、この2点が重要です。
問題②:水を蒸発させる
それでは、もう1問問題を解いてみます。
塩化カリウム200gを水500gに加え、加熱して完全に溶かした。この水溶液から一定量の水を蒸発させた後、20℃まで冷却すると塩化カリウムの結晶が149g析出した。蒸発させた水は何gか求めてみましょう。ただし、塩化カリウムの水に対する溶解度は20℃で34,2とします。
飽和溶液かどうかの確認
今回もまず飽和溶液の表をかきたいのですが、この「塩化カリウム200gを水500gに加え加熱して完全に溶かした溶液」は飽和溶液ではないということに注意してください。
なぜなら「塩化カリウムを水に完全に溶かした」としか書いていないので、塩化カリウムを限界まで溶かしたかどうかは分からないからです。
そのためこの状態で表をかくことはできません。
溶質・溶媒・溶液の表を作る
それではどの状態の表を書くべきかというと、この「塩化カリウムの結晶が析出した」とき飽和溶液になったと判断し、このときの表をかきます。
まずは求める蒸発した水の質量をx[g]とおきます。今回求めるxは水なので溶媒となります。この点に注意しながら表をつくっていきます。
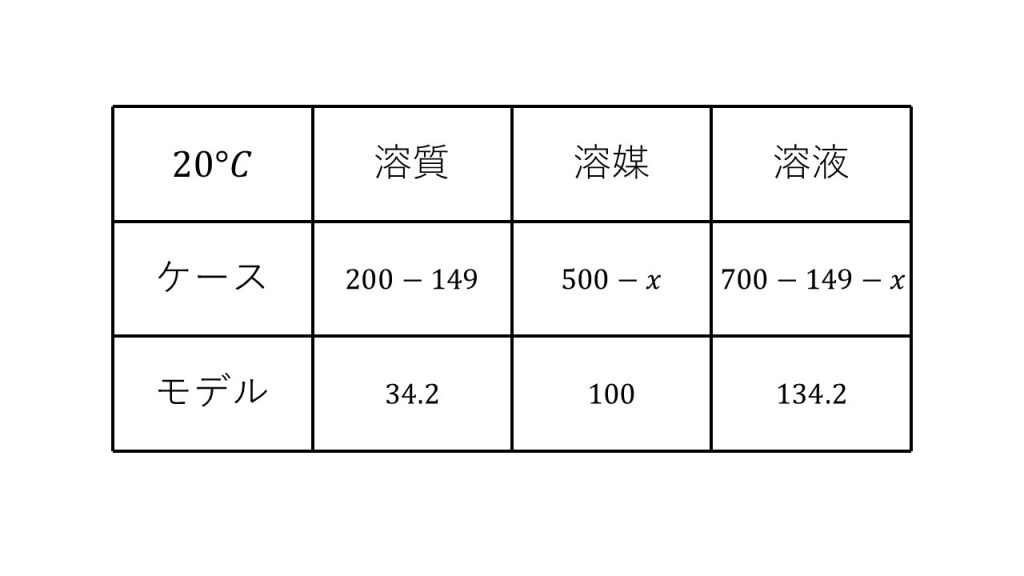
溶解度が34.2なのでモデルの溶質は34.2で、溶媒は100で、溶液は134.2となります。
そして今回のケースにおける溶質は20℃まで冷却したときの溶質なので、もともとあった200gから析出した149gをひいた51gとなります。
次に溶媒ですが、もともとあった500gから蒸発したxgを引いた500-xgとなります。
そして最後に溶液ですが、冷却する前の200+500=700gから析出した溶質の149gを引き、蒸発させた溶媒のxgを引いた700-149-xとなります。
方程式を立てて解く
これでxを含んで溶質、溶媒、溶液の表ができました。
ケースの溶質/モデルの溶質=ケースの溶媒/モデルの溶媒/=ケースの溶液/モデルの溶液となるので、今回は計算しやすい溶質と溶媒を使って方程式をつくります。

それでは方程式を解いていきます。
まずは文字を含む項を左辺に持っていき、それ以外を右辺に持っていきます。そして簡単に約分できるところは約分しておきます。
ちなみに、なぜ51と34.2が3で約分できるか分かるかというと、5+1=6で、3+4+2=9となるから、ともに3で割り切れると分かったのです。このように『各位の和が3の倍数になるときは3で割り切れる』ということは知っておきましょう。
それでは約分をして簡単にしたら右辺を通分します。そして次に、5×11.4は暗算で計算ができるので先に計算をしてしまって、17をひいて2で約分ができるので約分をします。
そして両辺を100倍して左辺の分母をはらって、最後に割り算をして有効数字3桁になるように四捨五入をして、答えは351gとなります。
いかがだったでしょうか。溶解度の計算の基本の流れが理解できたでしょうか。ぜひ自分でも飽和溶液の溶質溶媒溶液の表をつくり、方程式を工夫して解く練習をしてみてください。
(3)解説授業の内容を復習しよう
(4)溶解度の計算の解説
①溶解度の計算の基本(溶質・溶媒・溶液の表を使った計算の方法を解説しています)
②結晶水をもつ固体(硫酸銅(Ⅱ)五水和物)の溶解の計算(硫酸銅(Ⅱ)五水和物の性質についても解説しています)
(5)参考
☆化学の解説動画・授業動画一覧(化学基礎・理論化学・無機化学・有機化学・高分子化合物)
☆化学知識一覧(化学基礎・理論化学・無機化学・有機化学・高分子化合物)
☆化学知識テスト一覧(化学基礎・理論化学・無機化学・有機化学・高分子化合物)
☆化学の解説・授業・知識・演習問題一覧(化学基礎・理論化学・無機化学・有機化学・高分子化合物)
☆化学の語呂合わせ(化学基礎・理論化学・無機化学・有機化学・高分子化合物)
「化学計算の王道」シリーズは『思考訓練の場としての体系化学』(GHS予備校)を参考にしています。
GHS予備校についてはこちら→https://ghs-yobikou.co.jp/
思考訓練シリーズの購入はこちら→https://ghs-yobikou.shop/
