(1)解説授業動画
☆YouTubeチャンネルの登録をよろしくお願いします→大学受験の王道チャンネル
(2)解説授業の原稿
今回は混合気体の計算について解説します。
混合気体の問題を解くときに注意すること
混合気体の計算の問題を解くときに注意すべきことが3つあります。
注意点①:全圧は総粒子数を考える
まず1つ目は、「全圧を考えるときは総粒子数を考える」ということです。
つまり、気体の種類に関係なく、混合気体に含まれている全ての分子の物質量を状態方程式のnに代入するということです。
なぜ全圧を考えるときに、気体の種類に関係なく考えなければいけないのかというと、理想気体であれば、その気体分子がどのような性質を持っているかは考えておらず、混合気体に含まれている気体の分子はすべて同じ粒子である、とみなすことができるからです。
注意点②:分圧の体積とは容器の体積である
2つ目に注意すべきポイントは、「分圧を考えるときの体積は、容器の容積で考えないといけない」ということです。
つまり、状態方程式のVは、その気体が入っている容器の容積であるということになります。
それはなぜかというと、例えば下図の上のように、赤い気体と青い気体の混合気体があったとしたとき、理想気体であれば、この赤い気体の分子と青い気体の分子はぶつかったり、お互いに影響を与えたりすることはないからです。
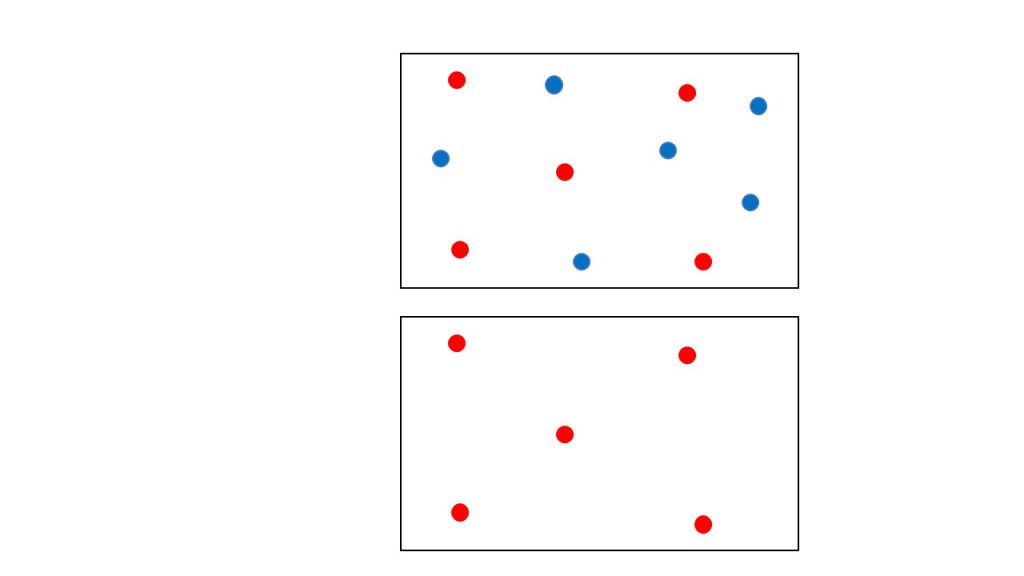
そのため、赤い気体にとって、図の上の状況と図の下の状況は同じ状況であるということが言えます。したがって、赤い気体にとっての体積は、青い気体が含まれていようがいなかろうが容器の容積となるのです。
注意点③:分圧の比は物質量の比
そして、最後に混合気体の計算で注意すべきポイントは、「分圧の比は物質量の比となる」ということです。
これは「気体の圧力は気体分子が壁に衝突することによって生じる」という考え方を知っていれば、理解できると思います。
例えばある壁に気体分子が2粒ぶつかってくるときの圧力をPとすると、ある壁に気体分子が4粒ぶつかってくるときの圧力は、この2倍の2Pとなるように、気体の圧力は粒の数つまり物質量に比例するのです。
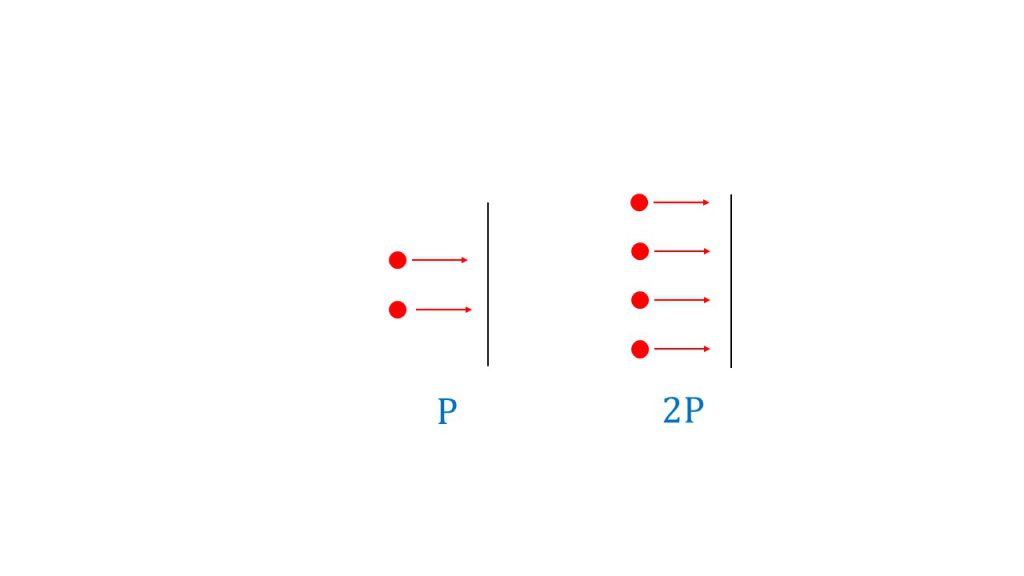
また、このことからドルトンの分圧の法則も理解することができます。ドルトンの分圧の法則とは、「全圧は各成分気体の分圧の合計である」という法則です。

例えば、この混合気体で考えてみると、赤と青の混合気体が壁にぶつかっていく力は、赤の粒が壁にぶつかる力と、青の粒が壁にぶつかる力の合計であるということを表しています。
例題
それではこの3点に注意しながら計算問題を解いてみましょう。
体積4.0Lの容器に、窒素が0.4mol入っています。そして体積2.0Lの容器に酸素が0.3mol入っています。この2つの容器がつながれており、このコックを開けて60℃で放置したとき、この混合気体の全圧と窒素の分圧を求めてみましょう。ただし、気体定数の値は8.3×10³とします。また有効数字は2桁で答えます。

全圧と分圧を求める問題は、全圧を求めてから分圧を求めてもいいですし、分圧を求めてから全圧を求めることもできます。今回は全圧を求めてから分圧を求めてみようと思います。
①全圧を求める
まずは、全圧をP全として状態方程式を立てます。
このとき注意するのが、状態方程式のnの部分は総物質量、つまり窒素の物質量と酸素の物質量を足したものとなります。たとえ混合気体となって窒素と酸素が混ざりあったとしても、それぞれの分子の数の合計は変わることがないので、ここは元の物質量の足し算とすることができます。
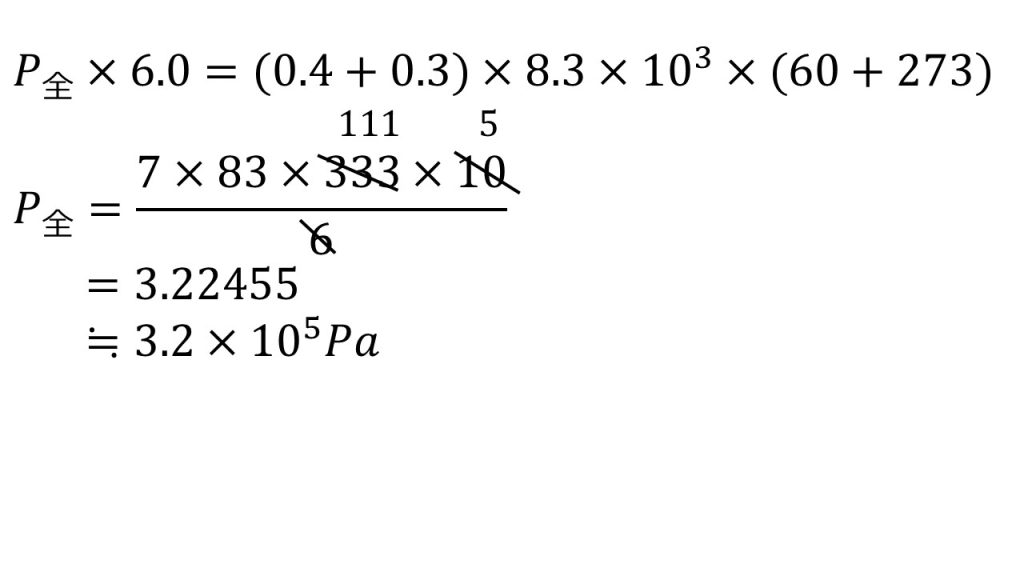
あとは計算をします。
気体定数を含んだ計算は煩雑になりやすいのですが、しっかりと方程式を解くときのルールに従って、なるべく簡単になるようにしましょう。
まずは求めるものを左辺におき、それ以外を右辺に集めます。そして、できるだけ約分をしていきます。約分をしたあとは掛け算をし、最後に割り算をして、有効数字が2桁になるように四捨五入をしたら答えは3.2×10⁵Paとなります。
これで全圧が出ました。
②分圧を求める
続いて窒素の分圧を求めていきます。
窒素の分圧も状態方程式を使って求めることができますが、少し楽に計算するために、ドルトンの分圧の法則を使って窒素の分圧を求めてみようと思います。

ドルトンの分圧の法則つまり「全圧は各成分気体の分圧の合計である」ということと「気体の圧力は物質量に比例する」ということを使うと、窒素の分圧:全圧=0.4mol:0.7 mol=4:7となり、窒素の分圧は全圧を4/7倍したものということになります。
あとは先ほどの全圧を代入して計算していくのですが、ここで注意したいのが、代入するときは、四捨五入した後の値を代入しない方がよいということです。
四捨五入した後の値を代入してしまうと、切り捨てた部分の影響によって計算結果が変わってしまう可能性があるからです。そのため、四捨五入する前の値を代入するようにしましょう。
さらに、掛け算や割り算をする前の分数の状態のものを代入すると計算が楽になることが多いです。今回も分数の状態で代入することで、約分をすることができ、計算が楽になります。
あとは掛け算をして有効数字2桁になるように四捨五入をしたら、答えが1.8×10⁵Paとなります。
ちなみに、どうしても計算した後の値を代入したいときは、有効数字より1つ桁が多い状態(今回で言えば3.22)で代入するようにしましょう。こうすれば計算結果が変わることはほとんどありません。
窒素の分圧を直接求める場合
ちなみに窒素の分圧を状態方程式で求める場合は、以下のようになります。
PN2・6.0=0.4×8.3×103×(60+273)
注意すべきポイントは、体積の部分には容器の全体の容積である6.0Lを使います。ここを4.0としないように注意しましょう。
また窒素の分圧を求めた後、全圧を求める場合は、窒素と混合気体の物質量の比は4:7なので、窒素の分圧に7/4倍することで混合気体の全圧を求めることができます。
P全=PN2×7/4
いかがだったでしょうか。混合気体の計算の基本の考え方が理解できたでしょうか。
混合気体の考え方を理解するためには理想気体とは何か、あるいは気体の圧力とは何かについて理解していないといけません。もし、これらの理解が不十分だと思う場合は、別の動画で詳しく解説しているので、そちらをご覧になってください。
- 理想気体の状態方程式の使い方(理想気体とは何か、混合気体の考え方、計算の工夫の仕方についても解説しています)
- 気体の性質は気体分子で考えることで理解しやすくなります(気体の圧力、混合気体、ドルトンの分圧の法則、気体の運動エネルギー、気体の内部エネルギー、ボイルの法則、シャルルの法則、気液平衡、飽和蒸気圧)
(3)解説授業の内容を復習しよう
(4)理想気体の状態方程式の解説一覧
①気体の性質は気体分子で考えることで理解しやすくなります(気体の圧力、混合気体、ドルトンの分圧の法則、気体の運動エネルギー、気体の内部エネルギー、ボイルの法則、シャルルの法則、気液平衡、飽和蒸気圧)
②理想気体の状態方程式の使い方(理想気体とは何か、混合気体の考え方、計算の工夫の仕方についても解説しています)
③混合気体の計算の基本(全圧・分圧の考え方、ドルトンの分圧の法則についても解説しています)
(5)参考
☆化学の解説動画・授業動画一覧(化学基礎・理論化学・無機化学・有機化学・高分子化合物)
☆化学知識一覧(化学基礎・理論化学・無機化学・有機化学・高分子化合物)
☆化学知識テスト一覧(化学基礎・理論化学・無機化学・有機化学・高分子化合物)
☆化学の解説・授業・知識・演習問題一覧(化学基礎・理論化学・無機化学・有機化学・高分子化合物)
☆化学の語呂合わせ(化学基礎・理論化学・無機化学・有機化学・高分子化合物)
「化学計算の王道」シリーズは『思考訓練の場としての体系化学』(GHS予備校)を参考にしています。
GHS予備校についてはこちら→https://ghs-yobikou.co.jp/
思考訓練シリーズの購入はこちら→https://ghs-yobikou.shop/
