(1)問題
△ABCにおいて、AB=AC=5,BC=√5とする。辺AC上に点DをAD=3となるようにとり、辺BCのB側の延長と△ABDの外接円との交点でBと異なるものをEとする。
①BEを求めよ。
②△ACEの重心をGとする。AGを求めよ。
③ABとDEの交点をPとする。DP:PEを求めよ。
④DE、EPを求めよ。
(2015年センター試験本試験数学ⅠA第6問より)
(2)答案
①
問題演習(2015年センター試験本試験数学ⅠA第6問)1-1024x576.jpg)
②

③

④


(3)解法のポイント
①円と直線が2本交わっていたら、まずは方べきの定理を考えましょう。
②重心の定義(中線の交点)は忘れがちなので注意しておきましょう。
③三角形と直線が交わっていたらメネラウスの定理を考えましょう。
④図形の問題で詰まったら、まずは相似を考えてみてください。相似は中学の学習範囲ですが、それゆえに盲点になりがちです。
(4)必要な知識
①方べきの定理
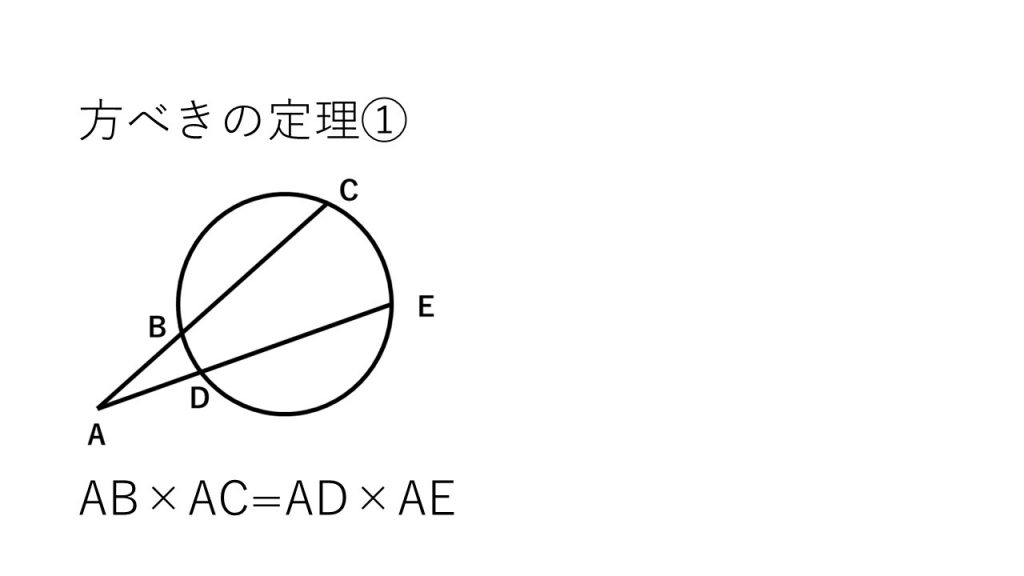
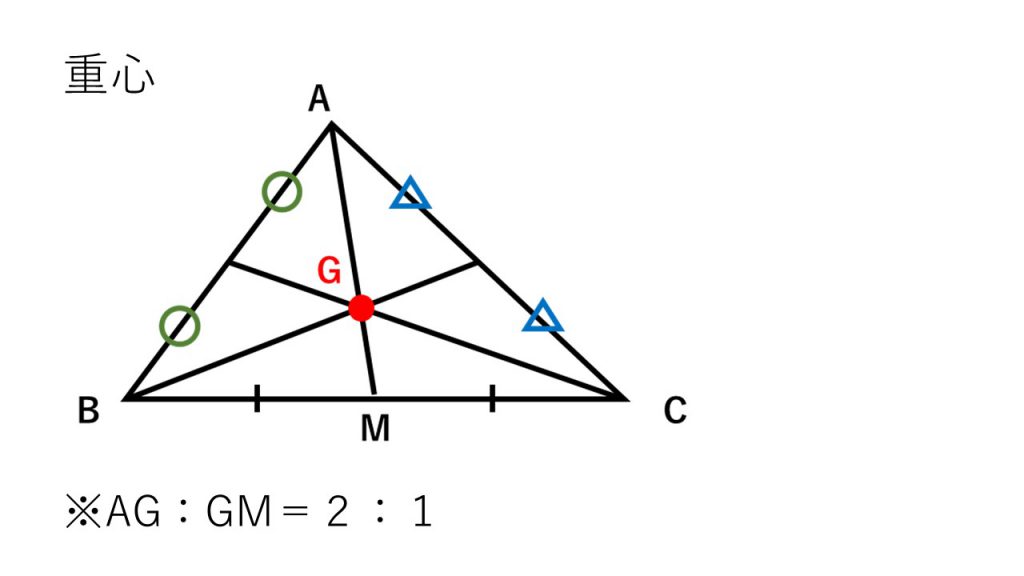
②重心
→定義:中線(三角形の頂点とその対辺の中点を結んだ直線)の交点
③チェバ・メネラウスの定理
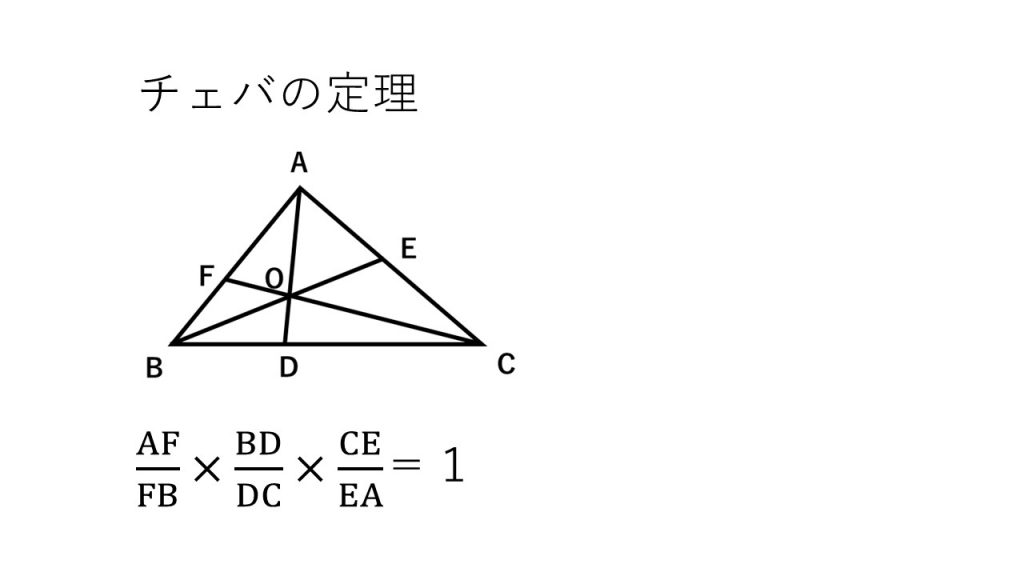
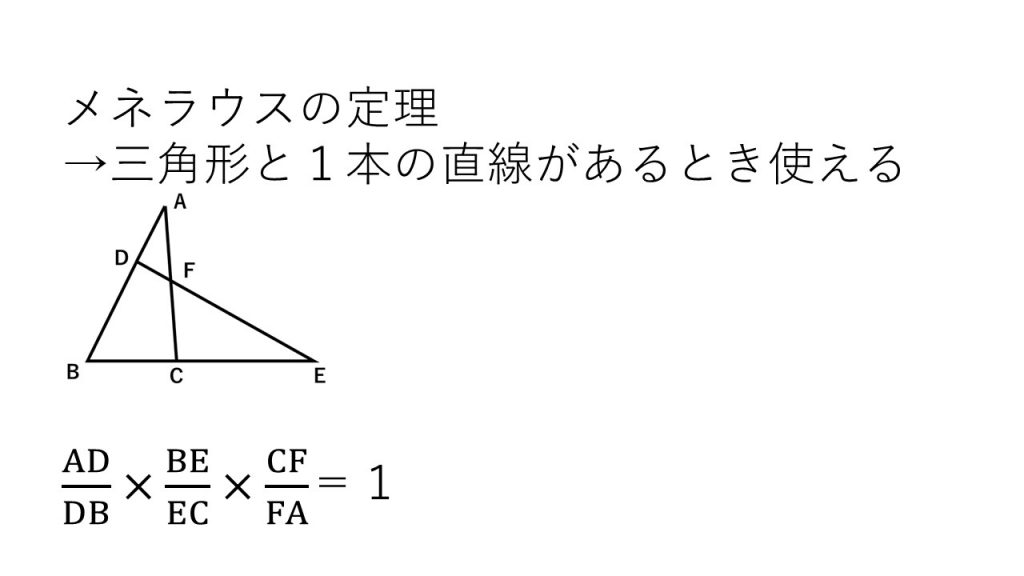
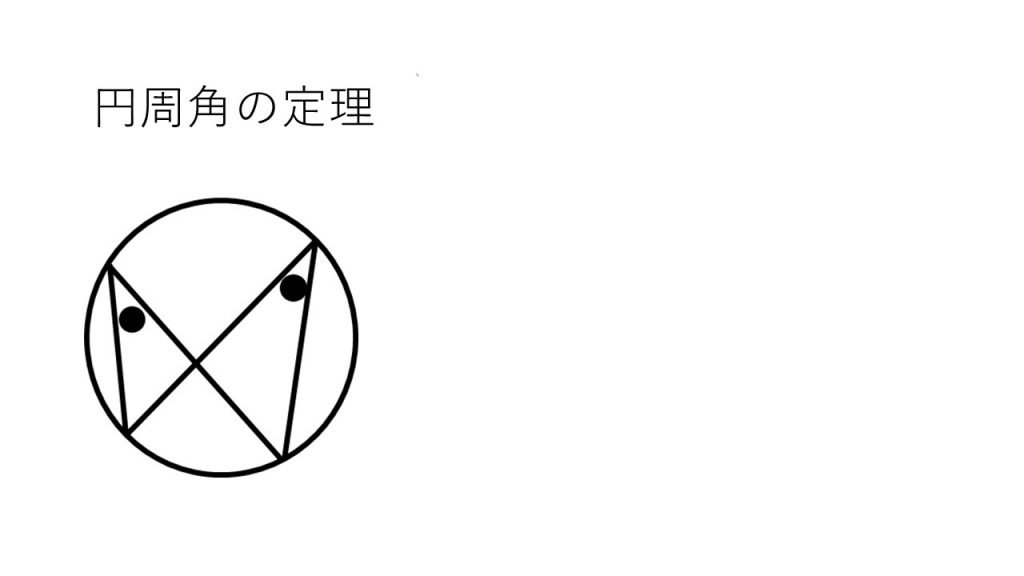
④円周角の定理
(5)理解すべきこと
チェバ・メネラウスの定理の簡単な使い方を知っておきましょう→チェバ・メネラウスの定理の簡単な使い方
☆動画はこちら↓
