(1)解説授業動画
☆YouTubeチャンネルの登録をよろしくお願いします→大学受験の王道チャンネル
(2)解説授業の原稿
電気回路は水路をイメージする
回路の考え方の基本である「回路は水路をイメージする」ということを解説します。
回路は水路をイメージすることで理解しやすくなります。もう少し具体的に言うと電流は水、電源はポンプ、抵抗は下り坂、そして導線は高低差のない水路とイメージします。
例えば、下図の左ような電源と抵抗をつないだ回路があった場合、下図の右のような水路をイメージします。
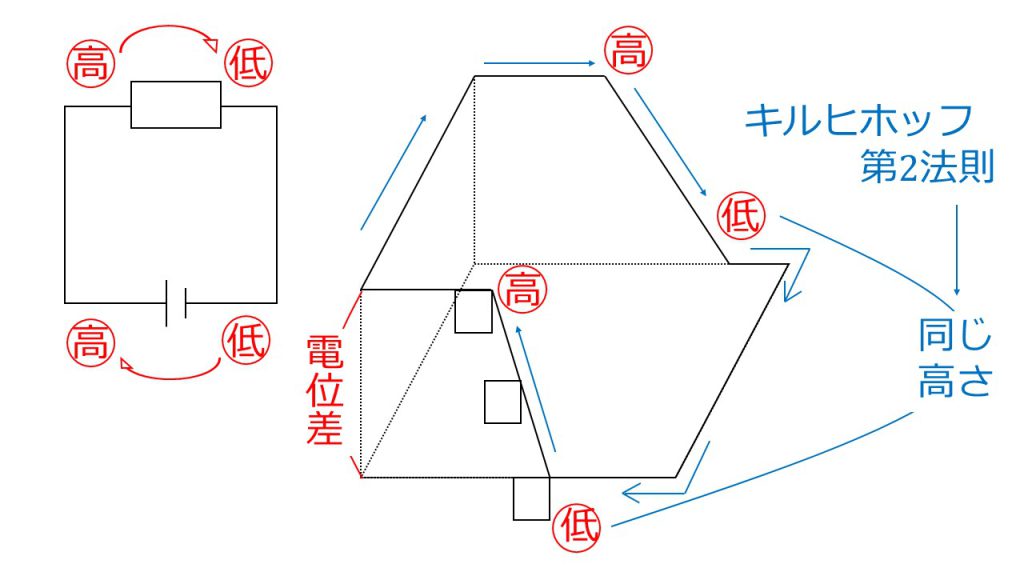
つまり、電源は低い位置から高い位置まで水をくみ上げるポンプをイメージし、導線の部分は高低差のない水路で、抵抗は高い位置から低い位置に水を流す下り坂であるとイメージします。そして、ぐるっと周ってまた元の位置に戻る。このように回路をイメージします。
水路の高さは電位を表している
すると、この水路の高さというものは電位を表しているものということになるので、電源は低電位から高電位に電流を流すはたらきがあるということがわかり、抵抗は高電位から低電位に電流を流すものであるということがわかります。この抵抗の両端で電位つまり電圧が下がっていることを電圧降下といいます。
導線は導線自体の抵抗がないものとすれば高低差がないつまり電位差がないものとして考えるので、電圧降下をすることなく電流が移動します。
このようにして考えてみると、電源によって引き上げた高さと同じ分だけ高さを下げないと回路が成り立たないということがわかります。そして、このことをキルヒホッフの第2の法則というのです。
キルヒホッフの第2法則
それではキルヒホッフの第2法則をもう少し詳しく解説します。
この法則の定義は、「任意の閉回路において起電力の合計は電圧降下の合計に等しい」というものです。
先ほどのイメージで説明すると、水路を形成して水を循環させるためにはポンプによって引き上げた高さと同じ分だけ下り坂によって落とさないといけないということになります。
下図の回路で考えてみましょう。

このように3つある電源の起電力をそれぞれE1, E2,E3とし、4つある抵抗の大きさをそれぞれR1, R2, R3, R4とします。そして、I1, I2の電流の位置と向きを図の通りにします。
「任意の閉回路」というのは、「自分で選んだどの閉回路においても成り立っている」ということです。
閉回路とは閉じた回路、つまりぐるっとまわって元の位置に戻った回路ということになります。今回で言えば、図の①のような閉回路や、②のような閉回路、あるいは③のような閉回路が考えられます。
閉回路①
まずは、閉回路①においては、E1で電圧を引き上げて、さらにE2でも電圧を引き上げます。そしてR1, R2, R3で順番に電圧を落としていき、元の高さに戻らないといけません。そのため以下のような式が成り立ちます。
E1+E2=R1I1+R2I1+R3I1
各抵抗における電圧降下の値は、V=RIつまりオームの法則を使って求めることができます。するとこの①の閉回路においてE1+E2=R1I1+R2I1+R3I1が成り立っているというのがキルヒホッフの第2法則です。
閉回路②
また、②の閉回路では以下の等式が成り立っています。
E1ーE3= R4I2
ポイントは「閉回路を考えている向きに注意する」ということです。
今回、図の矢印の向きで考えているのでE1は正ですがE3は負となります。なぜならE3は矢印の向きとは逆方向に電圧を引き上げているからです。
そして、電圧降下は抵抗が1個しかないのでR4I2のみとなり、上記の式が成り立ちます。
イメージとしてはE1で高さを上げ、E3で高さを落とし、R4でも高さを落とし元の高さに戻っているというイメージになります。
閉回路③
③の閉回路でも考えている回路の向きに注意してください。
E3+E2=R1I1+R2I1+R3I1ーR4I2
今回も図の矢印の向きで考えています。そのため左辺の起電力はE3+E2となります。今回、E3は考えている向きと同じ向きなのでプラスとなります。
そして R1, R2, R3で電圧降下をし、R4は電流の向きが下向きなので逆向きに電圧降下を起こしているのでマイナスとなります。
イメージとしてE3で高さを上げ、E2でも高さを上げ、R1, R2, R3で高さを落とし、R4は上り坂となって元の高さに戻っていくというイメージになります。
このようにキルヒホッフの第2法則を考えるときはどの閉回路を選んでもいいですし、また、向きも自分で決めても構いません。
ただし、自分が決めた向きに対して正なのか負なのかは注意するようにしましょう。起電力であればどちらが低電位でどちらが高電位であるか、あるいは抵抗の電圧降下であれば電流の向きに注意して正負を考えるようにしましょう。
キルヒホッフの第1法則
またついでにキルヒホッフの第1法則についても確認しておきます。
この法則の定義は、「任意の分岐において、流入する電流と流出する電流は等しい」というものです。
例えば、先ほどと同じ回路において、下図の通り、導線を流れる電流をI1, I2, I3とします。

すると、赤丸の分岐点において流入する電流はI1とI2です。そして、この分岐点において流出する電流はI3です。そのため
I1+I2=I3
という等式が成り立ちます。
これは電流を水と考えれば当然のことだと思います。流れ込んできた水の合計がそこから出て行く水の合計と等しくなる、これを表しているのがキルヒホッフの第1法則です。
直列つなぎの合成抵抗
それでは最後に今までの考え方を使って抵抗の合成を考えてみます。
例えば、下図の左のように電源に2つの抵抗が直列でつながれていたとします。
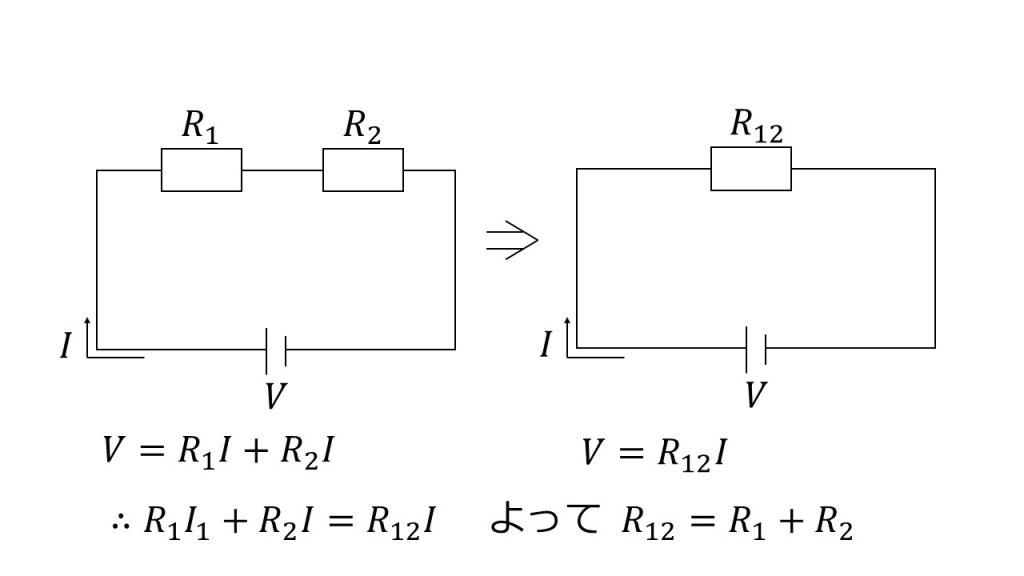
イメージで考えると、電源によって高さを引き上げて、まず1つ目の抵抗で高さを落とし、2つ目の抵抗でさらに高さを落とし、元の高さに戻っていくという回路なのですが、結局のところ元の高さに戻ってくればいいので、この2つの下り坂を合わせて1つの下り坂と考えることができます。このことを抵抗の合成と言います。
キルヒホッフの第2の法則により、この左の回路において「起電力の合計=電圧降下の合計」の等式が立てられます。
V=R1I+R2I
また、右の回路においても同様に式を立てることができます。
V= R12I
よってこの2つの等式からVを消去して両辺をIで割ると合成抵抗を元の抵抗で表すことができます。
R1I+R2I=R12I
∴ R12=R1+R2
抵抗の直列つなぎの場合は足し算になるということは知っておきましょう。
また、R1とR2の合成抵抗は、R12のように書くと分かりやすくなるのでぜひこのように書くようにしてください。
並列つなぎの合成抵抗
また、下図のように抵抗を並列でつないだときの合成も考えてみます。
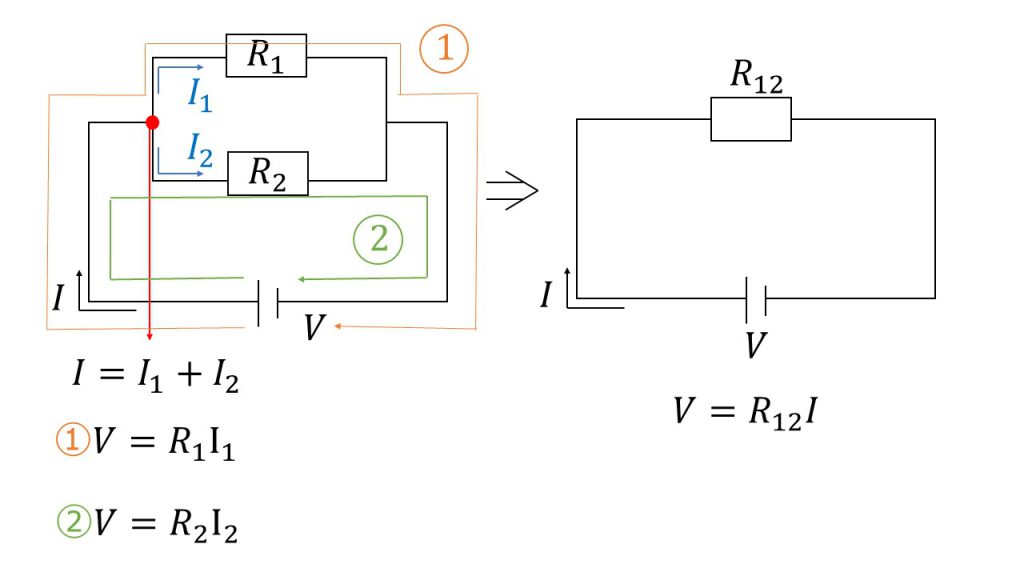
こちらもイメージで考えてみると、電源によって電圧を引き上げ、並列なので2つの水路分かれるのですが、どちらも同じ高さだけ落ちて元の高さに戻っていくという回路になります。途中で枝分かれはしているけれど結局この回路も元の高さに戻ってくるので、この2つの抵抗をまとめて1の抵抗と考えることができます。
この合成はキルヒホッフの第1法則と第2法則の2つを使って考えます。
R1の方に流れる電流をI1、R2の方に流れる電流をI2とすると、赤丸の分岐点においてキルヒホッフ第1の法則が成り立ちます。つまり「流入する電流=流出していく電流の合計」となります。
I= I1+I2
また、閉回路①と閉回路②の2つの閉回路においてキルヒホッフ第2の法則を使って2つの式を立てることができます。
V=R1I1 ⇔ I1=V/R1
V=R2I2 ⇔ I2=V/R2
また、右の回路でも同様にキルヒホッフ第2の法則を使って式を立てます。
V=R12I ⇔ I=V/R12
次にこの3つの式をI=~の形に式変形して、I= I1+I2の式に代入し両辺をVで割ると以下の等式が導かれます。
1/R12=1/R1=1/R2
これが抵抗の並列つなぎにおける合成抵抗の式です。抵抗の並列つなぎの場合は逆数の足し算になっていることに注意してください。
いかがだったでしょうか。回路の考え方の基本が理解できたでしょうか。ぜひ今回の考え方を使ってさまざまな問題に取り組んでみてください。
(3)解説授業の内容を復習しよう
(4)電流(電磁気)の解説一覧
②電流の表し方は3通りあります(電流の定義、自由電子の動きと電流、オームの法則、抵抗とは何か、抵抗率についても解説しています)
③回路は水路をイメージすると理解しやすくなります(キルヒホッフの第1法則、キルヒホッフ第2法則、抵抗の合成についても解説しています)
(5)参考
☆物理の解説動画・授業動画一覧(力学・熱力学・波動・電磁気・原子)
☆物理に関する現象や技術(力学、熱力学、波動、電磁気、原子)
