(1)例題
「『三つの内角がすべて異なる、または直角三角形ではない』ならば『45°の内角は一つもない』」という命題の反例を次から2つ選べ。
①直角二等辺三角形
②内角が30°、45°、105°の三角形
③正三角形
④三辺の長さが、3、4、5の三角形
⑤頂角が45°の二等辺三角形
(センター数ⅠA 2013年本試)
(2)例題の答案
「三つの内角がすべて異なる、または直角三角形ではない」を満たすのは、②③④⑤である。
この4つから「45°の内角は一つもない」を満たしていないもの、つまり「45°の内角が少なくとも一つある」ものを選ぶと、②と⑤であり、これが反例となる。
(3)解法のポイント
pならばqの反例は、pを満たしてはいるがqを満たしてないものをいいます。そのため、解法の手順は、
pを満たすものをピックアップして、qの否定を選ぶ
となります。
①はそもそも「三つの内角がすべて異なる、または直角三角形ではない」を満たしていないので、反例にすらなりません。
また、「45°の内角は一つもない」の否定は、「全ての内角が45°」ではないので注意してください。
(4)必要な知識
①反例の見つけ方
→pならばqの反例:pを満たし、かつ、qを満たさないもの
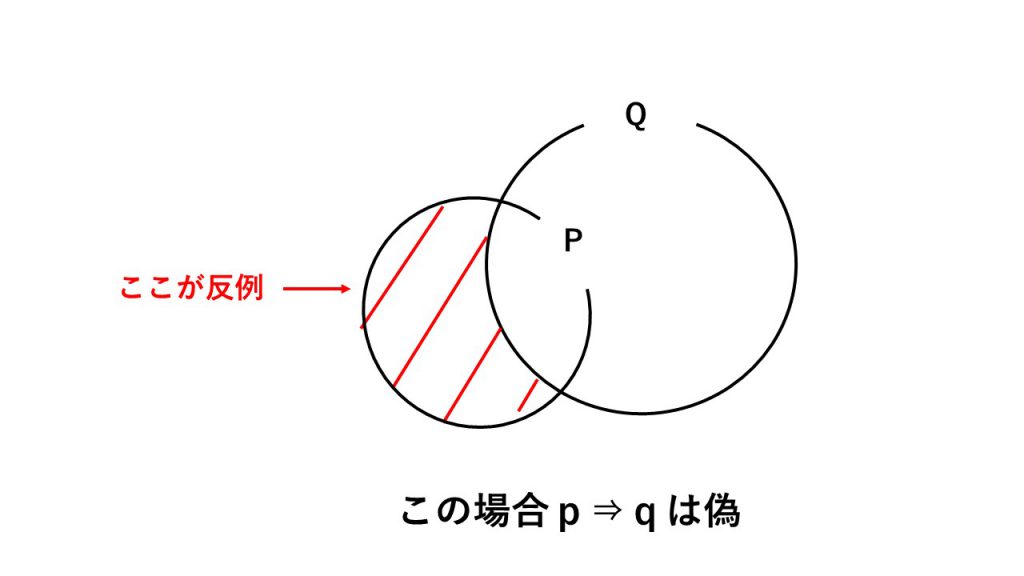
(5)理解すべきこと
命題と集合の関係を理解しましょう→命題の真偽を集合で考えてみましょう!(命題の真偽と集合の関係、「P⇒Qが真」⇔「P⊂Q」)
