(1)例題
(例題作成中)
(2)例題の答案
(答案作成中)
(3)解法のポイント
軸や範囲に文字が含まれていて、二次関数の最大・最小を同時に考える問題です。最大値と最小値の差を問われることが多いです。
最大値だけ、あるいは最小値だけを問われるよりも、場合分けが複雑になります。
ただ、基本は変わらないので、
①定義域
②定義域の中央
③軸
この3つ線を縦に引くことを考えましょう(範囲は両端があるので、線の本数は4本になることがある)
その上で場合分けを考えるわけですが、もし最大値と最小値を同時に考えるのが難しければ、それぞれ別に求めてから後で合わせるといったやり方でもOKです。
もし、最大値と最小値をまとめて求めるための場合分けをするとすれば、以下のようになります。
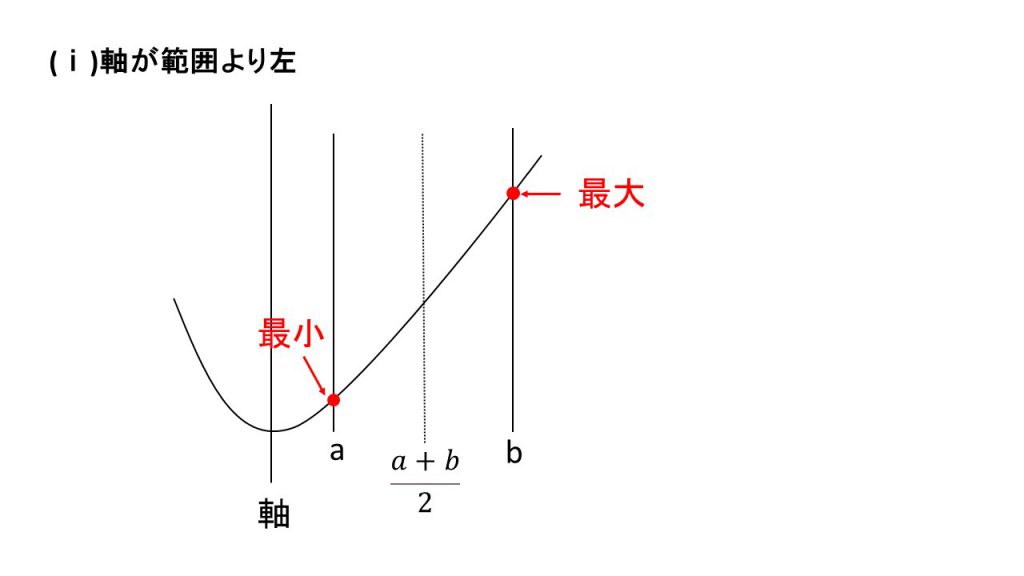
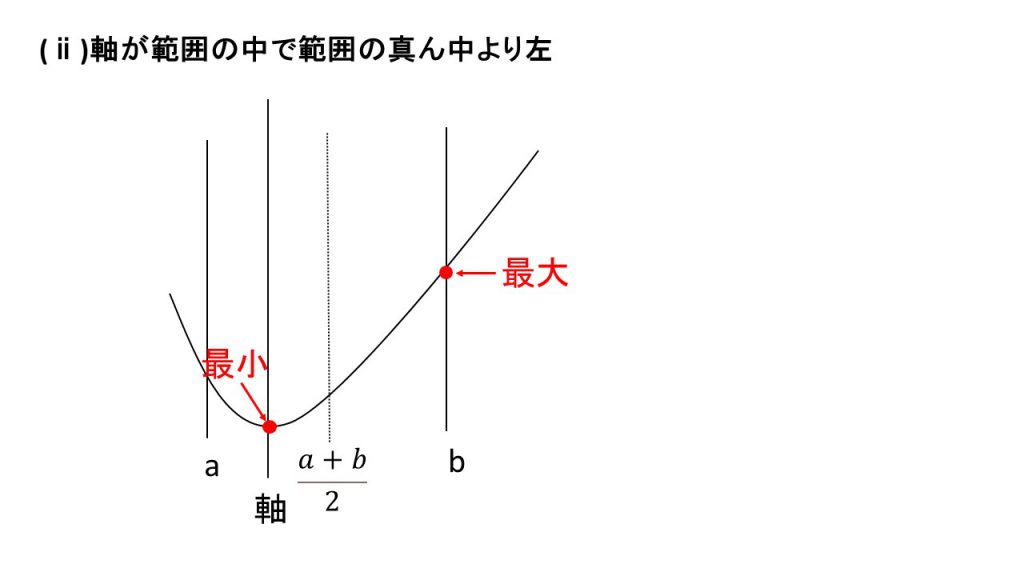
ⅰ)軸が範囲より左、ⅱ)軸が範囲の中で範囲の真ん中より左、ⅲ)軸が範囲の真ん中の線と一致、ⅳ)軸が範囲の中にあり範囲の真ん中より右、ⅴ)軸が範囲より右
の5つの場合分けをすることになります。



(4)理解すべきコア(リンク先に動画があります)
二次関数の最大と最小を考えるときに引くべき3つの線を理解しましょう(場合分けについても解説しています)→二次関数の最大と最小を考えるときに引くべき3つの線
