(1)解説授業動画
☆YouTubeチャンネルの登録をよろしくお願いします→大学受験の王道チャンネル
(2)解説授業の原稿
二次関数の最大と最小を考えるときに引くべき3つの線
二次関数の最大と最小の問題を解くときは、まず、縦に3つの線を引くようにしましょう。縦に引くつの線とは、
①定義域
②定義域の中央
③軸
この3つの線のことです。この3つの線をこの順番で引くようにしましょう。
ちなみに、定義域は両端があることが多いので、線の本数は4本になることが多いです。
具体的に問題で確認してみましょう。
例題1: y=2x2−8x+3 (0≦x≦3)の最大・最小
y=2x2−8x+3 (0≦x≦3)
=2(x-2)2−5
よって、軸は x=2
例えば、このような二次関数の最大と最小を求めてみます。あとで軸の線を引くので、先に平方完成をして軸を求めておきましょう。
それでは、3つの線を縦に引いてみます。
①まずは定義域の線を引きます。
②次に定義域の中央の線を引きます。数学において真ん中を求めるときは、足して2で割るというのが基本です。今回もこの0と3を足して2で割った3/2がこの定義域の中央となります。
③そして、最後に軸を引きます。定義域と定義域の中央との位置関係を意識しながら、軸の線を引いてみます。
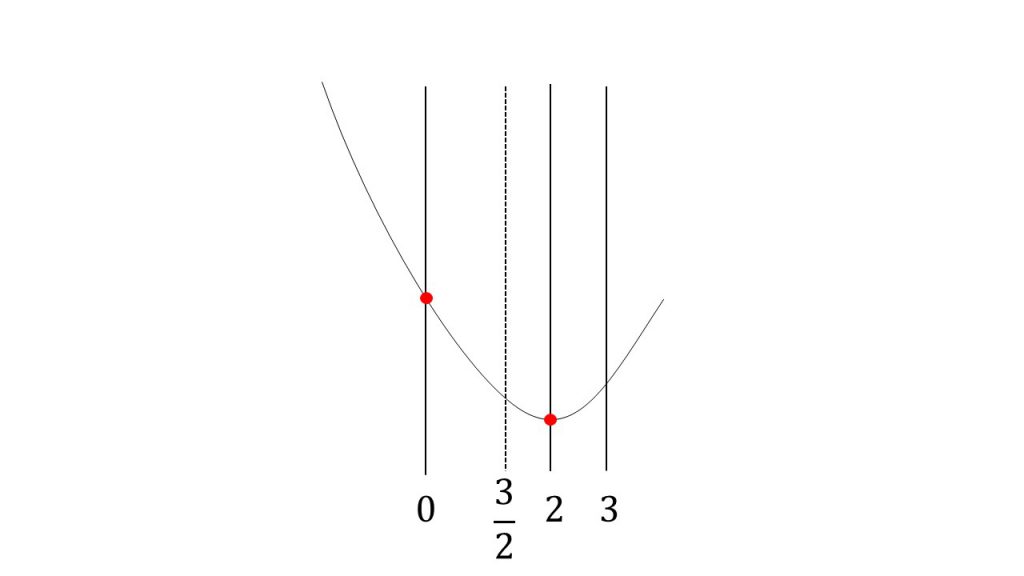
この3つの縦の線を引いたら、あとは上に凸か下に凸かを確認して放物線を書けば、最大値と最小値の位置が分かります。
今回は、この定義域の区間の中で、放物線が一番高くなる場所はx=0のときなので、ここが最大値となり、y=2x2−8x+3の式にx=0代入して最大値は3となり、この区間の中で放物線が一番低くなる場所はx=2のときなので、ここが最小値となり、今度は平方完成された式にx=2を代入して最小値が-5となります。
このよう最大値と最小値を求めるときは、計算が楽になる方に代入するようにしましょう。
例題2:y=x2−2ax+3の0≦x≦4における最小値
それでは、場合分けが発生するタイプの問題でも同様にやってみます。
y=x2−2ax+3の0≦x≦4における最小値を求めよ。
例えばこのような問題があったとします。このように式の中に文字が入っているときは、場合分けが発生します。しかし、基本的な考えは先ほどと同様です。
まずは軸の線を引くので、平方完成をして軸を求めておきます。
y=(x−a)2−a2+3
軸:x=a
そして、先ほどと同様に縦に3つの線を引きます。
①まずは定義域の線を引きます。
②次に、定義域の中央の線を引きます。実は今回は定義域の中央の線は必要ないのですが、一応引いておきます。
③そして、最後に軸の線を引くのですが、今回軸の式に文字が入っています。この場合、軸の位置が確定しないので、場合分けをしなければいけないということに気が付きます。
あとはどのように場合分けをすればよいかですが、それは最小値が変わる軸の位置で場合分けをすることになります。
今回は、
(ⅰ)軸が定義域よりも左側にあるとき
(ⅱ)軸が定義域の中にあるとき
(ⅲ)軸が定義域よりも右側にあるとき
この3つで場合分けをすることになります。
(ⅰ)a<0のとき、つまり、軸が定義域より左側にあるとき、x=0のとき最小となり、y=x2−2ax+3に代入して最小値は3となります。
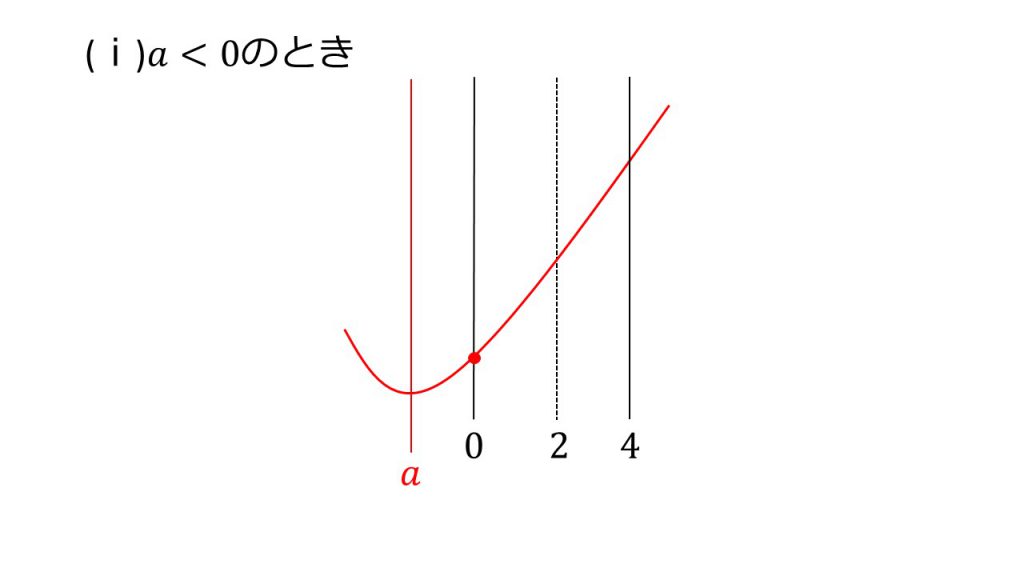
(ⅱ)0≦a≦4のとき、つまり、軸が範囲の中にあるとき、最小値はx=aのときとなり、x=aをy=(x−a)2−a2+3に代入して最小値は −a2+3
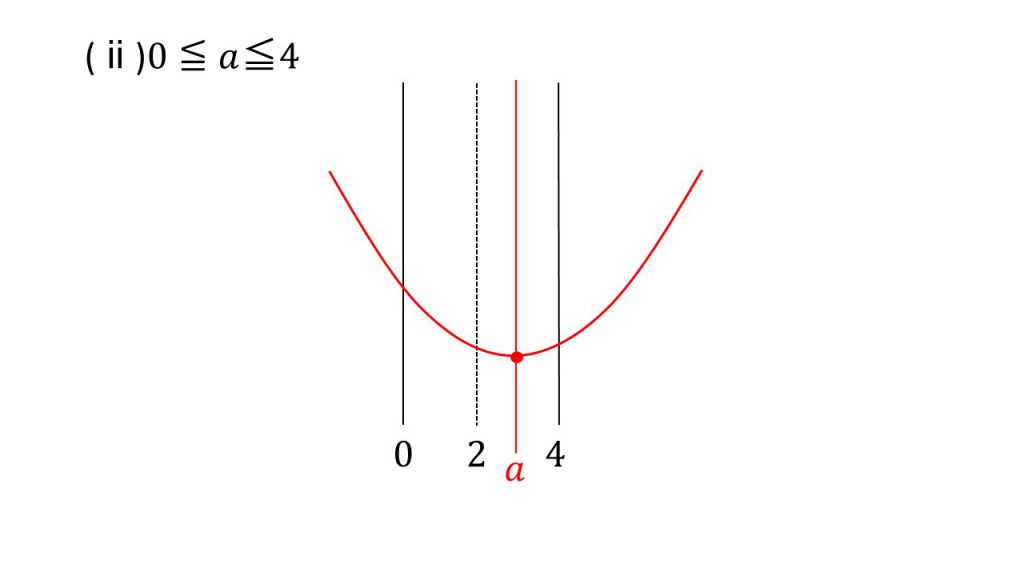
(ⅲ)4<aのとき、つまり、軸が定義域の右側に来るとき、x=4のとき最小値となり、 y=x2−2ax+3に代入して最小値は −8a+19

このように場合分けが必要となるパターンの問題でも、
①定義域、②定義域の中央、③軸
この順番で縦に線を引くことを意識すると、どのように場合分けしていいかが分かるようになります。
例題3:y=−2x2+6x+3のa≦x≦a+1における最小値
次に、このような問題でも同様にやってみます。
y=−2x2+6x+3のa≦x≦a+1における最小値を求めよ。
この問題の場合、定義域に文字が含まれています。このようなときも場合分けが発生するのですが、先ほどと同様に解くことができます。
まずは、平方完成をして軸を求めます。
y=−2(x−3/2)2+15/2
軸:x=3/2
そして同様に、①まずは定義域の線を引き、②次に定義域の中央の線を引きます。このとき、定義域の中央の線の場所は足して2で割ります。すると、a+1/2と求められます。
そして、③軸の線を引くのですが、定義域に文字が含まれているので今回も軸の線の位置が確定しません。そのため先ほどと同様に、最小値の位置が変わる軸の場所で場合分けをします。今回、場合分けの境目は定義域の中央になります。
(ⅰ)軸が定義域の中央よりも左側にあるとき(3/2<a+1/2つまり1<aのとき)は、x=a+1のとき最小値となり、y=−2x2+6x+3に代入して最小値 −2a2+2a+7

(ⅱ)区間の中央と軸が同じ位置にあるとき(a+1/2=3/2つまりa=1のとき)、a+1/2=3/2を解くとa=1となるので、この場合のときに最小となるのは、x=aつまりx=1のときと、x=a+1つまりx=2のときが最小となり、x=1をy=−2x2+6x+3に代入して最小値7

(ⅲ)そして軸が定義域の右側にあるとき(a+1/2<3/2つまりa<1のとき)、x=aのとき最小値となり、y=−2x2+6x+3にx=aを代入して最小値 −2a2+6a+3
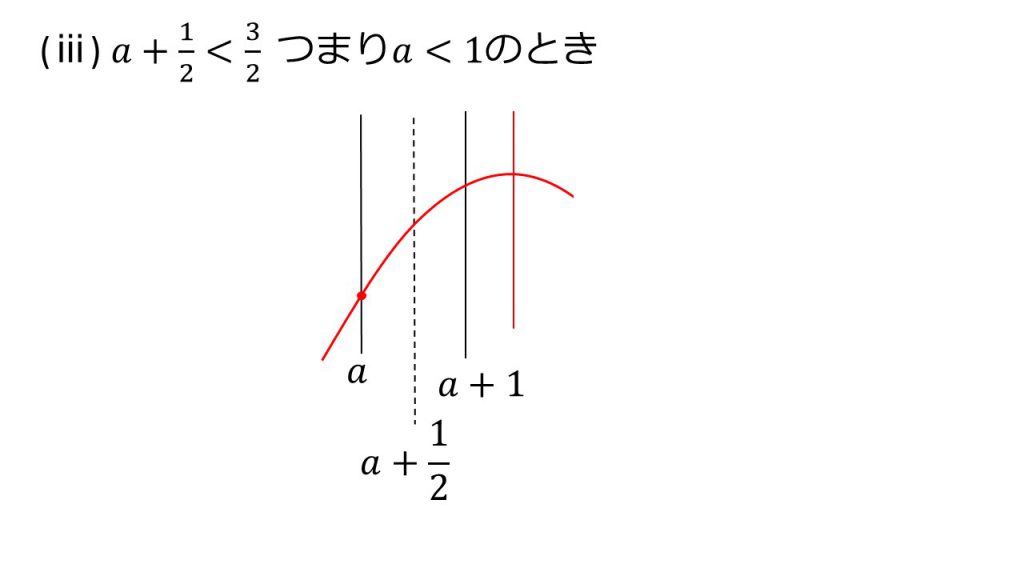
二次関数の最大と最小を考えるときは、場合分けがあろうがなかろうが、まず、
①定義域
②定義域の中央
③軸
この3つの線を縦に引くことから始めてみましょう。
(3)解説授業の内容を復習しよう
(4)二次関数・二次方程式・二次不等式(数学Ⅰ)の解説一覧
②そもそも判別式とは何か(二次関数の問題で判別式を使うときの注意点)
③二次関数の最大と最小を考えるときに引くべき3つの線(場合分けについても解説しています)
⑤二次不等式の解法(解が特殊になる二次不等式の解説もしています)
(5)参考
☆二次関数・二次方程式・二次不等式(数学Ⅰ)の解説・授業・公式・演習問題一覧
