(1)問題

(2012年度センター試験本試数学ⅡB第1問〔2〕より)
(2)答案
①
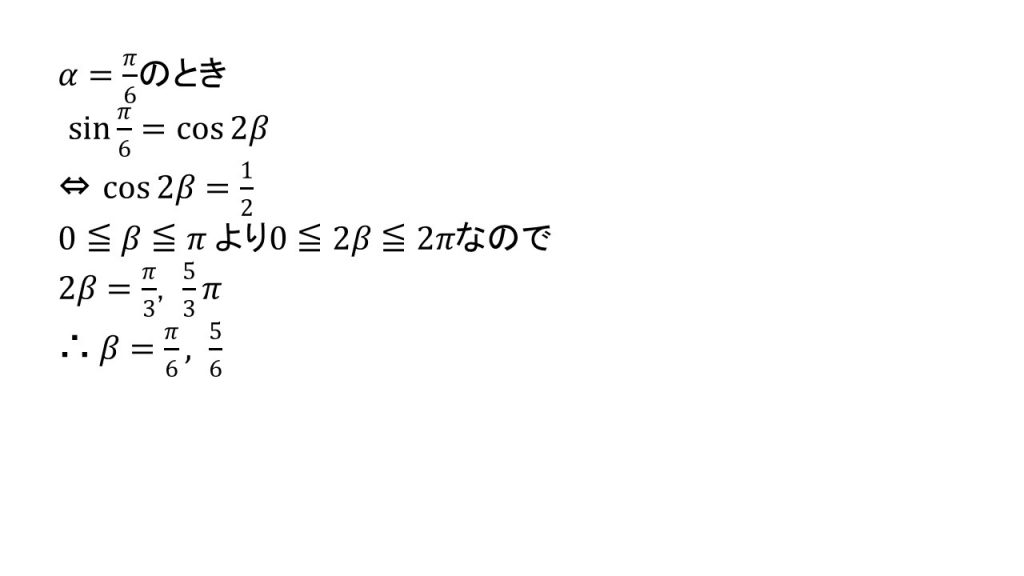

②




③
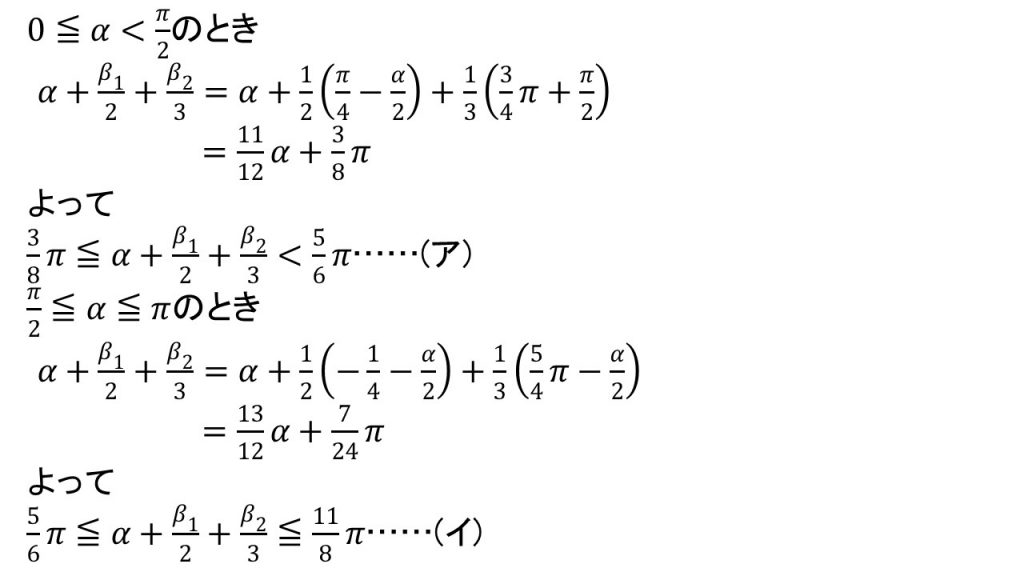


(3)解法のポイント
とにかく三角方程式の解法の5ステップを守れるかどうかがポイントです。こういった応用問題こそ基本通りに解くことが重要です。
①まずは形を整え(cosを左辺に持って来る)→2βの範囲を出し→単位円をかき、範囲を単位円で確認し→x=1/2の線を引く→そして単位円と線の交点からβの方程式を作る
②まずは形を整え(sinをcosに変える、cosを左辺に持って来る)→2βの範囲を出し→単位円をかき、範囲を単位円で確認し→x=cos(π/2-α)の線を引く→そして単位円と線の交点からβの方程式を作る
③形は最初から整っているので→α+β1/2+β2/3の範囲を出し→円をかき、範囲を単位円で確認し→最大値となるy=1の線を引く→そして単位円と線の交点からαの方程式を作る
①~③全て、基本の5ステップになっています。
①と②で、「cosを左辺に持って来る」「2βの範囲を出す」この2つは重要です。①と②においてはβを求めることが目的なので、βを含む式は左辺に持っていき、αは定数扱いとします。
②の「sinをcosに変える」部分はなかなか発想が難しいと思います。「あくまでβを求める問題であるので、cosに形をそろえる」という考えが発想の元となります。
また、π/2-αは0≦α<π/2においては正の鋭角、π/2≦α≦πにおいては負の鋭角であることに注意しましょう。線を引くときは、あくまでαは定数とします。分かりにくいときはπ/3とか2π/3などとして考えてみるとよいでしょう。
(4)必要な知識
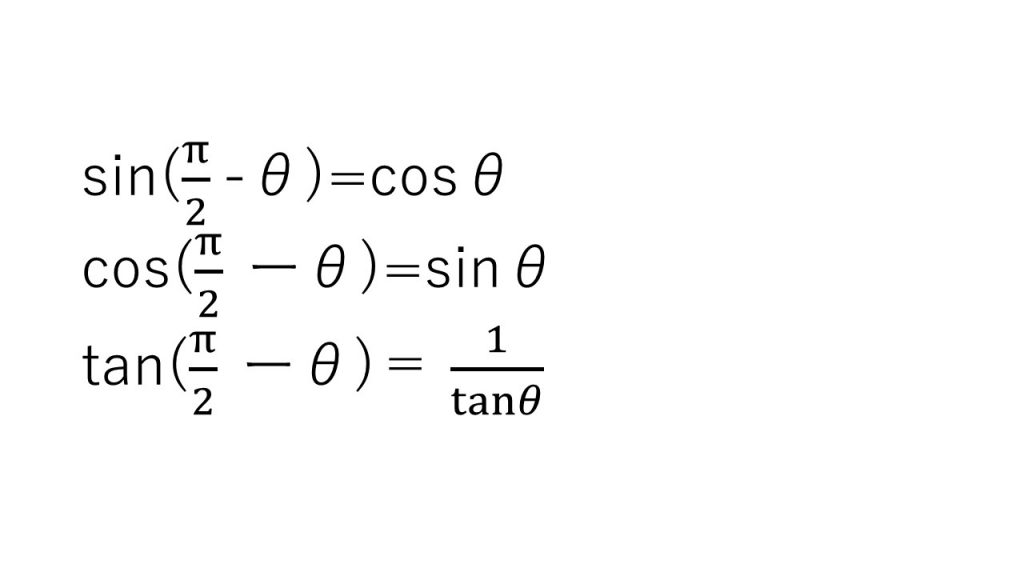
(5)解説授業動画
