(1)例題
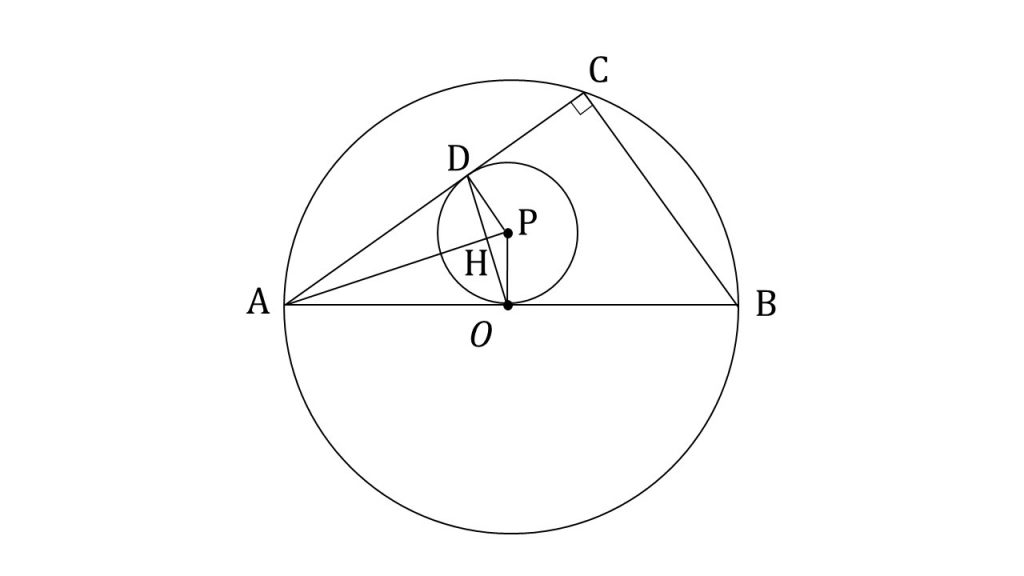
点Oを中心とする半径3の円Oと、点Oを通り、点Pを中心とする半径1の円Pを考える。円Pの点Oにおける接線と円Oとの交点をA, Bとする。また、円Oの周上に、点Bと異なる点Cを、弦ACが円Pに接するようにとる。弦ACと円Pの接点をDとする。
①APの長さとODの長さを求めよ。
②cos∠OADと、ACの長さを求めよ。
③△ABCの面積を求めよ。また、△ABCの内接円の半径を求めよ。
(2013年センター試験本試数学ⅠA第3問より)
(2)例題の答案
①


②

③


(3)解法のポイント
①図形を扱った問題で、詰まったらまず相似を考えてみてください。相似は中学の学習範囲なのですが、それゆえに盲点となることが多いです。
②③直角三角形ができたときは、正弦定理・余弦定理を使うよりも
底辺=斜辺×cosθ
高さ=斜辺×sinθ
高さ=底辺×tanθ
を利用しましょう。その方が早くてラクです。
(4)必要な知識
①直角三角形と三角比

②三角比の相互関係の3つの式

③余弦定理

④三角形の面積の公式2つ

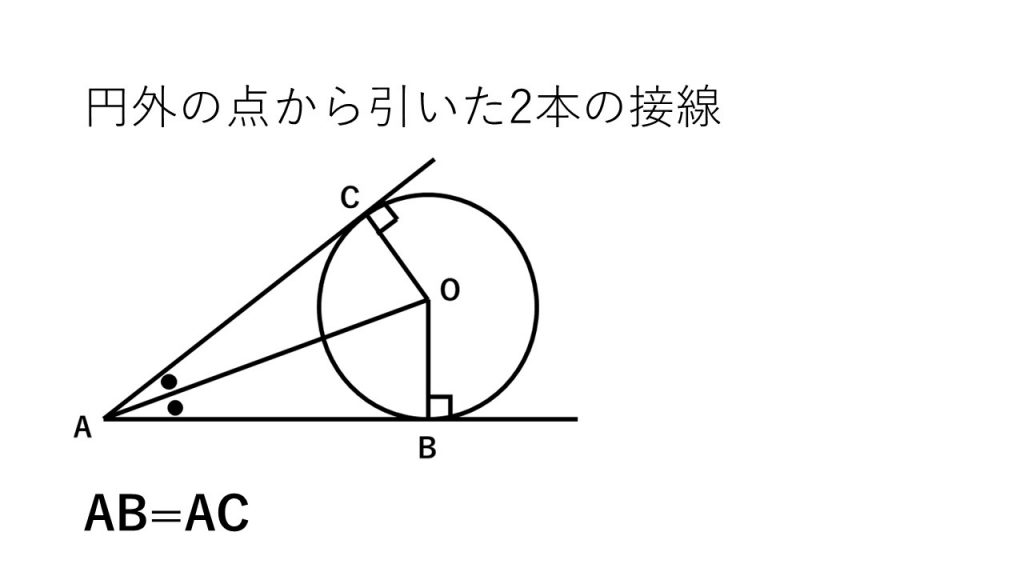
⑤円外の点から引いた2本の接線