(1)解説授業動画
☆YouTubeチャンネルの登録をよろしくお願いします→大学受験の王道チャンネル
(2)解説授業の原稿
ガウスの法則の使いどころについて解説します。
ガウスの法則という名前を聞いたことがあるけど、どこでどのように使えばよいか分からないという方が多いと思います。今回の解説でガウスの法則をどういった問題でどのように使えばよいかを学びましょう。
電気力線とは何か
ガウスの法則は、電気力線に関する法則なので、まずそもそも電気力線とは何か、そして電気力線と電場との関係を確認します。
電気力線とは、下図のように正電荷から出で負電荷に吸収されていく線のことです。つまり、電場の様子を矢印で表したものが電気力線といえます。

矢印の向きが電場の向きを表しており、例えば、正電荷を置いたら、その正電荷は電気力線の向きに電場からの力を受けます。あるいは、負電荷であれば、電気力線の向きとは逆向きの力を受けることになります。このように、電気力線はまずその矢印の向きによって電場の向きを表しています。
電気力線と電場の関係
また、電気力線と電場には、
E=N/S
の関係式が成り立っています。この式のE[N/C]は電場の大きさを表しており、この式のSは面積[m2]を表しています。そして、この式のNが電気力線の本数[本]を表しています。
この式が意味していることは、電気力線の本数を面積で割ったものが電場の大きさになっている、つまり、単位面積当たりの電気力線の本数が電場の大きさであるということになります。
例えば、電気力線が集まって密になっている部分は電場が大きいということを意味しており、電気力線の密度が小さく疎になっている部分は電場は小さいということを意味しているのです。
以上のように、電気力線とは電場の向きと電場の大きさを矢印によって視覚的に分かりやすくしたものということになります。
ガウスの法則の2つのポイント
それでは電気力線とは何かについて確認できたところで、ガウスの法則について確認します。ガウスの法則において重要なポイントが2つあります。
①まず1つ目は、+Qの電荷を帯びているものは、その形状にかかわらず、4πkQ本の電気力線が出ているということです。ちなみに、このkはクーロンの法則の比例定数です。
②また、2つ目のポイントは、電気力線は交わらないということです。
この2つのポイントを押さえておけば、ガウスの法則を使いこなすことができます。
①+Qの電荷を帯びているものは、その形状にかかわらず、4πkQ本の電気力線が出ている
まず1つ目のポイントで大切なことは、形状にかかわらず4πkQ本の電気力線が出るということです。つまり、+Qの電荷を帯びていれば、どんな形であっても、そこから出る電気力線の本数は4πkQ本になるということです。
例えば、下図のような金属球が+Qの電荷を帯びたとしたら、この金属球から出る電気力線の本数は4πkQ本となります。

また、下図のような導体棒が+Qの電荷を帯びたとしても、この棒から出る電気力線の本数はやはり4πkQ本となるということになります。
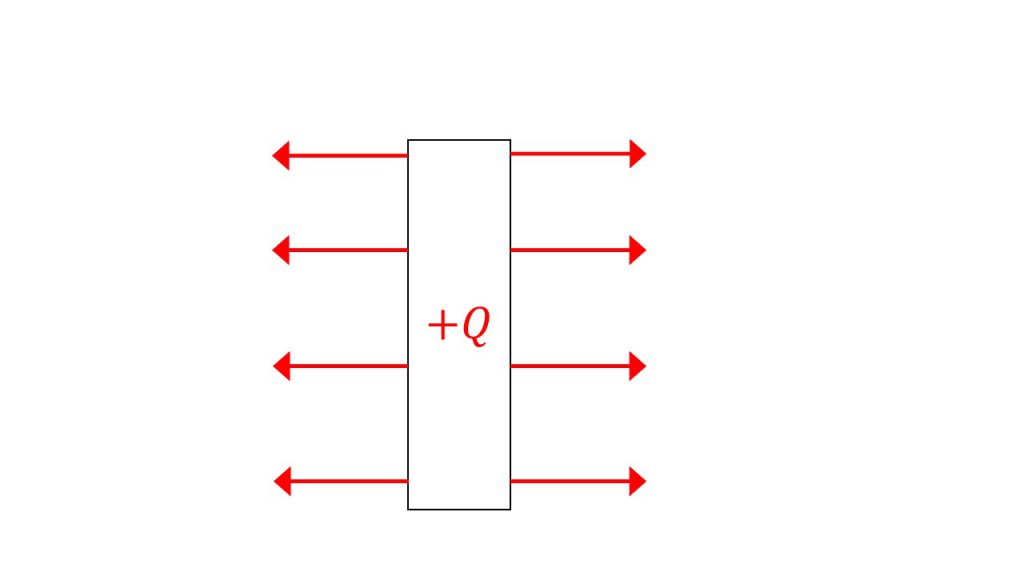
ちなみに、下図のように半径が小さくなったとしても帯びている電荷が+Qであるのならば、そこから出る電気力線の本数は変わらず4πkQ本になります。
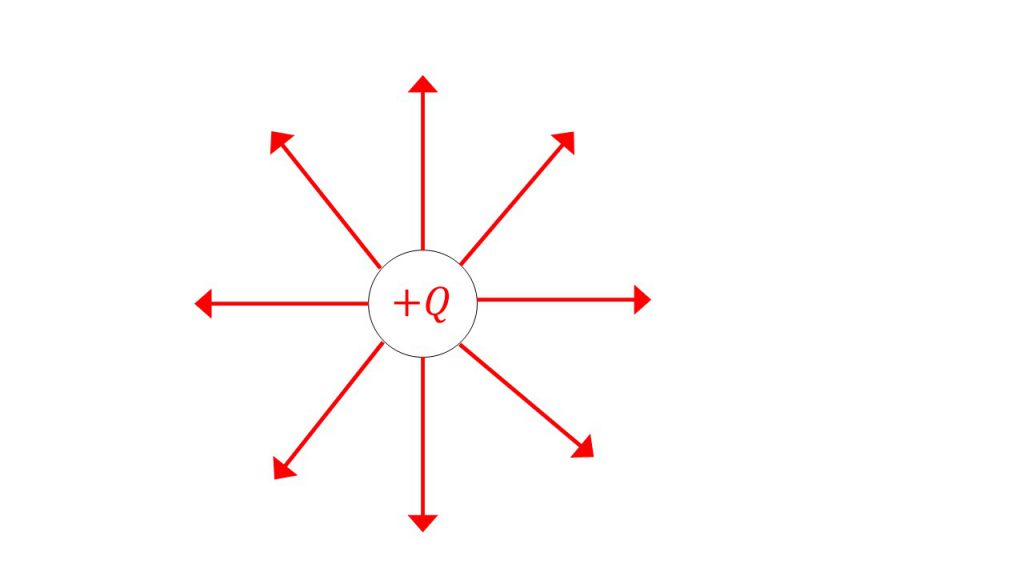
これが1つ目のポイントでいっていることです。
②電気力線は交わらない
そして、2つ目のポイントは電気力線は交わらないということです。そのため、球状のものから電気力線が出る場合は交わらないように出ないといけないので、下図のように中心から放射状に広がるように電気力線が出ます。なぜなら、そうしないと電気力線が交わってしまうからです。
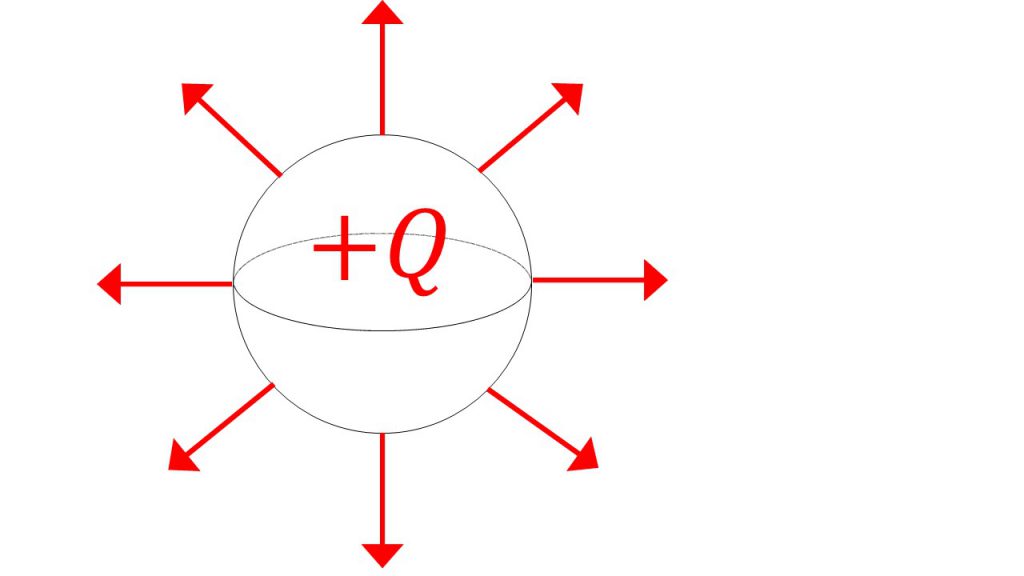
また、棒状のものから電気力線が出る場合は、平行に広がっていきます。こちらも平行に広がっていかないと電気力線同士が交わってしまうからです。
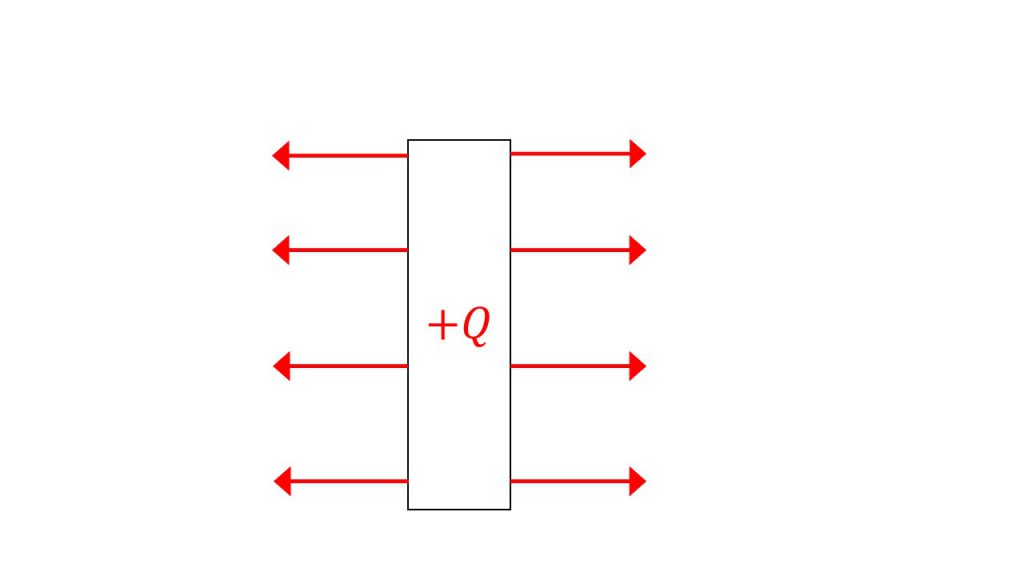
この2つのことから、ガウスの法則は、点電荷ではない、形を持った導体がつくる電場を考えるときに使うものであるということが分かります。これがガウスの法則の使いどころとなります。
金属球が作る電場
それでは、これらを踏まえて金属球、金属板、導体棒が作る電場について考えてみます。それではまず、金属球が作る電場を考えてみます。
例えば、下図のように+Qの電荷を帯びている半径がRの金属球があったとします。

この金属球の中心からr離れた位置の電場の大きさを考えてみます。
先程も確認したとおり、+Qの電荷を帯びた金属球からは球の中心から放射状に電気力線が広がり、その電気力線の本数は4πkQ本となります。
また最初に確認したとおり、電場の大きさは単位面積当たりの電気力線の本数となります。よって、金属球の中心からr離れた位置の電場の大きさを知りたければ、この位置における単位面積当たりの電気力線の本数を求めればよいということになります。
電気力線の総本数を半径rの球の表面積で割る
今回、電気力線の総本数は4πkQ本となっているので、あとは面積で割れば電場の大きさを求めることができます。今回求めるべき面積は、半径rの球の表面積となります。
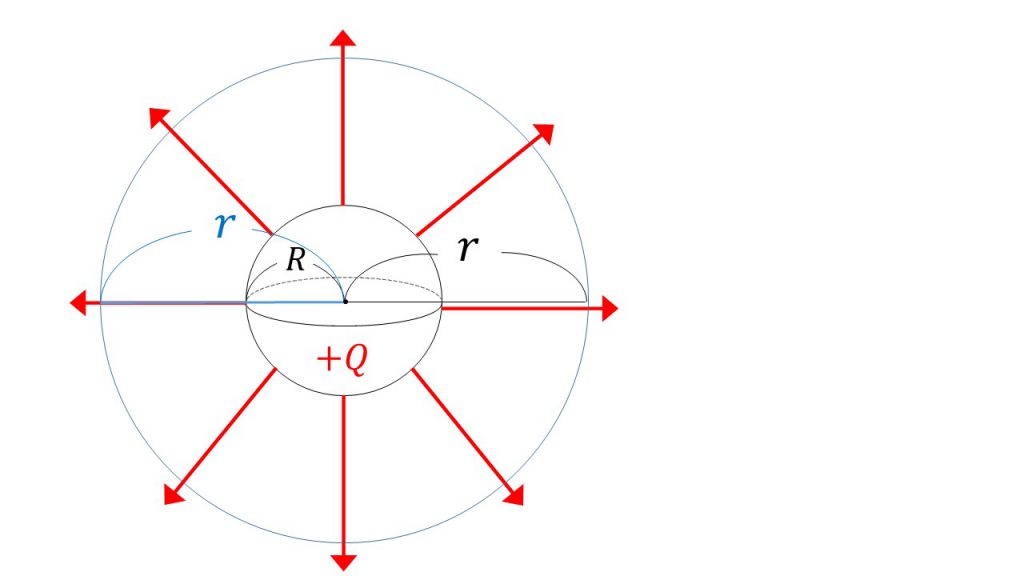
なぜなら、電気力線は金属球から放射状に均等に広がっていくため、この半径rの球の表面上であればどこでも電場の様子が同じになるからです。
つまり、この半径rの球面上であればどこでも電気力線の密度つまり電場の大きさは等しくなるので、求める電場の大きさは、半径rの球の表面を貫く電気力線の本数4πkQ本を、半径rの球の表面積である4πr2で割って、約分をしてkQ/r2となります。
E=4πkQ/4πr2=kQ/r2
このように、ある位置の電場の大きさを求めたいときは、その場所と電場の様子が同じになる図形を考え、その図形の表面を貫く電気力線の本数を数え、その図形の表面積で割ると電場の大きさを求めることができます。
電場の大きさは金属球の半径に関係がない
ちなみに、このE=kQ/r2の式にはRという文字が入っていません。それはつまり、電場の大きさは金属球の半径に関係がないということになります。
よって半径が小さな球であっても、半径が大きな球であっても、帯びている電気量がQであれば、電場の大きさは変わることがなく、kQ/r2となるということになります。
さらに言えば、電荷を帯びている金属球を電荷を帯びていない金属球の中に入れたとしても同様です。
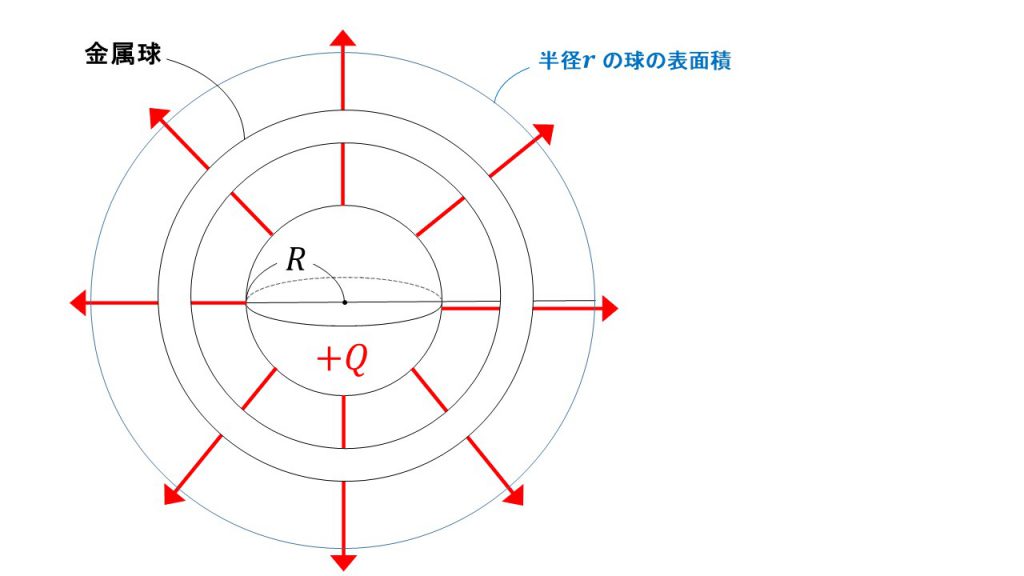
確かに金属球の内部の電場は0になります。しかし、その外側ではやはり4πkQ本の電気力線が出ているので、結局のところ電場の大きさはkQ/r2となります。
金属板が作る電場
次に、金属板が作る電場を考えてみます。
例えば、下図のように面積がSで厚さを無視できる金属板に+Qの電荷を与えたとしましょう。このとき、金属板からの距離がrの位置の電場の大きさを求めてみます。

金属板の場合、電気力線の出方は図のようになります。厚さを無視しているので横からは出ずに、上下に広がっていきます。そして、電気力線は交わってはいけないので、それぞれ平行にまっすぐ伸びていきます。
帯びている電気量は+Qなので、電気力線の総本数は4πkQ本です。よって、上側に伸びている電気力線の本数は2πkQ本で、下側に伸びている電気力線の本数は2πkQ本となります。
電気力線の総本数の半分を金属板の面積で割る
今回はこの金属板と同じ形の図形上であればどこでも電場の様子が同じになります。
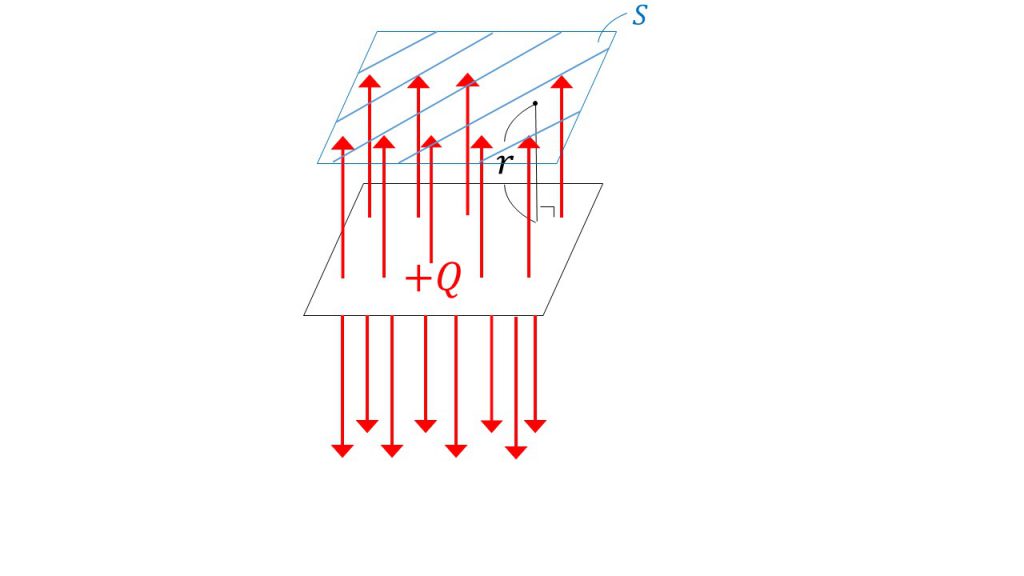
なぜなら金属版の上側から電気力線はまっすぐそれぞれ平行に伸びているからです。
そのため、金属板からr離れた場所の電場の大きさを求めるために考えるべき電気力線の本数は2πkQ本となります。そして、分母の面積は金属板の面積と同じSになります。よって、求める電場の大きさは
E=2πkQ/S
となります。
電場の大きさは金属板からの距離に関係ない
ちなみに、この式にはrという文字が入っていません。
それは金属板から出る電気力線は金属板に対して垂直にまっすぐ伸びていくので、電場の大きさは金属板からの距離によらないということを意味しています。
導体棒が作る電場
それでは最後に、導体棒が作る電場を考えてみます。
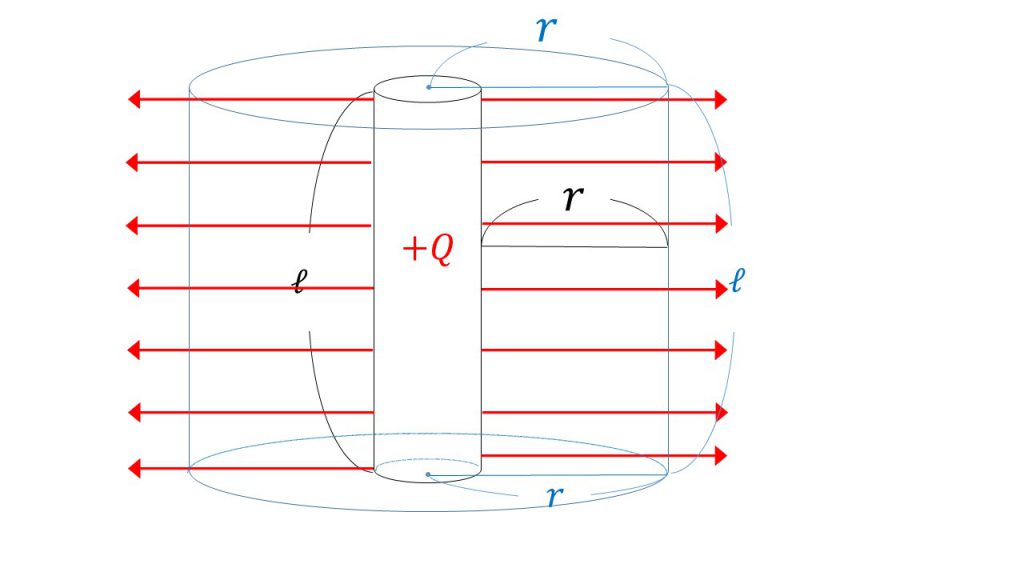
下図のように長さがℓで細い導体棒に+Qの電荷を与えたとします。このとき、導体棒からr離れた位置の電場の大きさを考えてみます。

導体棒の場合、電気力線は図のように広がっていきます。太さを無視しているので上下には電気力線は出ずに、横にそれぞれ平行に広がっていきます。
ただし、正面にも奥にも斜めにも電気力線は伸びていることに注意してください。そのため、この導体棒を上から見ると下図のように円形に電気力線は広がっています。
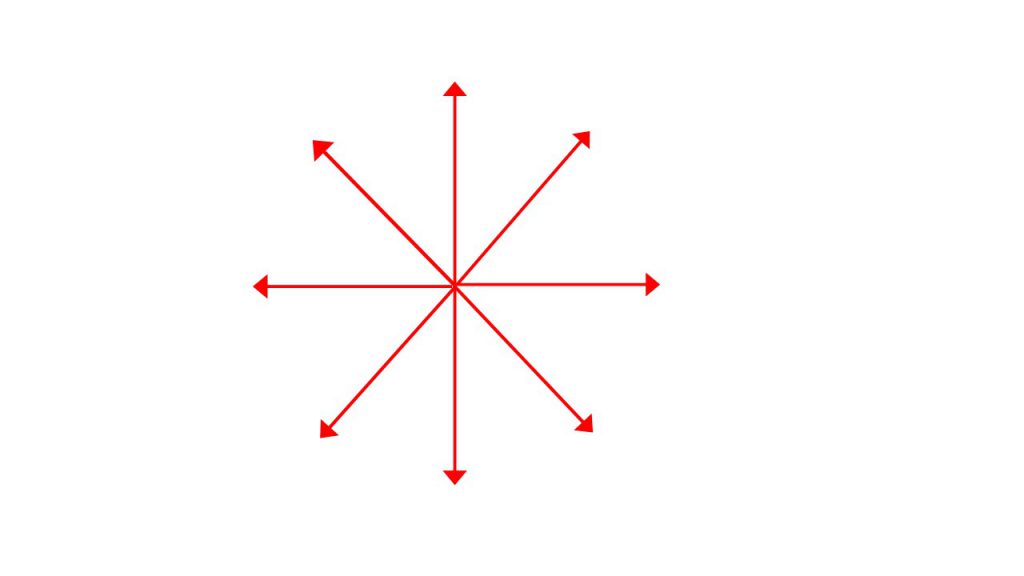
そして、やはり電気力線の本数は電気量が+Qなので4πkQ本となります。
電気力線の総本数を半径r高さℓの円柱の側面積で割る
今回、考えるべき面積は下図のような半径がrの円柱の側面積となります。
円柱を真上から見た図↓
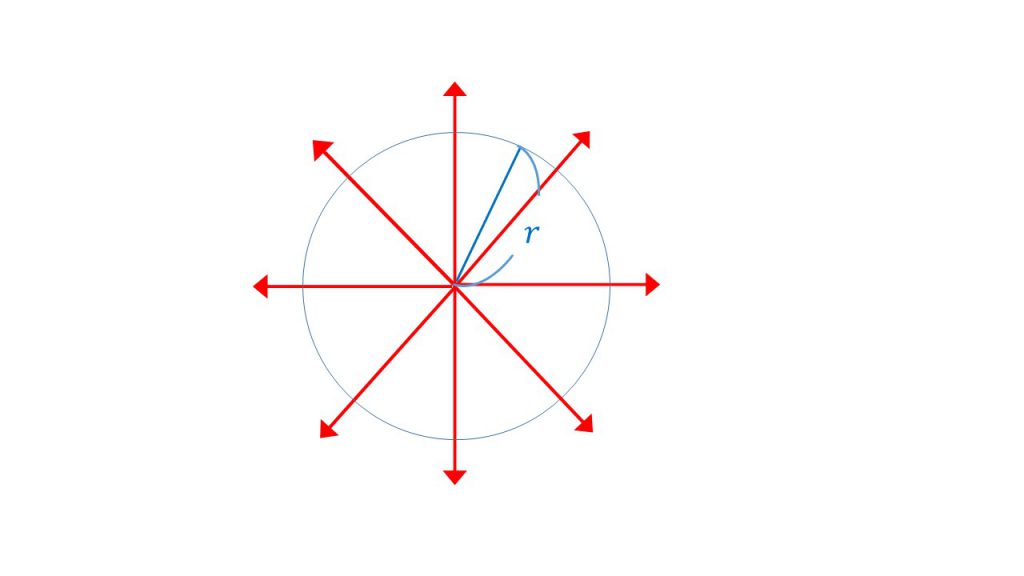
なせなら、今回電気力線は導体棒を中心に円形に均等に広がっているので、半径がr、高さがℓの円柱の側面上であれば、どこでも電場の様子が同じになるからです。
この円柱の側面積は半径がrで高さがℓなので、2πr×ℓとなり、この位置の電場の大きさは、この円柱の側面を貫く電気力線の本数が4πkQ本で、それを側面積の2πrℓで割り、約分をすると求める電場の大きさは2kQ/rℓとなります。
E=4πkQ/2πrℓ=2kQ/rℓ
いかがだったでしょうか。ガウスの法則はこのように電場を図形的に考えるときに使います。基本的には今回ご紹介した金属球や金属板や導体棒が作る電場を問われることが多いので、ぜひ今回の解説が理解できるようになるまで復習してください。
(3)解説授業の内容を復習しよう
問題作成中
(4)電場と電位(電磁気)の解説一覧
②電場と電位とは何かを理解しましょう(「場」とは何か、力学(重力)と電気を対応させて理解する、静電気力、クーロンの法則、静電気力による位置エネルギー(静電エネルギー)、電場と電位をイメージで理解する)
③ガウスの法則はいつどのように使うべきか(電気力線とは何か、電気力線と電場の関係、ガウスの法則の使い方、金属球・金属板・導体棒が作る電場)
④静電誘導と誘電分極(静電遮蔽、雷が発生したとき車の中が安全な理由についても解説しています)
(5)参考
☆物理の解説動画・授業動画一覧(力学・熱力学・波動・電磁気・原子)
☆物理に関する現象や技術(力学、熱力学、波動、電磁気、原子)
