(1)例題
下図は、わずかに異なる二つの振動数f1(実線)とf2(破線)の波(f1>f2)の、ある位置での時間と変位の関係を示している。
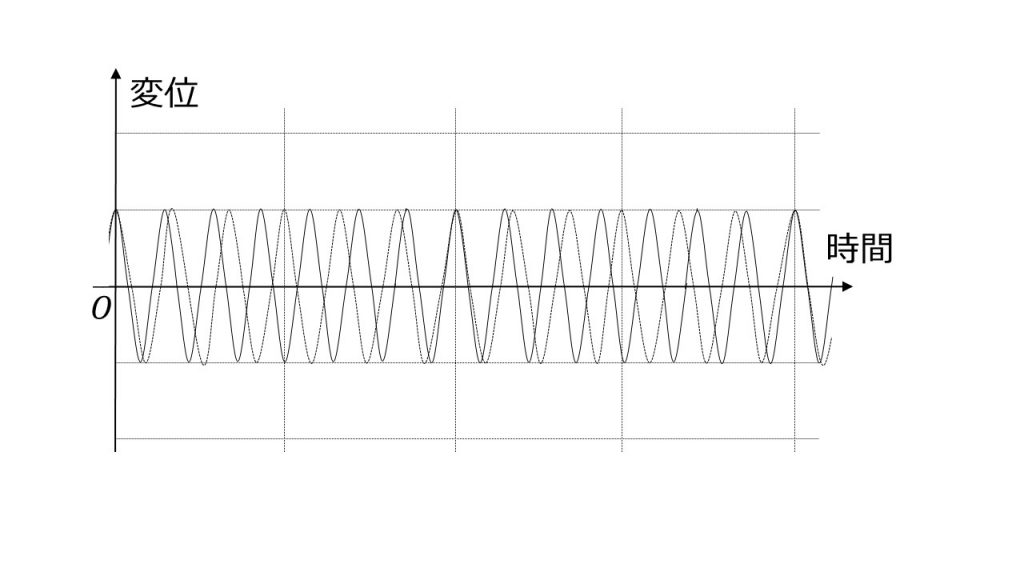
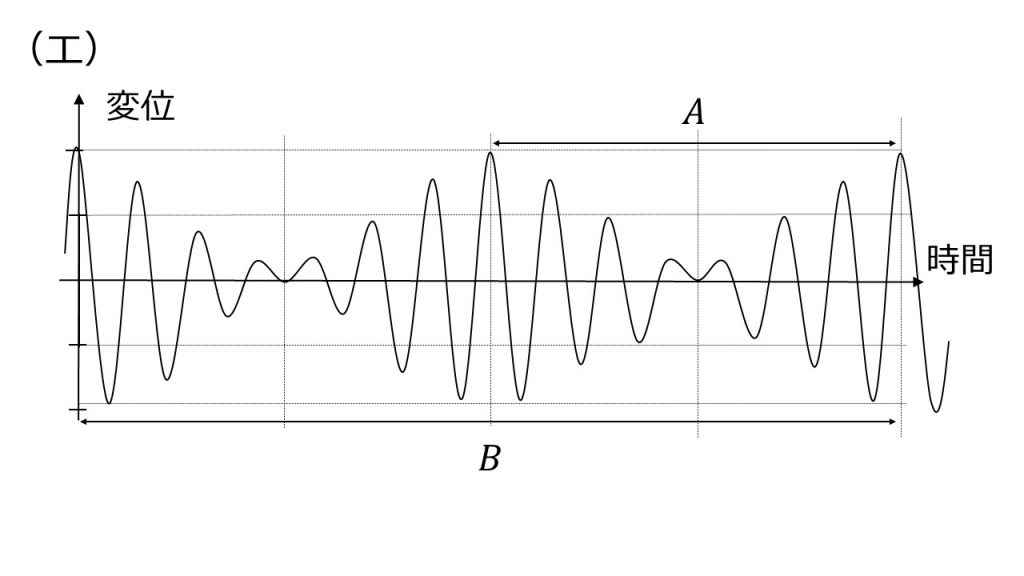
①これら二つの波の合成の、上図と同じ位置での時間と変位の関係を表すグラフは下の(ア)~(エ)のうちどれか。また、うなりの周期はグラフの中に示された時間間隔AとBのどちらか。
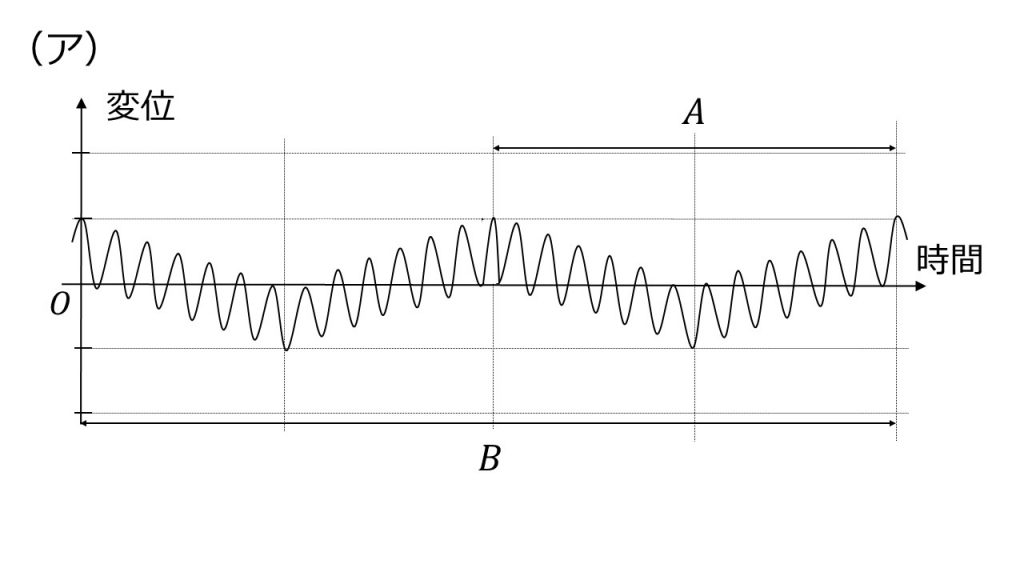
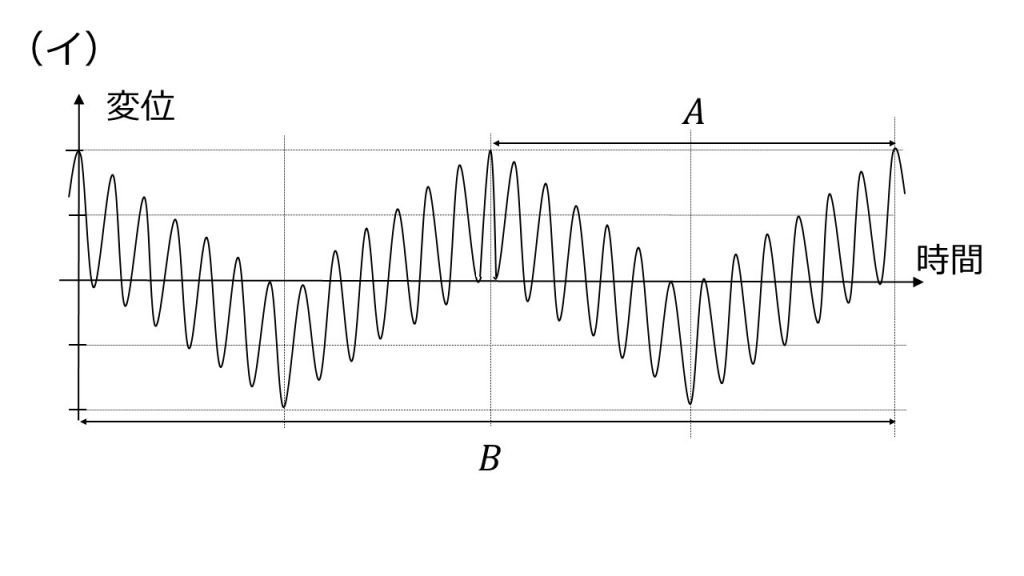
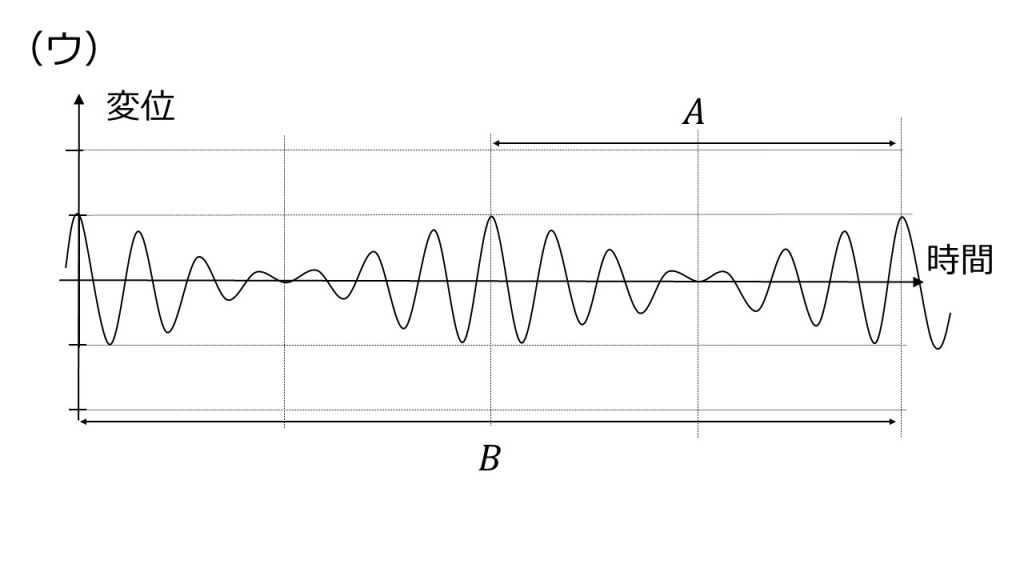
②うなりの周期Tをf1, f2を用いて表せ。
(2018年センター試験本試物理基礎第2問A)
③弦楽器から振動数360Hzの音を発生させ、その近くでおんさを鳴らしたところ、4秒間に8回うなりが聞こえた。弦を張る力を少しだけ強めたところ、弦楽器が発生する音は高くなり、その結果うなりはなくなった。おんさの振動数は何Hzか。
(20187年センター試験本試物理基礎第2問A問2)
(2)答案
①(エ)、A
②f1T−f2T=1
∴ T=1/(f1−f2)
③4秒間に8回うなりが生じているので、1秒間あたりのうなりの回数は2回である。おんさの振動数をf〔Hz〕とすると、弦楽器の振動数が360Hzであるから、うなりの式より
│360-f│=2
∴ f=358〔Hz〕または、362〔Hz〕
弦を張る力を少しだけ強めると、弦楽器が発生する音が高くなったので、振動数は大きくなっている。その結果、うなりがなくなったということは、弦の振動数がおんさの振動数と等しくなったということなので、おんさの振動数は362Hzである。
(3)解法のポイント
①うなりとは、振動数がわずかに異なる二つの波が重なるとき、音の大小が一定の周期で繰り返されて聞こえる現象のことです。
合成波の振幅の最大値は、もとの波の振幅の合計になります。つまり、うなりの周期とは、2つの波の振幅が最大になるときが重なってから、再び重なるまでの時間となります。
②つまり、ある位置に2つの波が届くときに、それらの波の数が一個ずれたとき、2つの波の振幅の最大が重なることになります。ゆえに
f1T−f2T=1
が成り立つのです。
(4)必要な知識
②うなり

