(1)解説授業動画
☆YouTubeチャンネルの登録をよろしくお願いします→大学受験の王道チャンネル
(2)解説授業の原稿
等加速度直線運動の3つの公式
等加速度直線運動の式といえば

この3つなのですが、それぞれの式がなぜこのようになるのか、そして、それぞれの式の関係について解説します。
物理の式を考えるときは、それぞれの文字が何を意味しているのか、そして単位は何なのかを必ず確認しないといけません。
vは速度のことで単位は[m/s]、v0は初速度のことで単位は[m/s]、aは加速度のことで単位は[m/s2]、tは時刻のことで単位は[s]、xは位置のことで単位は[m]となっています。
注意したいのは、vとv0とaとxは負になることもあるということです。速度や初速度がマイナスであるということは、逆方向に進んでいるということであり、加速度がマイナスであるということは減速している、あるいは逆方向に加速しているということであり、位置がマイナスであるということは、正の方向から見て原点より反対側にいるということになります。
1番目の式の成り立ち
それでは、それぞれの文字と単位が確認できたところで、これらの式がなぜこのようになるかを考えてみましょう。
まずは1つ目の式です。そもそもvとは時刻tにおける速度を表しており、「時刻tにおいてある物体の速度がどうなっているかというとv0+atになっている」という意味の式です。
aの意味から式を導く
この式がなぜこのようになっているかを理解するためは、aが表わすものが何かを理解しないといけません。
aとは加速度であり、単位が[m/s2]なのですが、この加速度が意味しているものは何かというと、単位時間当たりの速度の変化を表しています。つまり単位の[m/s2]というのは、「メートル毎秒・毎秒」のことであり、単位時間当たりの速度の変化を表しています。
もう少し簡単にいうと、1秒たつとa[m/s]速度が大きくなるというのが、aが表す意味です。そのため、1秒でa[m/s]速度が大きくなるわけなので、t秒だったらat[m/s]速度が大きくなります。
よって、tにおける速度vは、初速度つまり最初の速度に、t秒間で増加した速度を足したものであるので、v=v0+atとなります。
式の単位を確認しよう
またついでに、この式の単位も確認してみましょう。vの単位は[m/s]です。v0の単位も[m/s]です。そしてaの単位は[m/s2]であり、tの単位は[s]なので、m/s2×sつまりm/sとなります。
このように単位を見てみると、両辺の単位は必ず一致していないといけません。そのため、速度の式を考えるときは、tがt2になったりv0にtがかけられていたりすることはあり得ません。
このように単位を確認するという検算の方法は物理ではとても役に立つので是非やってみてください。
2番目の式の成り立ち
それでは次に2番目の式を考えてみましょう。2番目の式はグラフを使って考えると分かりやすいです。
v-tグラフの読み取り
縦軸をvつまり速度、横軸をtつまり時刻とした、いわゆるv-tグラフを使って考えてみると、xはvのグラフと横軸で囲まれた面積になります。なぜなら、たとえば速度v0でt秒間等速直線運動をした場合、移動距離はv0×tのv0tとなるように、移動距離は速度に時間をかけることで求めることができるからです。
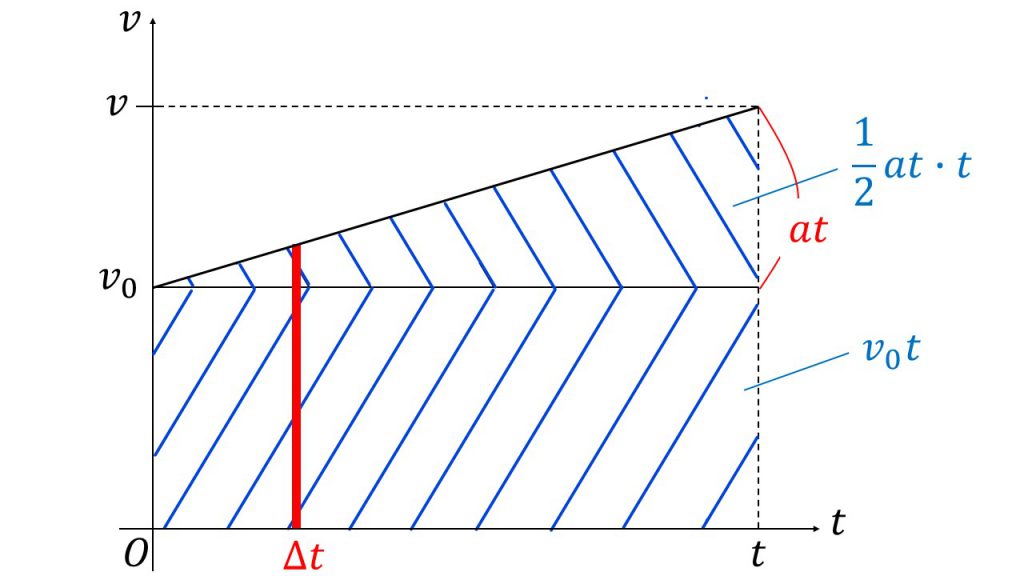
等加速度直線運動の場合は、加速度がかかっているので、速度のグラフは傾きがaの直線となります。しかし、それでも一瞬一瞬で見た場合、その瞬間に進む距離は、
(その瞬間の速度)×(一瞬の時間)
であり、
(ある瞬間に進んだ距離)+(次の瞬間に進んだ距離)+(また次の瞬間に進んだ距離)+……
といったように、0秒の瞬間からt秒の瞬間までをすべて足せば、それが0秒からt秒の間に進んだ距離となります。
ちなみにΔtは「デルタt」と読み、「ほんのわずかな時間変化」と言う意味であるということは知っておきましょう。この瞬間瞬間で見て最後にまとめるという考え方は、積分の考え方なので、詳しくは数学の積分で学習しましょう。
結局のところ、t秒後の位置はv-tグラフの台形の面積であるということなので、この台形の面積を求めてみると、下の長方形の部分は縦がv0で横がtなので、v0tとなり、上の三角形の高さはt秒間で増加する速度なのでatとなり、上の三角形の面積は底辺×高さ÷2で½at2となります。
このように物理でグラフを読み取るときは、傾きと面積が何を意味しているかを考えることが重要になります。今回のv-tグラフであれば、傾きはaつまり加速度を意味しており、面積はxつまり位置を意味しています。
式の単位を確認しよう
また、こちらの式も単位を確認してみましょう。
xの単位は[m]で、v0の単位は[m/s]、そしてtの単位は[s]、aの単位は[m/s2]、t2は[s2]となるので、右辺の単位を計算すると[m]となり、両辺の単位がそろっています。そのため左辺をxとした場合、v0にtがかけられていなかったり、あるいはt2となっていたりすることはあり得ないし、½atになっているということはあり得ません。
3番目の式の成り立ち
それでは3番目の式です。3番目の式は、1番目の式と2番目の式からtを消去して作ります。実際にやってみましょう。
v=v0+atよりt=(v-v0)/a
t=(v-v0)/aをx=v0t+½at2に代入する。
x=v0(v-v0)/a+½a{(v-v0)/a}2
⇔ 2ax=2 v0v-2v02+(v-v0)2
⇔ 2ax=v2-v02
⇔ v2-v02=2ax
まずは1番目の式からt=の形にし、これを2番目の式に代入します。そして、代入した後の式の両辺を2a倍して分母を払い展開して整理したら3番目の式となります。
式の単位を確認しよう
この式も単位を確認してみると、v2は[(m/s)2]であり、v02も[(m/s)2]となります。そして、aは[m/s2]であり、xは[m]となり、これらをかけるとやはり[(m/s)2]となり、両辺の単位がそろっていることを確認できます。
このようにそれぞれの式の導き方を知っておけば、等加速度直線運動の式を使うときに間違えることはなくなるでしょう。
変位・速度・加速度の関係
また、最後に微分と積分を学習している方向けに補足します。
加速度を時間で積分すると速度になり、速度を時間で積分すると変位となります。また、変位を時間で微分すると速度になり、速度を時間で微分すると加速度となります。
そのため、先ほどの等加速度直線運動の式の1番目の式の両辺を時間で積分すると2番目の式となり、2番目の式の両辺を時間で微分すると1番目の式になる、という関係になっています。
v=v0+atの両辺をtで積分すると、速度が変位になり、v0がv0tとなり、atが½at2となります。
また、x=v0t+at2をtで微分すると、変位は速度になり、v0tはv0になり、½at2はatとなります。
ちなみに1番目の式の両辺をさらにtで微分すると、左辺も右辺もaになります。
このように加速度、速度、変位の関係が積分と微分の関係になっていることは物理においてとても重要で、等加速度直線運動だけではなく、円運動などにも当てはまるので数学で微分と積分を習った後は知っておくようにしましょう。
(3)解説授業の内容を復習しよう
(4)平面内の運動の解説一覧
②相対速度の計算で間違えないために(電車の中から見た雨の角度と速度についても解説しています)
③等加速度直線運動の式の成り立ちと関係(v-tグラフの読み取り方、加速度・速度・変位の微分と積分の関係についても解説しています)
④放物運動の考え方(水平投射、斜方投射、斜面での斜方投射、飛行機から物体を落とす、台車から物体を打ち上げる)
(5)参考
☆物理の解説動画・授業動画一覧(力学・熱力学・波動・電磁気・原子)
☆物理に関する現象や技術(力学、熱力学、波動、電磁気、原子)
