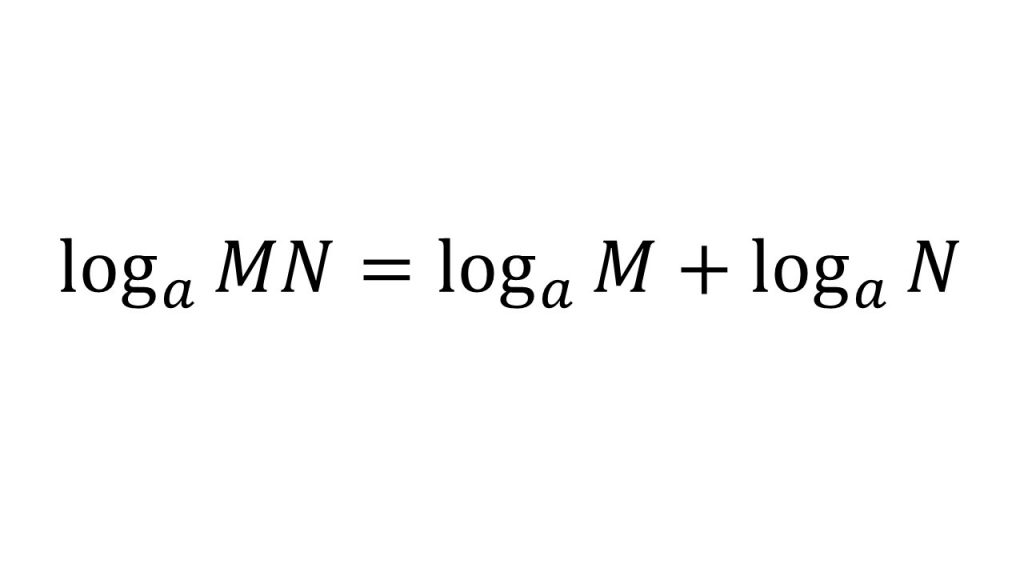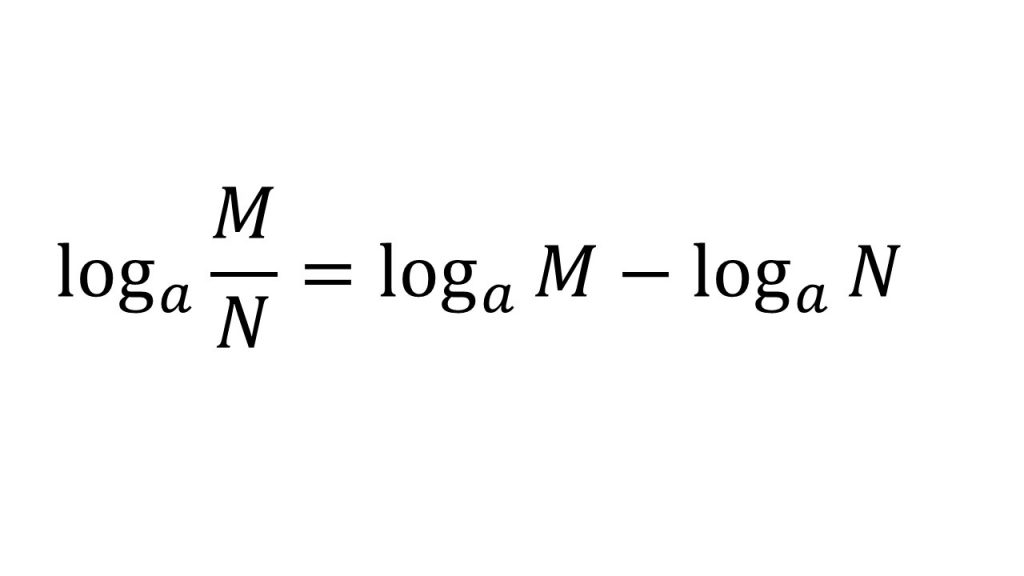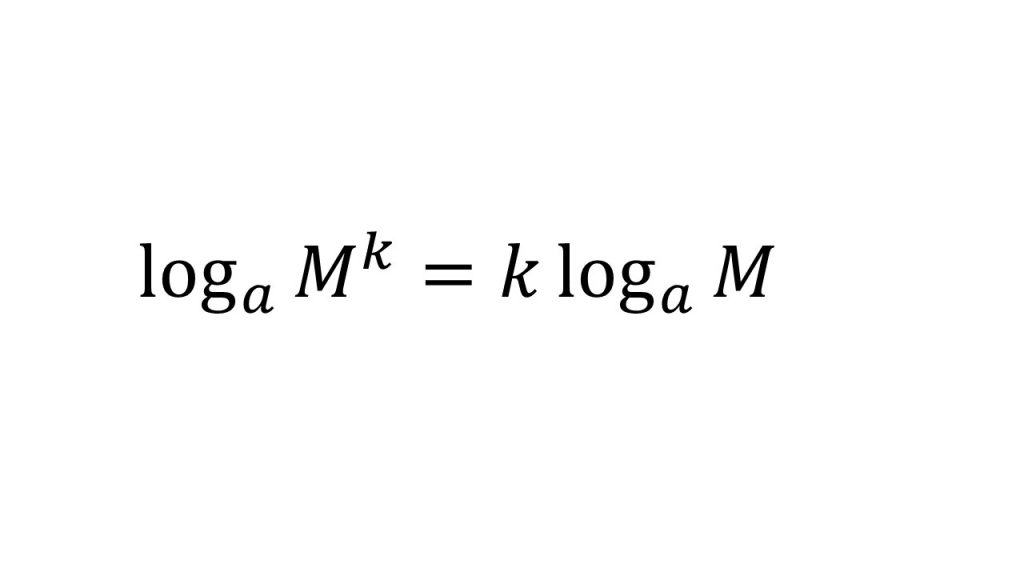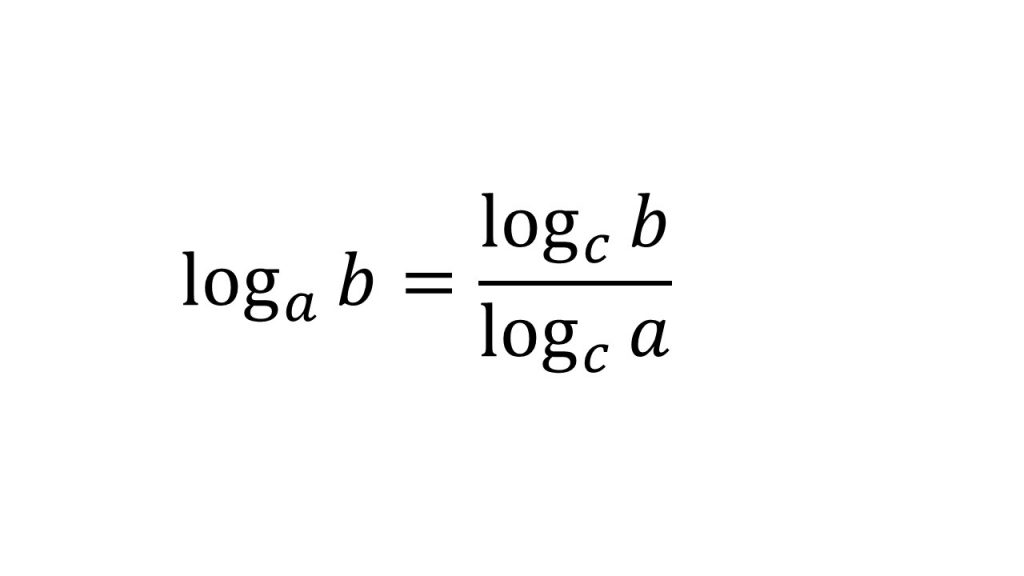(1)例題
①0<a<1として、不等式
2loga(8-x)>loga(x-2)
を満たすxの値の範囲を求めよ。
②1<aとして、不等式
2loga(8-x)>loga(x-2)
を満たすxの値の範囲を求めよ。
(2012年度センター試験本試数学ⅡB第1問〔1〕より)
(2)例題の答案
①真数は正であるから
8-x>0かつx-2>0
よって、2<x<8 ・・・(ア)
また、与式から
loga(8-x)2>loga(x-2)
0<a<1より
(8-x)2<(x-2)
x2-17x+66<0
(x-6)(x-11)<0
6<x<11 ・・・(イ)
(ア)(イ)より、求めるxの範囲は
6<x<8
②真数は正であるから
8-x>0かつx-2>0
よって、2<x<8 ・・・(ア)
また、与式から
loga(8-x)2>loga(x-2)
1<aより
(8-x)2>(x-2)
x2-17x+66<0
(x-6)(x-11)>0
x<6, 11<x ・・・(イ)
(ア)(イ)より、求めるxの範囲は
2<x<6
(3)解法のポイント
1発で①ができたでしょうか? ②を見てから慌てて①を解き直すということがないようにしましょう。
対数不等式の解法の流れは、まず、
真数条件(真数は正)
から不等式をつくります。必ずここから始めてください。
その上で、対数不等式の解法は、以下の2通りがあります。
①底をそろえる→真数を比較
②文字で置き換える
①で底をそろえたり、まとめたりするときは必ず対数の計算公式で計算してください。
また、
底が1より大きければ増加関数となるので、不等号の向きはそのまま
底が1より小さければ減少関数となるので、不等号の向きは逆向きになる
ということに注意しましょう。
②文字で置き換えたときは、必ず範囲を出すことを忘れないようにしましょう。
どちらのやり方でやっても、最後に、真数条件から作った不等式との共通部分を答えにすることを忘れないようにしてください。
(4)必要な知識
①対数の計算公式4つ