(1)例題

(2015年センター試験本試数学ⅡB第4問(2)より)
(2)例題の答案
①
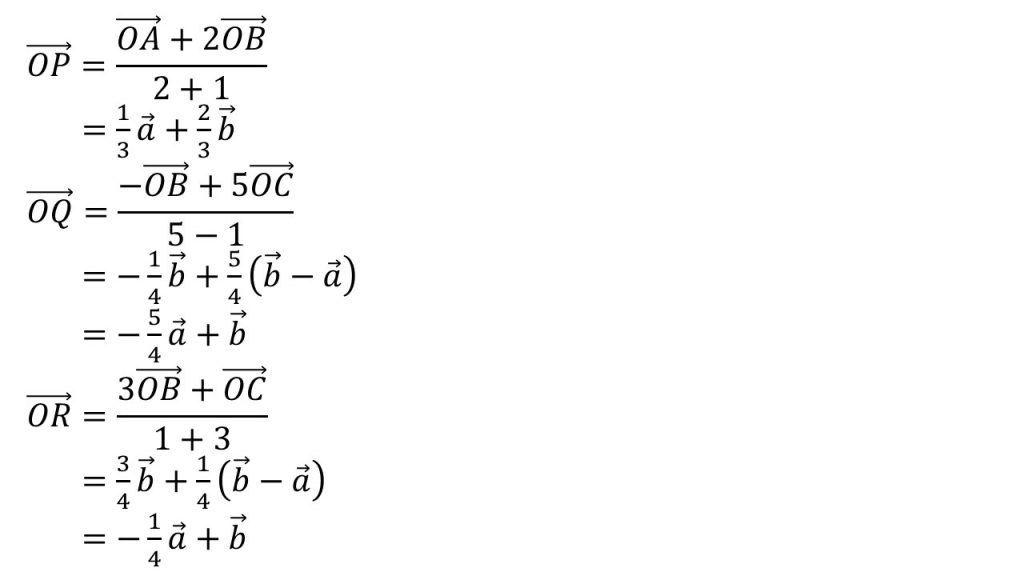

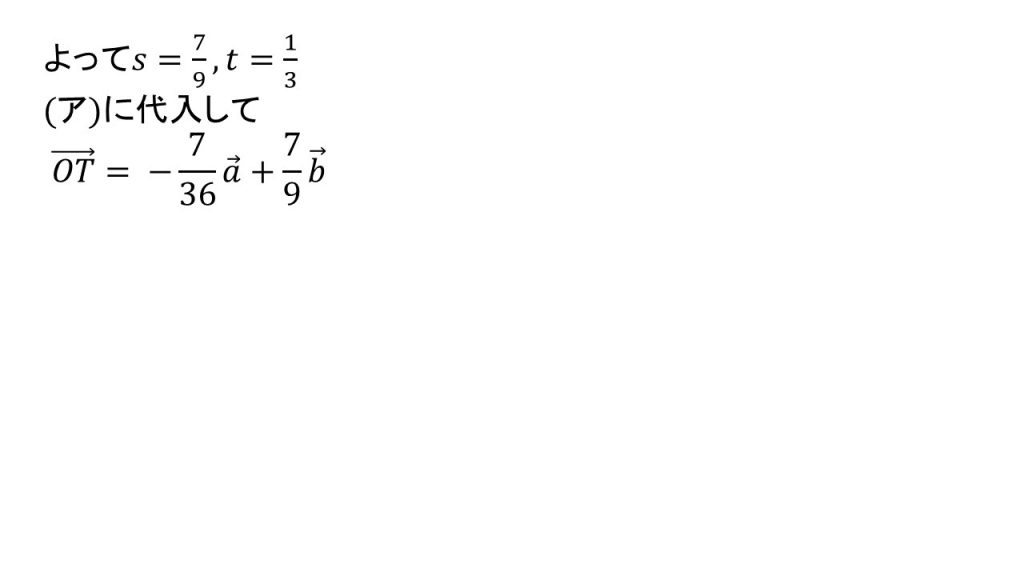
②

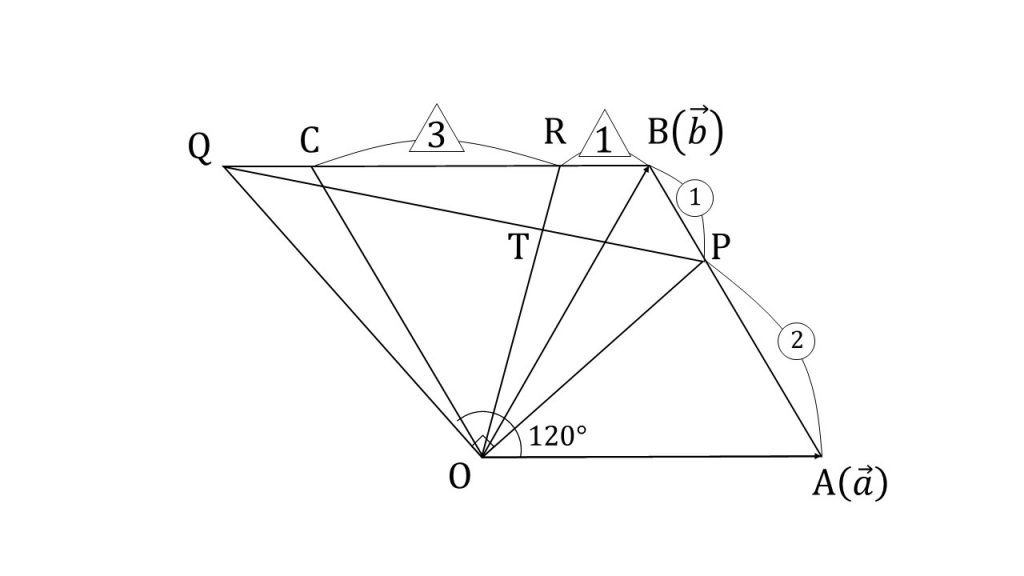
(3)解法のポイント
直線と直線の交点をベクトルで表す問題はベクトルで最も重要な問題です。
ベクトルの問題で「交点」と書かれているときにやるべきことは、
「2通りで表して係数比較」
です。
例えば、「直線ABと直線CDの交点」と問題に書いてあれば、
直線AB上にある条件(ABをt:1-tで内分または外分する点)を式で表し、また、直線CD上にある条件(CDをs:1-sで内分または外分する点)を式で表します。
そして、その2つの式を係数比較(連立)すると、
「直線AB上にあり、かつ直線CD上にある点」
を意味する式ができます。
(4)必要な知識
①内分の位置ベクトル

②外分の位置ベクトル

(5)理解すべきこと
ベクトルの問題で重要な解法を理解しましょう。
動画はこちら↓
