(1)問題
次の二次不等式を解け。
①3x2+20x-7<0
②-x2+2x+5≦0
③x2+2x+1>0
④x2-4x+5>0
⑤4x2-4x+1≦0
⑥-3x2+8x-6>0
(2)答案
①3x2+20x-7<0
⇔ (3x-1)(x+7)<0
⇔ -7<x<⅓

②-x2+2x+5≦0
⇔ x2-2x-5≧0
ここでx2-2x-5=0を解くと
x=1±√6
よって
x≦1-√6, 1+√6≦x
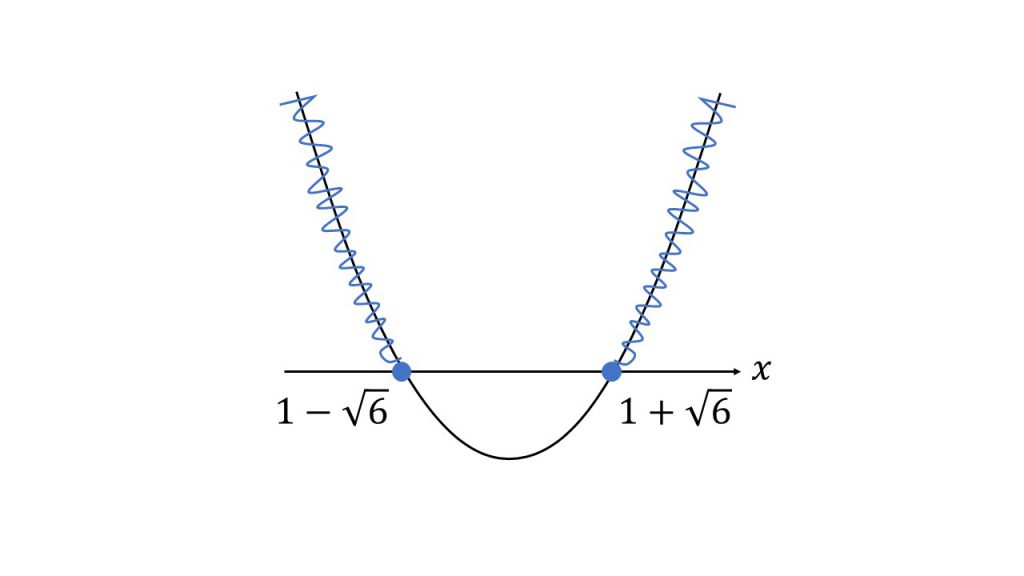
②別解
-x2+2x+5≦0
ここで-x2+2x+5=0を解くと
x=1±√6
よって
x≦1-√6, 1+√6≦x

③x2+2x+1>0
⇔ (x+1)2>0
よって解は、-1以外のすべての実数

④x2-4x+5>0
ここで、x2-4x+5=0とし、この方程式の判別式をDとすると
D=16-20=-4<0
よって解は、すべての実数

⑤4x2-4x+1≦0
⇔ (2x-1)2≦0
よって解は、x=½

⑥-3x2+8x-6>0
⇔ 3x2-8x+6<0
ここで、3x2-8x+6=0とし、この方程式の判別式はDとすると
D=64-4・3・6=-2<0
よって、この二次不等式の解は存在しない。

(3)解法のポイント
二次不等式の解き方は、
①因数分解をする、または(左辺)=0の方程式を解く(解の公式を使って)
②グラフをかく(グラフの正負(x軸よりも上か下か)を読み取る)
この流れが基本です。
また、不等号に=が含まれているかに注意してください。
二次不等式の解が、「解なし」「全ての実数」「〇を除くすべての実数」「x=〇」といったものになる場合もあります。
(4)理解すべきこと
二次不等式の解法の流れを理解しましょう→二次不等式の解法(解が特殊になる二次不等式の解説もしています)
☆動画はこちら↓
