(1)例題
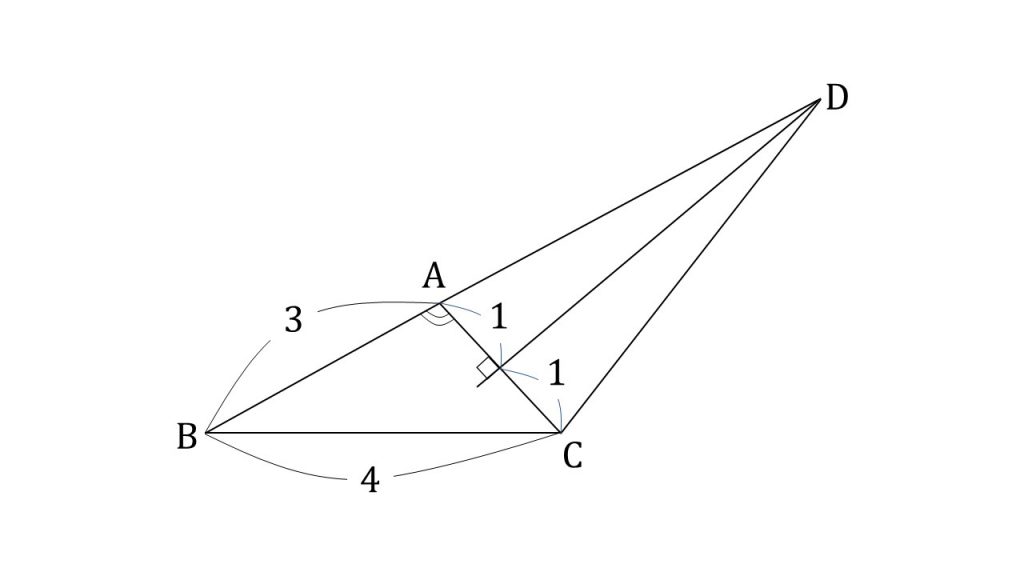
△ABCにおいて、AB=3, BC=4, AC=2とする。
①∠BACは鋭角か鈍角か。
②sin∠BACを求めよ。
線分ACの垂直二等分線と直線ABの交点をDとする。
③ADを求めよ。
④△DBCの面積を求めよ。
(2019年センター試験本試数学ⅠA第2問〔1〕)
(2)例題の答案
①

②

③

④
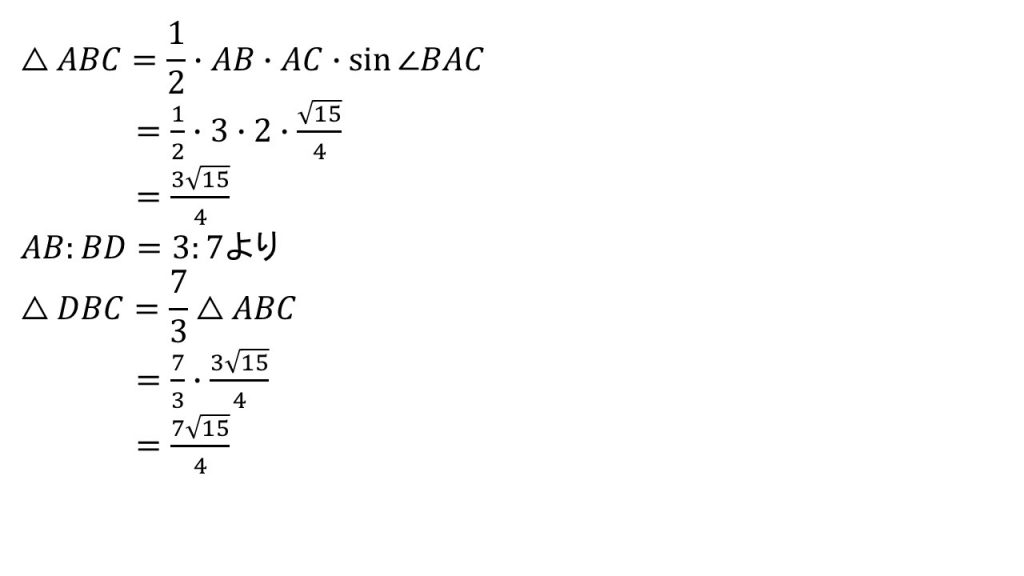
※それまでに求めたものを最大限に使った答案である。その他に、sin∠ABCを求めて△DBCを求める答案や、sin∠CADを求めて△DACを求める答案などが考えられる。
(3)解法のポイント
①鋭角か鈍角かの判別をするときは、コサインを利用します。
②三角形の内角であれば、0°より大きく180°より小さくなるので、サインは正となります(コサインとタンジェントは負の場合もある)
③直角三角形ができたときは、正弦定理・余弦定理を使うよりも
底辺=斜辺×cosθ
高さ=斜辺×sinθ
高さ=底辺×tanθ
を利用しましょう。その方が早くてラクです。
(4)必要な知識
①直角三角形と三角比

②三角比の相互関係の3つの式

③180°-θ、90°-θ、90°+θの三角比
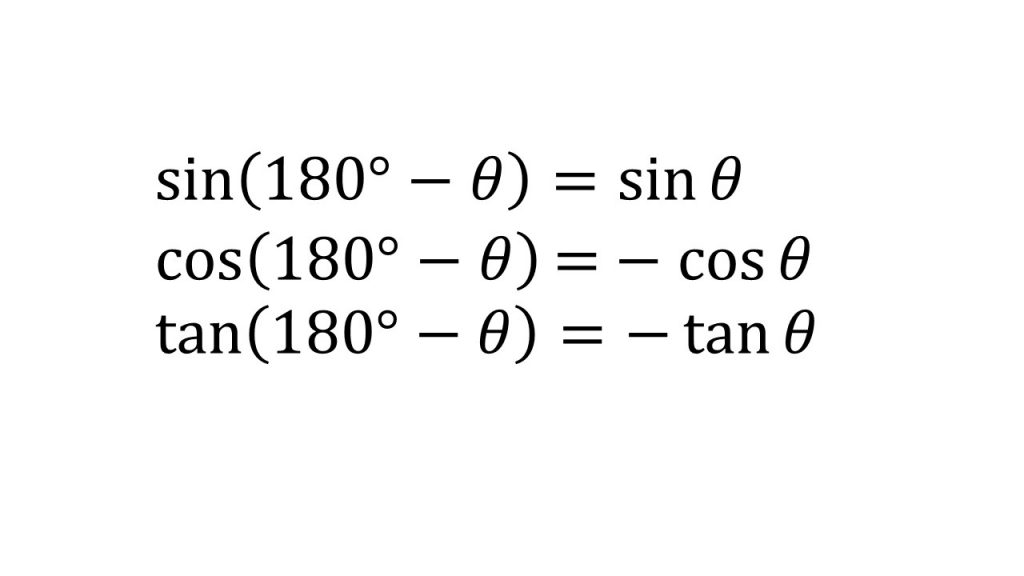
④余弦定理

⑤三角形の面積の公式2つ

