(1)例題
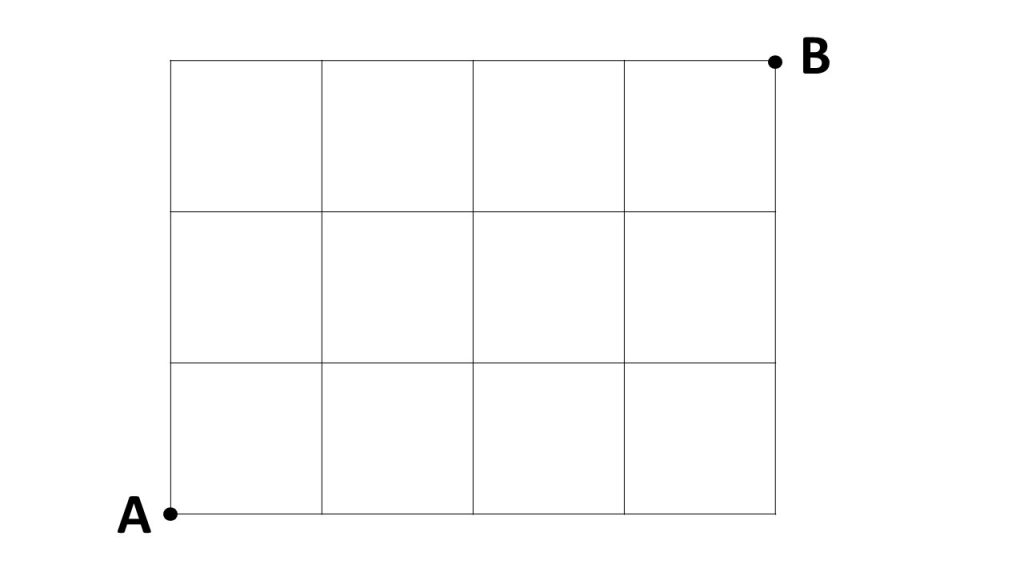
①下の図のAからBまで最短で行く方法は何通りあるか。
(2)例題の答案
①↑↑↑→→→→の順列を考えればよいので
7!÷3!÷4!=35 通り
(3)解法のポイント
碁盤の目状の道路をある地点からある地点まで最短で行く行き方を考える問題の考え方は、
上に進むことを、↑
右に進むことを、→
として考え、この↑と→の同じものを含む順列と考えます。
また、Cを使って考えることもでき、その場合は、
「移動回数のうち上に進む(あるいは右に進む)行為を何回目に行うか」
と考えます。
(4)必要な知識
①同じものを含む順列

(5)理解すべきこと
同じものを含む順列の原理を理解しましょう→同じものを含む順列の原理(なぜ同じものの階乗で割るのか、最短経路)
☆動画はこちら↓
