(1)例題
①年利15%で100万円借金をし、5年後に全額返した場合、返済する金額はいくらか。ただし、(1.15)5=2.011とする。
②年利5%、1年ごとの複利で、毎年度初めに12万円ずつ積み立てると、10年度末には元利合計はいくらになるか。ただし、(1.05)10=1.63とする。
(2)例題の答案
①
1000000×(1.15)×(1.15)×(1.15)×(1.15)×(1.15)=1000000×(1.15)5=1000000×2.011=2011000円
②
120000×(1.05)10+120000×(1.05)9+120000×(1.05)8+……+120000×(1.05)2+120000×(1.05)
=120000×(1.05){(1.05)10−1}/(1.05−1)
=120000×(1.05)×0.63÷0.05
=120000×21×0.63
=1587600円
※初項120000×(1.05)、公比1.05、項数10の等比数列の和
(3)解法のポイント
そもそも複利とは何かを理解しないといけません。
例えば、100万円を年利15%で借金したとしましょう。すると1年後に借金は(元利合計で)100万×1.15=115万円となります。そして、さらに1年後どうなるかといえば、130万円ではなく、
115万×1.15=132万2500円となります。
つまり、利息というのは毎年決まった額が加算されるのではなく、そのときの元利合計(元金+利息)に応じて加算されるのです。上の例では、毎年15万円ずつ借金が増えるのではなく、毎年1.15倍されていくわけです。これが借金が雪だるま式に増えていく理由です(例題にもあるように約5年で2倍になります。ちなみに年利15%というのは、いわゆる消費者金融の一般的な利率です)
また、積立預金とは毎年決まった額を入金(積立)する預金方法のことです。
こちらも例で考えてみると、毎年100万円、年利5%で5年積立預金をしたとしましょう。すると、
1年目に預けた100万円は5年目の末に、100万×(1.05)⁵円
2年目に預けた100万円は5年目の末に、100万×(1.05)⁴円
……
5年目に預けた100万円は5年目の末に、100万×1.05円
となり、これらを合計したものが受け取ることのできるお金となります。よって合計金額は、
100万×(1.05)⁵+100万×(1.05)⁴+……+100万×1.05
となり、これは等比数列の和となっているのです(初項100万×1.05、公比1.05、項数5の等比数列の和)
(4)必要な知識
①等比数列

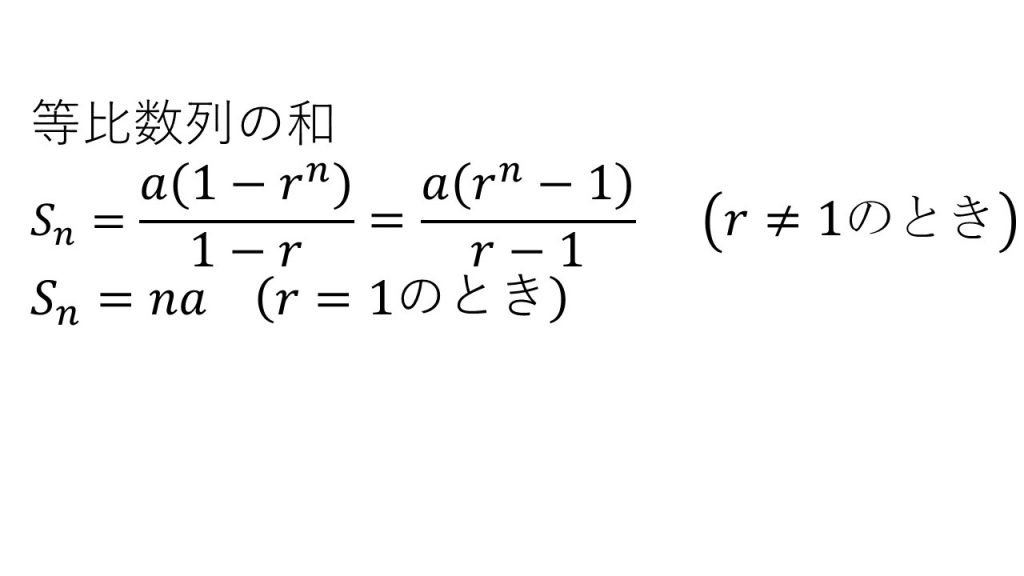
(5)理解すべきこと
そもそも複利とは何かから理解しましょう→複利計算の解説(そもそも複利とは何か、積み立て預金の計算について解説しています)
☆動画はこちら↓
