(1)例題
①右向きに2m/sの速さで移動する物体Aと、右向きに3m/sの速さで移動する物体Bがある。物体Aから見た物体Bの相対速度を求めよ。
②左向きに2m/sの速さで移動する物体Aと、右向きに3m/sの速さで移動する物体Bがある。物体Aから見た物体Bの相対速度を求めよ。また、物体Bから見た物体Aの相対速度も求めよ。
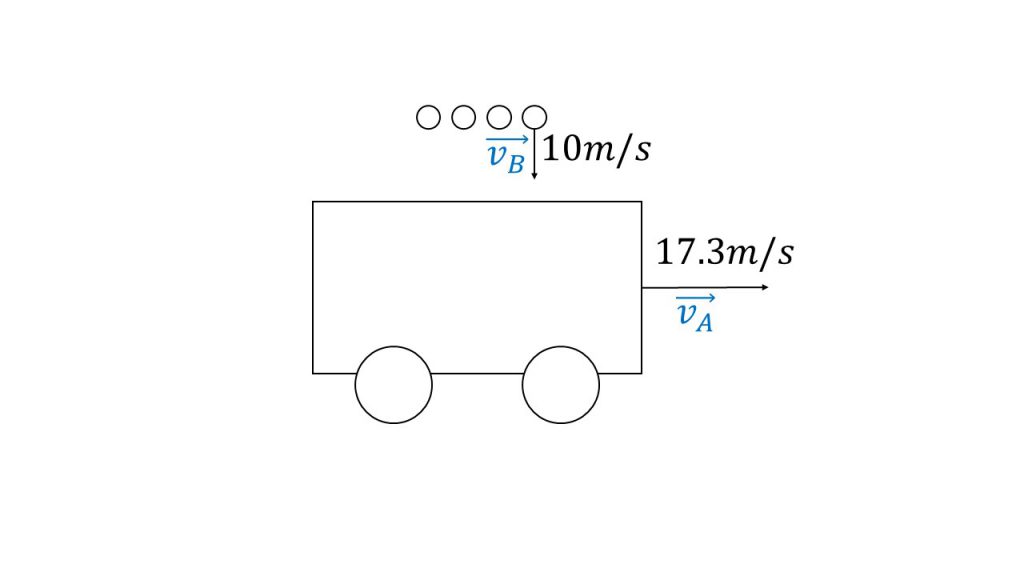
③東に17.3m/sの速さで走る電車の中から、10m/sの速さで鉛直下向きに落ちる雨を観測したとき、雨の角度と速さはどのように見えるか。
(2)例題の答案
①物体Aから見た物体Bの相対速度をvABとすると
vAB=3-2=1m/s
よって、右向きに1m/s
②物体Aから見た物体Bの相対速度をvABとすると
vAB=3-(-2)=5m/s
よって、右向きに5m/s
物体Bから見た物体Aの相対速度をvBAとすると
vBA=-2-3=-5m/s
よって、左向きに5m/s
③電車の速さをvB、雨の速さをvAとする。電車から見る雨の速さvABは
vAB=vBーvA
である。
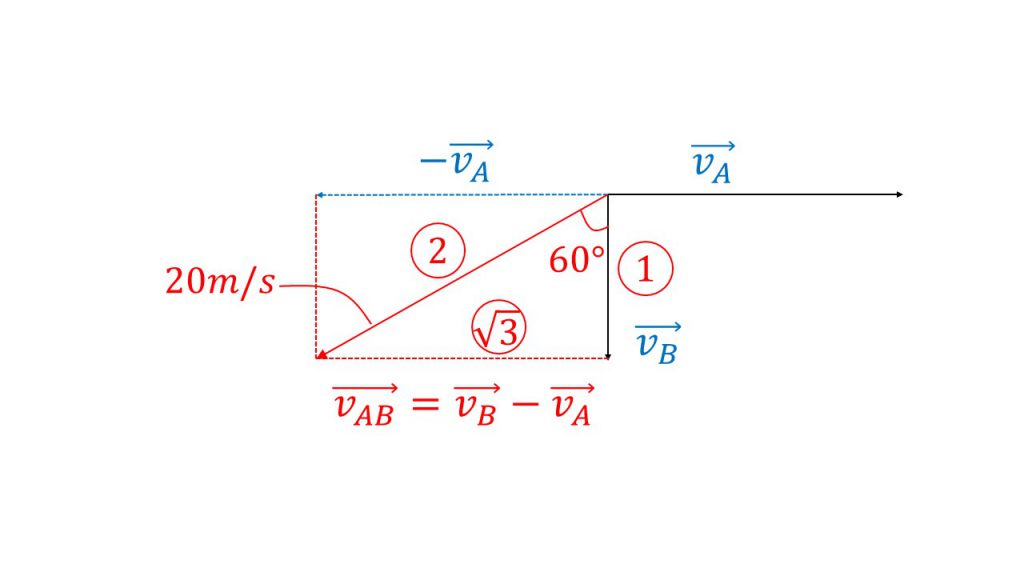
vA:vB:vAB=√3:1:2より
鉛直下向きから西に60°の角度で、速さは20m/s
(3)解法のポイント
相対速度を考えるときは、どちらが観測者で、どちらが観測される対象なのかを確認しましょう。
(観測される対象の速度)-(観測者の速度)
を計算することで、相対速度は求められます。これはベクトル(平面または空間内の運動)であろうと同様です。
(4)必要な知識
①相対速度

(5)理解すべきこと
相対速度の計算の仕方を理解しましょう→相対速度の計算で間違えないために(電車の中から見た雨の角度と速度についても解説しています)
☆動画はこちら↓
(6)参考
☆平面内の運動の勉強法はこちら→平面内の運動
☆力学の勉強法はこちら→力学の勉強法
