(1)例題
図aのように、十分大きくなめらかな円錐面が、中心軸を鉛直に、頂点Oを下にして置かれている。大きさの無視できる質量mの小物体が円錐面上を運動する。頂点Oにおいて円錐面と中心軸のなす角度をθとし、重力加速度の大きさをgとする。
図a
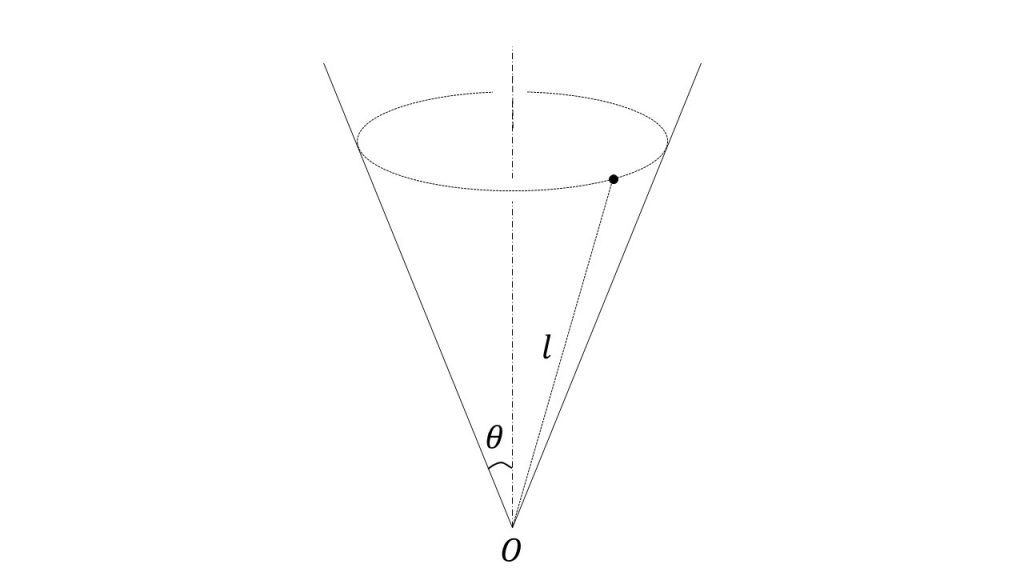
図bのように、頂点Oから距離ℓ1の点Aで、大きさv1の初速度を与えたところ、小物体は円錐面に沿って運動し、頂点Oから距離ℓ2の点Bを通過した。点Bにおける小物体の速さを表せ。
図b

(2017年センター試験本試物理第4問A問3)
(2)答案

(3)解法のポイント
力学的エネルギー保存の法則は、保存力(重力や弾性力など)以外の外力によって仕事をされていないときに使えます。
今回は、保存力以外の外力は垂直抗力ですが、垂直抗力は小物体の移動方向と垂直な方向に働く力なので、仕事をしていません(W=F・0=0)
よって、力学的エネルギー保存の法則が使えます。
(4)必要な知識
①力学的エネルギー保存の法則

(5)理解すべきこと
保存力とは何かを理解し、重力による位置エネルギーとは何か理解しましょう→位置エネルギーとは何かを説明できるようになりましょう(重力・弾性力・万有引力・静電気力による位置エネルギー、保存力とは何か、仕事と運動エネルギーの関係についても解説しています)
☆動画はこちら↓
(5)参考
☆仕事とエネルギーの勉強法はこちら→仕事と力学的エネルギー
☆力学の勉強法はこちら→力学の勉強法
