(1)例題
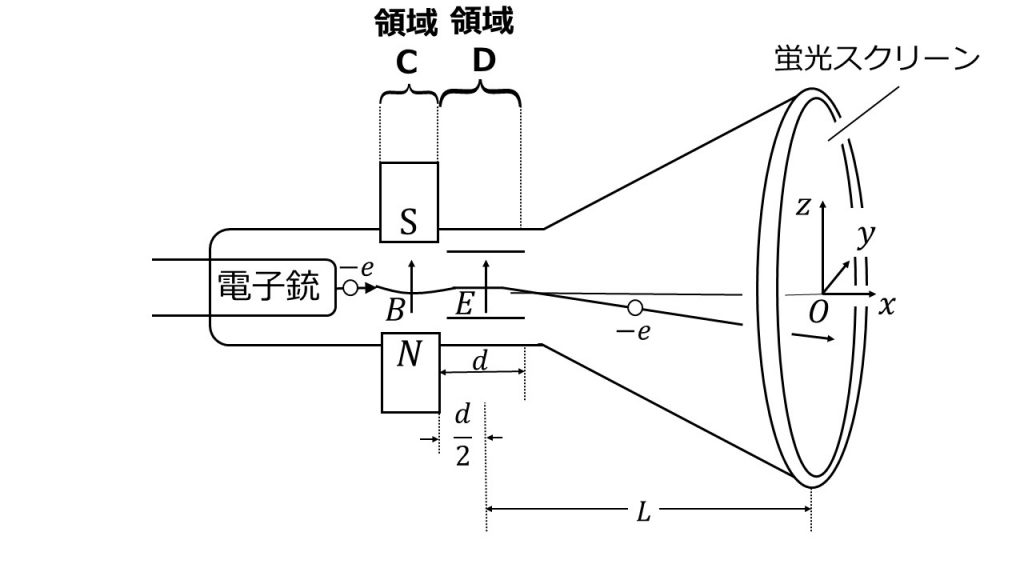
図1のように、領域Cに一様な磁場、領域Dには一様な電場が加わる真空管がある。領域Dのx軸方向の長さはdである。電子銃からx軸に沿って速さv0で発射された電子は、となりあった領域Cと領域Dを通って、領域Dの中心から+x軸方向に距離Lだけ離れた蛍光スクリーンに到達する。スクリーンはx軸に垂直に置かれており、領域Cと領域Dに磁場、電場がないときには、電子はスクリーン上の原点Oに到達する。以下では、領域Cに磁束密度Bの磁場を+z軸方向に加え、領域Dには電場Eを+z軸方向に加える。このとき電子は領域Cと領域Dを、図2のように通過してスクリーンに到着した。その到着位置を(y, z)と表す。電子の電荷は-e、質量はmとし、重力の影響は無視する。各問いでは{ }内に示されている記号のうち、必要なものを用いて解答せよ。
領域C内では、電子は磁場から(①){v0, e, m, B}の大きさの向心力を受け、図2のように半径(②) {v0, e, m, B}の円弧をえがいて運動する。電子が領域Cから出るときの運動方向とx軸がなす角をθ(>0)とする。領域Cから出るまでに電子が+y軸方向に移動した量ycは、(③) {v0, θ, e, m, B}である。電子が領域Dに入ってから、スクリーンに到着するまでに要する時間は(④) {v0, θ, e, m, E, d, L}である。電子のスクリーン上での到達位置は、y=(⑤){yc, v0, θ, e, m, E, d, L}、z=(⑥){v0, θ, e, m, E, d, L}となる。

(岡山大学入試問題より)
(2)例題の答案
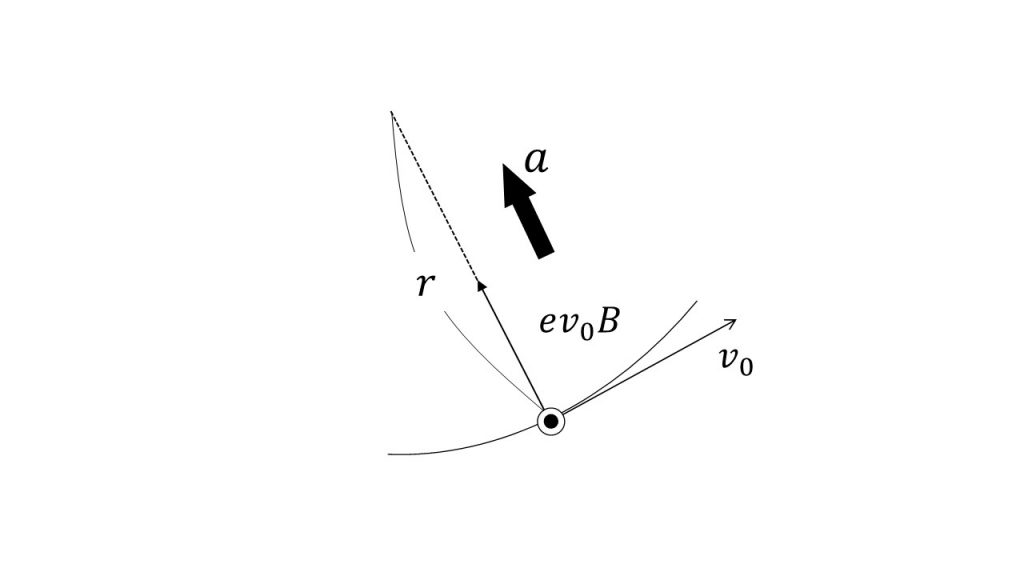
①磁場中で電子はローレンツ力を受けるので、
f=ev0B
の大きさの力を受ける。
②

③

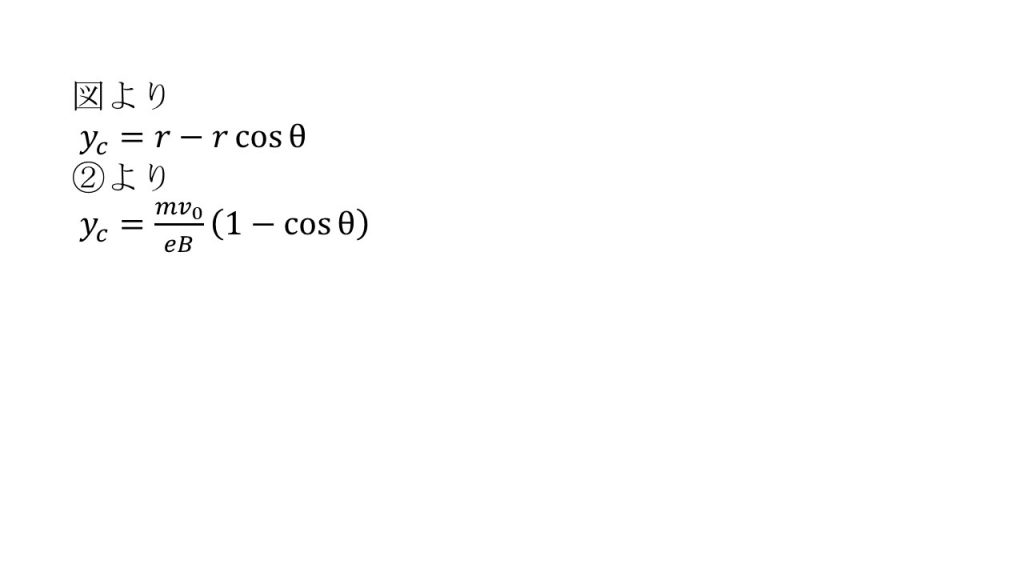
④

⑤

⑥




(3)解法のポイント
荷電粒子の運動の問題は、
①磁場中 → f=ev0Bの大きさの力をフレミングの左手の法則の向きに受ける(正電荷が移動する方向を電流の向きとする)
②電場中 → f=qEの大きさの力を、正電荷なら電場と同じ方向に、負電荷なら電場と逆方向に受ける
この2つがまず重要です。
力の大きさと向きが分かったら、あとは力学の問題として考えましょう(等速直線運動、等加速度直線運動、円運動)
また、図をかくことも重要です。
3次元(x,y,z)のときは、平面で切り取って図をかくようにしましょう。
(4)必要な知識
①ローレンツ力

②電荷が電場から受ける力

③等速直線運動

④等加速度直線運動

⑤運動方程式

⑥向心加速度

⑦向心力

(5)理解すべきこと
①電場と電位とは何かを理解しましょう(「場」とは何か、力学(重力)と電気を対応させて理解する、静電気力、クーロンの法則、静電気力による位置エネルギー(静電エネルギー)、電場と電位をイメージで理解する)
②等速円運動の問題の2つの解法について理解しましょう→等速円運動の2つの解法(向心力と遠心力についても解説しています)
