(1)例題
下の図は、ある町の街路樹の一部である。
ある人が、交差点Aから出発し、次の規則に従って、交差点から隣りの交差点への移動を繰り返す。
ア.街路上のみを移動する。
イ.出発前にサイコロを投げ、出た目に応じて上図の1~6の矢印の方向の隣りの交差点に移動する。
ウ.交差点に達したら、再びサイコロを投げ、出た目に応じて図の1~6の矢印の方向の隣りの交差点に移動する。(一度通った道を引き返すこともできる。)
エ.交差点に達するたびに、ウと同じことを繰り返す。
①交差点Aを出発し、4回移動して交差点Bにいる確率を求めよ。
②交差点Aを出発し、3回移動して交差点Cにいる確率を求めよ。
③交差点Aを出発し、3回の移動が終わった時点で交差点Cにいて、次に3回移動して交差点Dにいる確率を求めよ。
④交差点Aを出発し、6回移動して交差点Dにいる確率を求めよ。
(2014年センター試験本試数学ⅠA第4問改)
(2)例題の答案
①

②

③

④


①別解

②別解

③別解

④別解

(3)解法のポイント
移動する点の問題は、確率を求めるときは反復試行の確率で、場合の数を求めるときは、同じものを含む順列で考えます。
(4)必要な知識
①反復試行の確率
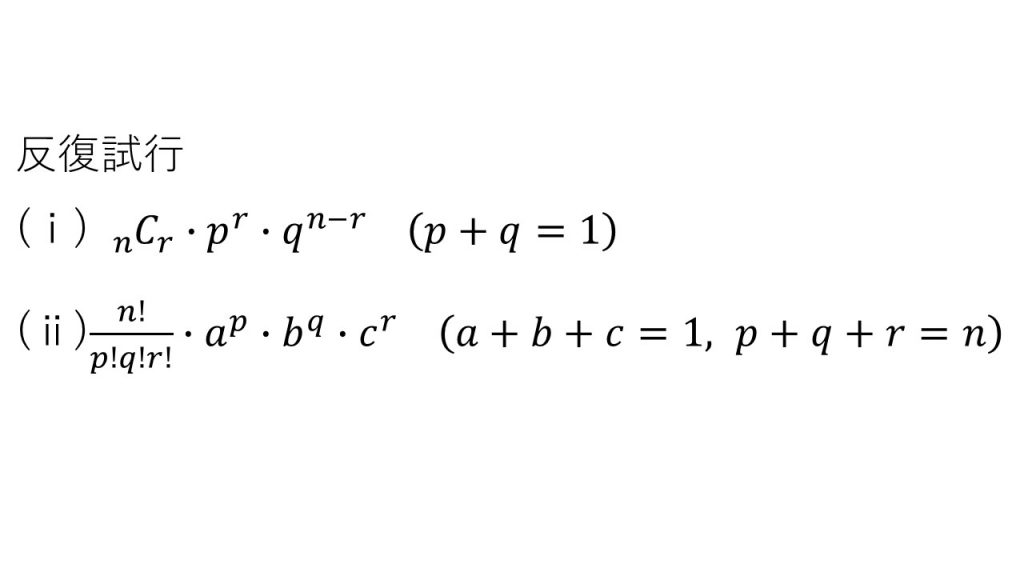
②同じものを含む順列

③確率の定義

反復試行の確率の公式の意味を理解しましょう→反復試行の確率の式の意味(なぜnCrをつけるのか、3つ以上の反復試行の確率の求め方についても解説しています)
