(1)例題

(センター試験数学ⅠA第1問〔2〕(2)より)
(2)例題の答案
①

②

(3)解法のポイント
必要条件や十分条件を調べるときは、p⇒qとq⇒pを分けて、順番に真偽を考えるようにしましょう。
偽であることをいうためには、反例を示さないといけないことにも注意しましょう。反例を探すときは、0など特殊な値に注目すると見つけやすくなります。
また、有理数と無理数の特徴として、
①有理数どうしを四則演算(+、-、×、÷)をしても有理数である
②有理数と無理数を足したり、引いたりしたら無理数である(掛け算や割り算は0にすることができる)
この2つを知っておきましょう。
(4)必要な知識
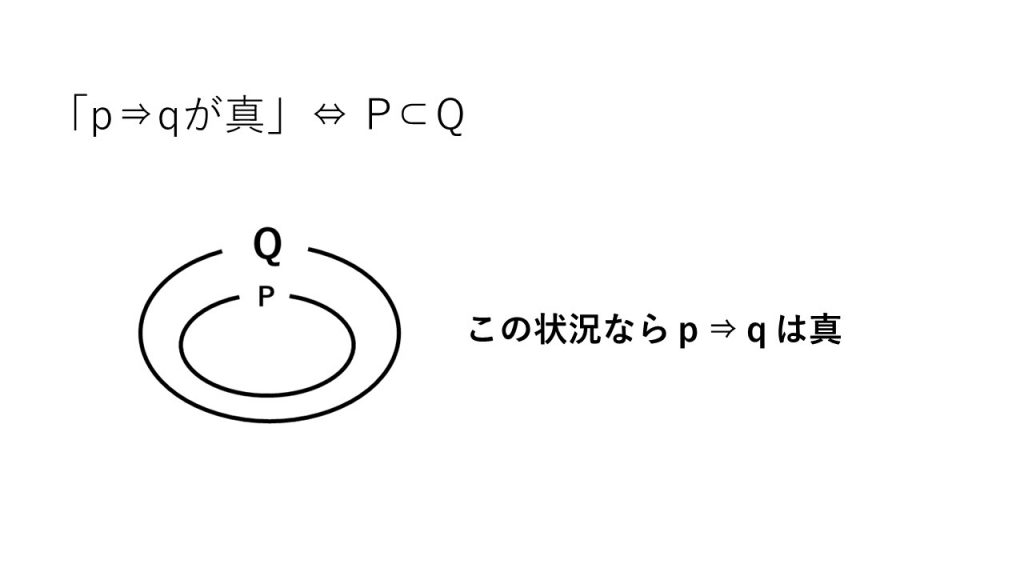
①「p⇒qが真」⇔ P⊂Q
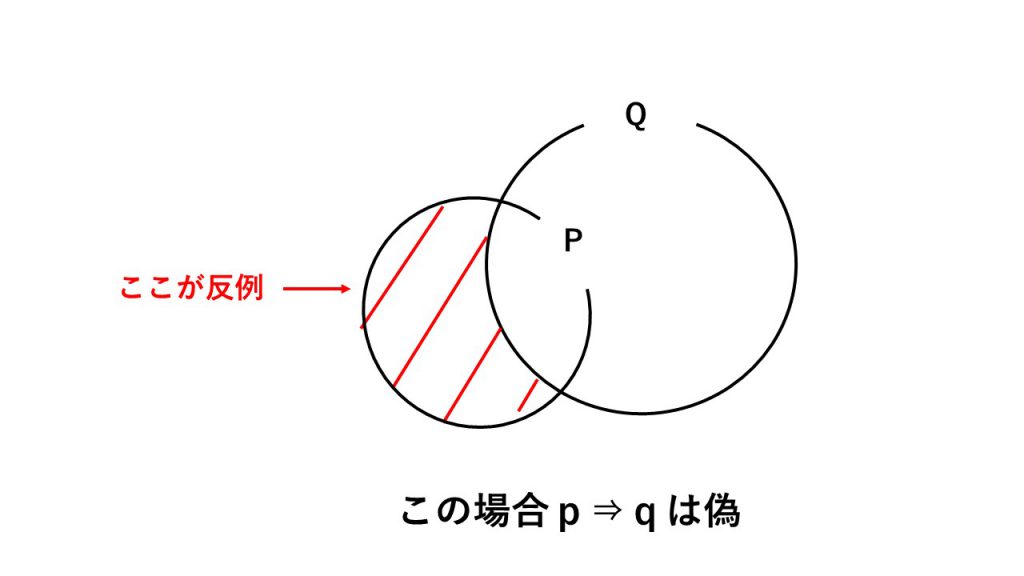
②反例の見つけ方
→pならばqの反例:pを満たし、かつ、qを満たさないもの
③pはqであるための○○条件
・p⇒qが真:十分条件
・q⇒pが真:必要条件
・p⇒qが真、かつ、q⇒pが真:必要条件(同値)
④有理数:整数p、qを使ってq/pと表すことができる数
※循環小数は有理数
※有理数どうしで四則演算(+、-、×、÷)をしても有理数である。
⑤無理数:有理数ではない実数
