(1)解説授業動画
☆YouTubeチャンネルの登録をよろしくお願いします→大学受験の王道チャンネル
(2)解説授業の原稿
放物運動は水平方向と鉛直方向に運動を分解する
放物運動とは水平投射と斜方投射のことを言います。
これらの問題を考えるときは、必ず水平方向と鉛直方向に運動を分解して考えます。
水平投射と斜方投射はどちらも水平方向だけ考えると等速直線運動となっており、鉛直方向だけ考えると加速度がgまたは-gの等加速度直線運動となります。鉛直下向きを正とした場合の加速度はgとなり、鉛直上向きを正とした場合の加速度はマイナスgとなります。
水平投射を分解して考える
高台から物体を水平に投射する
例えば、下図のように高台から物体をV0で水平投射した場合、物体は放物運動をします。
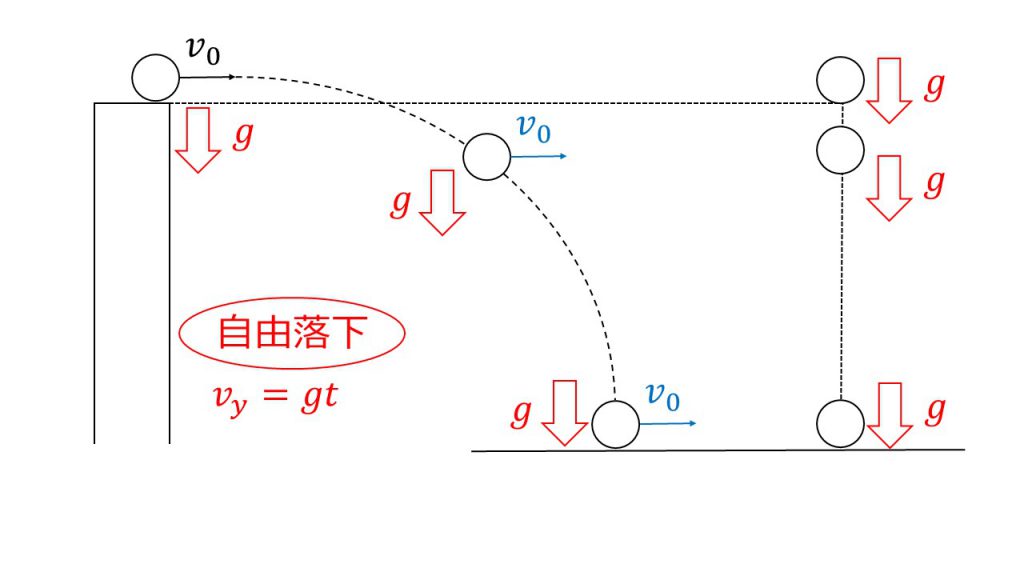
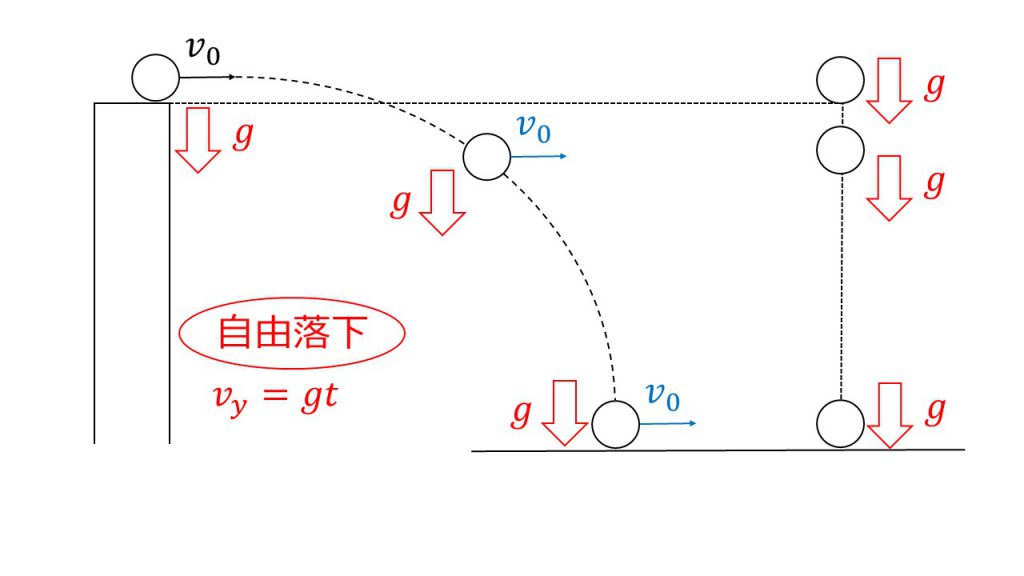
このような水平投射の場合は水平方向は等速直線運動なので、たとえどこにいたとしても、水平方向の速度はすべて初速度と同じV0となります。
そして、鉛直方向は等加速度直線運動をするので、どこにいても同じgの加速度を受けることになります。そのため、この物体は鉛直方向だけを考えると自由落下をしているのと同じなので、下向きを正とすれば、鉛直成分の速度は等加速度直線運動の式を考えてgtとなります。
飛行機から物体を落とす
また、例えば速度vで水平方向に等速直線運動をしている飛行機から物体を落としたとき、その物体は水平投射されたように放物運動をするのですが、物体は常に飛行機の真下に来ます。
なぜなら水平方向だけを考えると飛行機も物体も共に速度vの等速直線運動しているからです。

水平投射と自由落下の関係
さらに、同じ高さから、水平投射をした場合と、そのまま下に自由落下をさせた場合の、地面に着地するまでの時間は等しくなります。
なぜなら、ともに鉛直方向だけを見れば加速度gの自由落下をしているからです。
斜方投射を分解して考える。
基本的な斜方投射
次に、下図のような斜方投射も考えてみます。例えば水平面からθの角度をつけて物体を投げたとき、物体は放物線を描いて運動をします。
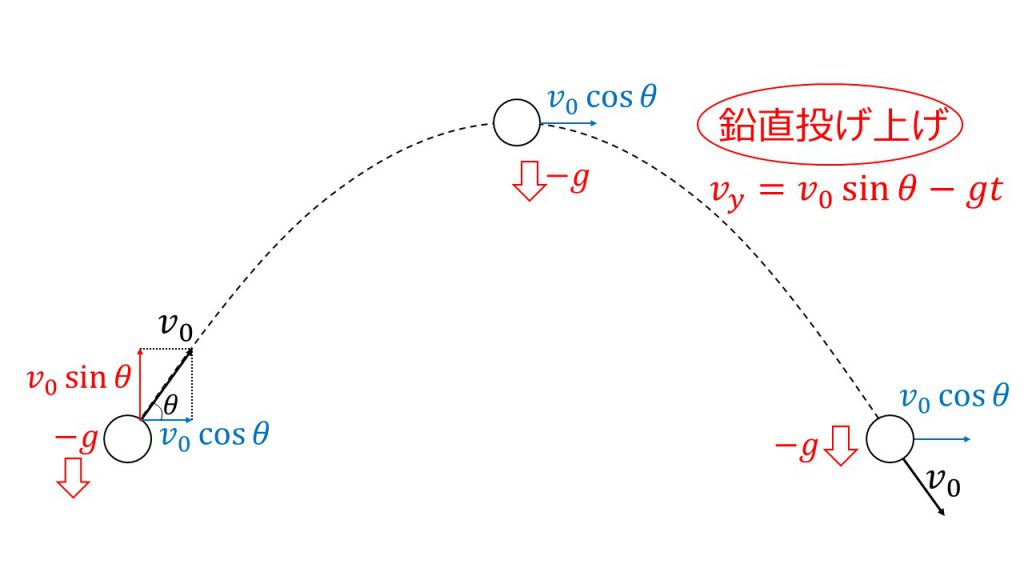
このような運動の場合、水平方向は等速直線運動をしているので、たとえどこに物体があったとしても水平方向の速度はV0cosθとなります。
また、鉛直方向は鉛直上向きを正とした場合、どこに物体があっても常に-gの加速度を受けるので、鉛直方向だけ見れば鉛直投げ上げをしているのと同じ状況となり、鉛直成分の速度はV0sinθ-gtとなります。
さらに、投げた高さと同じ高さに落ちてくるときは、その速度の大きさは投げたときと同じV0となります。これは実際に計算してみてもそうなりますし、力学的エネルギーの保存則を考えてみてもこうなることがわかります。
台車から球を打ち出す
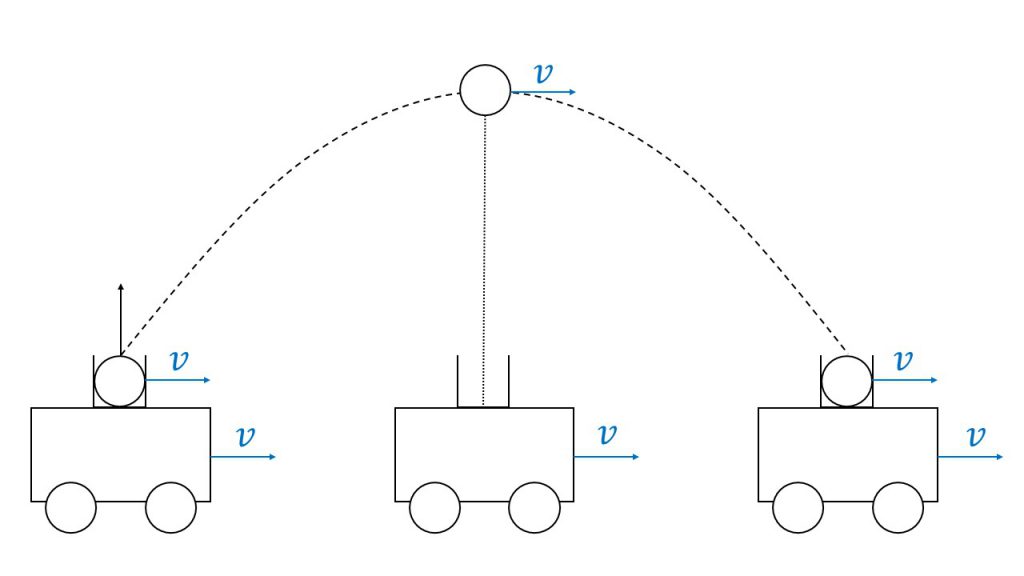
例えば、速度vで等速直線運動をしている台車から球を打ち出したとき、その球は斜方投射と同じように放物運動となるのですが、球は常に台車の真上に来ることになり、最終的には台車の元の位置に落下することになります。
それはなぜかというと、台車も玉も常に水平方向は同じ大きさのvの速度で等速直線運動をしているので、必ずこのような位置関係となるのです。
斜面での斜方投射
それでは最後に斜面で斜方投射をしてみたとき、どうなるかを考えてみましょう。
斜面の場合は、地面に対して水平方向と鉛直方向に分解するのではなく、斜面に対して水平方向と垂直な方向に分解するようにしましょう。軸を斜面に対して水平と垂直で考える場合は、重力加速度もその軸の方向に分解して考えます。

このように分解して考えると、この放物運動の斜面に対して水平方向の運動は、初速度がV0cosφで加速度が-gsinθの等加速度直線運動となり、この放物運動の斜面に対して垂直な方向の運動は、初速度がV0sinφで加速度が-gcosθの等加速度直線運動となります。
このように斜面上で斜方投射をした場合は、斜面に対して水平の方向では等速直線運動とはならないので注意してください。
(3)解説授業の内容を復習しよう
①斜方投射
(4)平面内の運動の解説一覧
②相対速度の計算で間違えないために(電車の中から見た雨の角度と速度についても解説しています)
③等加速度直線運動の式の成り立ちと関係(v-tグラフの読み取り方、加速度・速度・変位の微分と積分の関係についても解説しています)
④放物運動の考え方(水平投射、斜方投射、斜面での斜方投射、飛行機から物体を落とす、台車から物体を打ち上げる)
(5)参考
☆物理の解説動画・授業動画一覧(力学・熱力学・波動・電磁気・原子)
☆物理に関する現象や技術(力学、熱力学、波動、電磁気、原子)
