対数微分法（問題と答え）【微分計算（数学Ⅲ）をマスターしよう】

【手順】

1. 両辺が正であることを確認する。正であることを確認できない場合は、両辺に絶対値をつける。（対数の真数は正でないといけないので）
2. 両辺の自然対数をとる。
3. 両辺をxで微分する。(logy)’=y’/yであることに注意（合成関数の微分）。
4. 両辺にyをかけて、y’=の形にする。yに元の式を代入するのを忘れないように！

【使いどころ】

1. 累乗の積や商で表された関数の微分
2. (xの式)^xの式のように指数で困ったとき

※対数にすることで、積が和に、商は差に、p乗はp倍にすることができることを利用する。対数の公式についてはこちら→対数（数学Ⅱ）公式一覧

【例題】

☆問題のみはこちら→対数微分法（問題）

☆微分法（数学Ⅲ）の計算公式一覧

---

①

【答案】

• まずは、両辺が正であることを確認するのを忘れないように！

②

【答案】

• x+3とxは正になるかは決まらないので、絶対値をつけるのを忘れないようにする。（x²+2は常に正であるので絶対値は不要）
• log(x²+2)の微分は合成関数の微分になることに注意
• (x+3)⁴の3乗根=(x+3)×(x+3)の3乗根

③以下の公式を証明せよ。ただし、αは実数である。

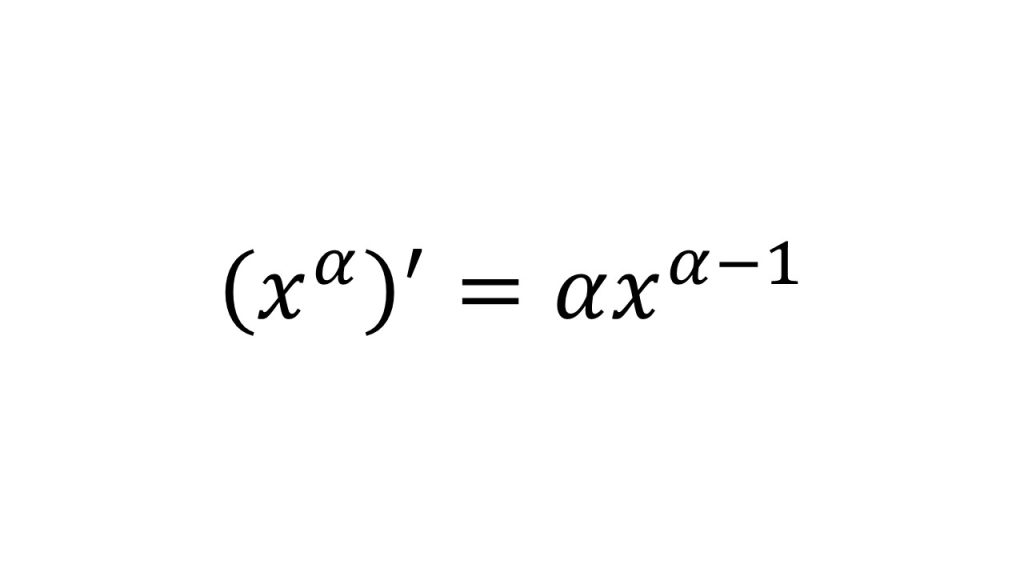
【証明】

• αが自然数でないときは二項定理を使って(x+h)^αを展開することができない。そのため、導関数の定義を使って証明することができない。
• xが正になるか決まらないので、絶対値をつけるのを忘れないようにする。

④以下の公式を証明せよ。

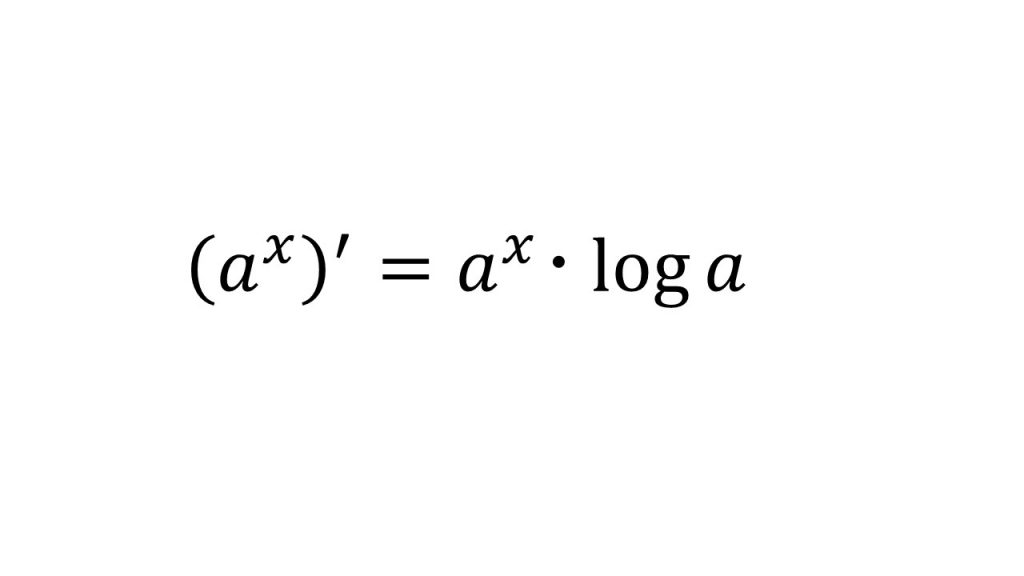
【証明】

• 導関数の定義では証明できないので、対数微分法を使って証明する。a^xが正になることの確認を忘れないようにする。

☆その他の計算公式の証明についてはこちら→微分（数学Ⅲ）の計算公式を証明しよう

---

☆問題のみはこちら→対数微分法（問題）

☆微分法（数学Ⅲ）の計算公式一覧

---

【微分計算（数学Ⅲ）の演習問題一覧】

①微分法（数学Ⅲ）の計算公式を使いこなそう！

②合成関数の微分法

③対数微分法

☆微分の計算公式の証明はこちら→微分（数学Ⅲ）の計算公式を証明しよう

～参考～

☆微分法（数学Ⅲ）の計算公式一覧

☆微分計算（数学Ⅲ）をマスターしよう（解説・授業・公式・演習問題一覧）

☆数学Ⅲ公式一覧

☆数学Ⅲの解説・授業・公式・演習問題一覧

☆数学の解説動画・授業動画一覧（Ⅰ・A・Ⅱ・B・Ⅲ）

☆数学公式一覧（Ⅰ・A・Ⅱ・B・Ⅲ）

☆数学の解説・授業・公式・演習問題一覧（Ⅰ・A・Ⅱ・B・Ⅲ）

☆数学典型パターン一覧（Ⅰ・A・Ⅱ・B・Ⅲ）

☆数学の語呂合わせ

☆数学学習に必要な参考書・問題集