(1)問題
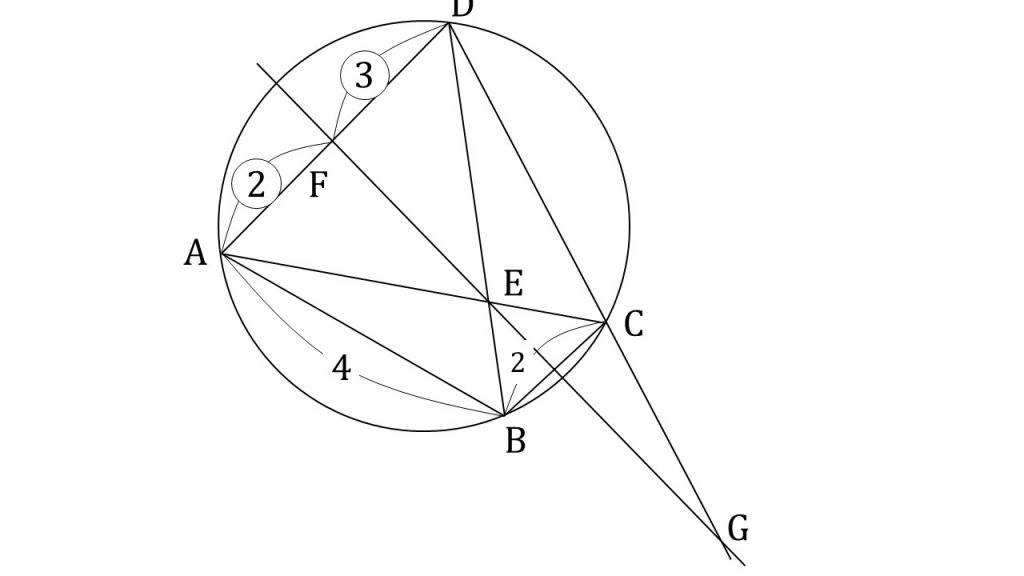
四角形ABCDにおいて、AB=4、BC=2、DA=DCであり、4つの頂点A, B, C, Dは同一円周上にある。対角線ACと対角線BDの交点をE、線分ADを2:3の比に内分する点をF、直線FEと直線DCの交点をGとする。
①∠DAC=∠DCA=∠DBC=∠DBAを示せ。
②AE:ECと、DG:GCを求めよ。
③直線ABが点Gを通る場合について考える。このとき、BGとDCの長さを求めよ。
(2016年センター試験本試験数学ⅠA第5問(1)より)
(2)答案
①

②

③


(3)解法のポイント
②辺の比を求める問題は、
ⅰ)角の二等分線の性質
ⅱ)チェバ・メネラウスの定理
ⅲ)方べきの定理
ⅳ)相似
ここらへんを選択肢として用意しておきましょう。
(4)必要な知識
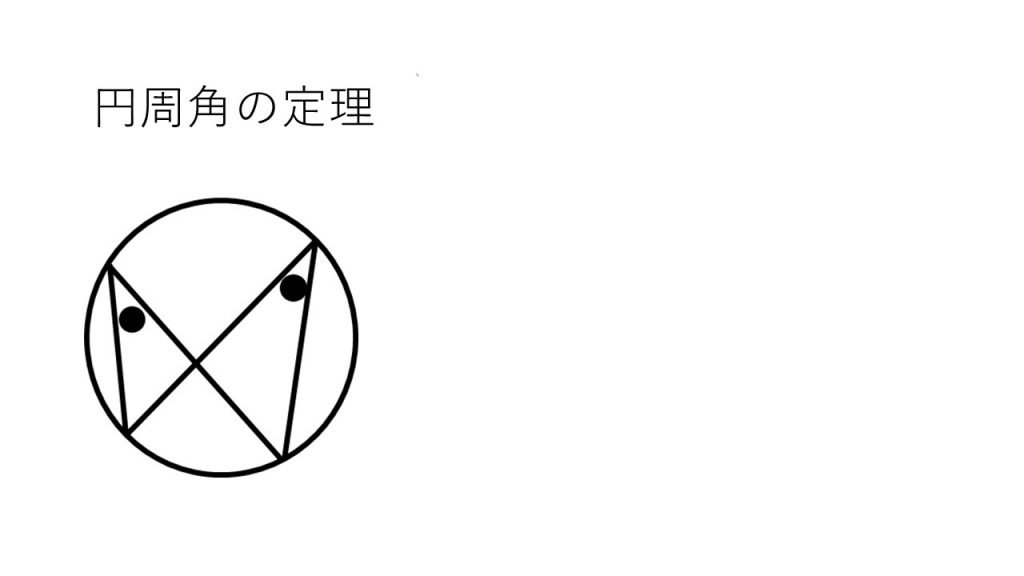
①円周角の定理
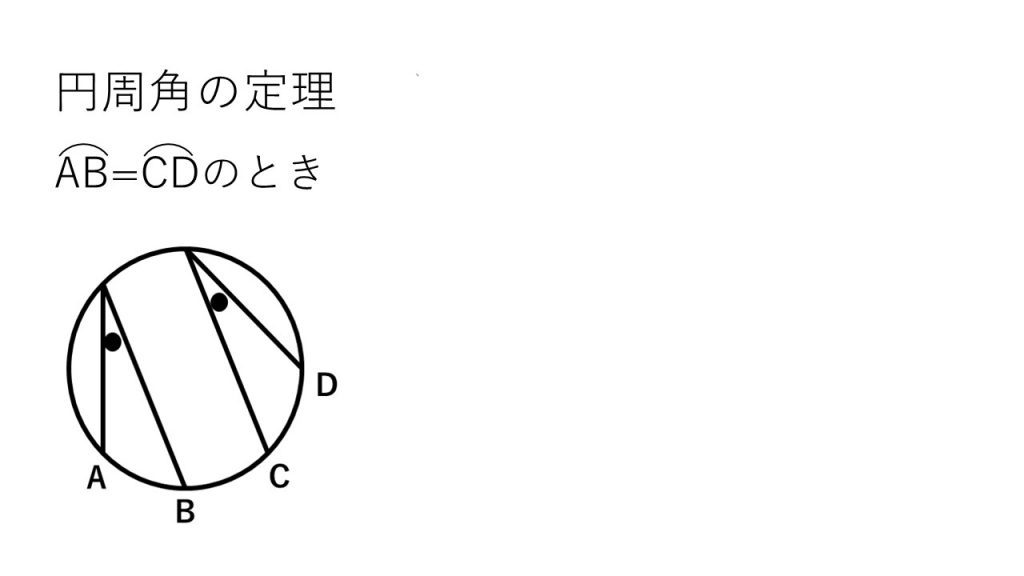
②三角形の角の二等分線の性質
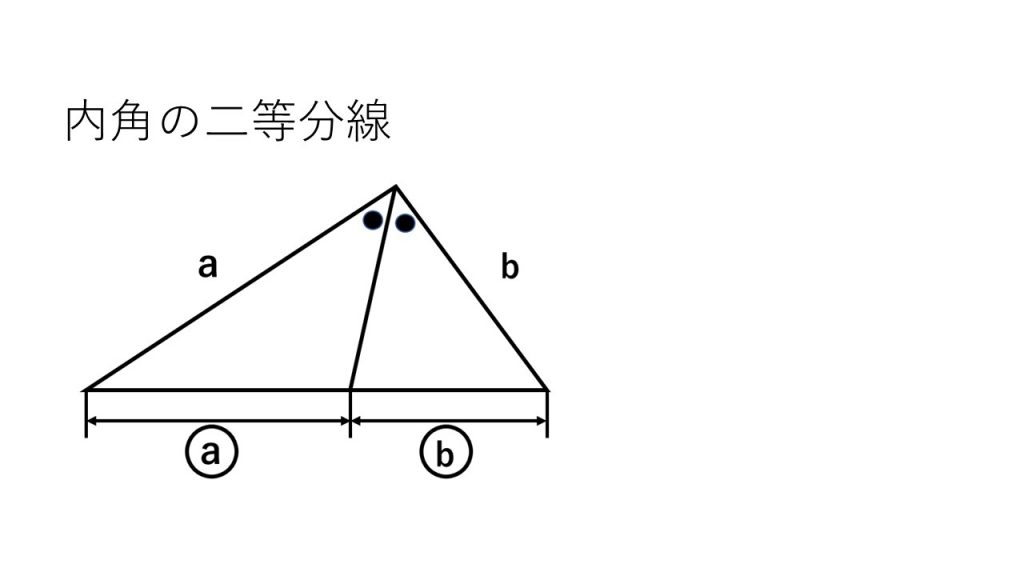
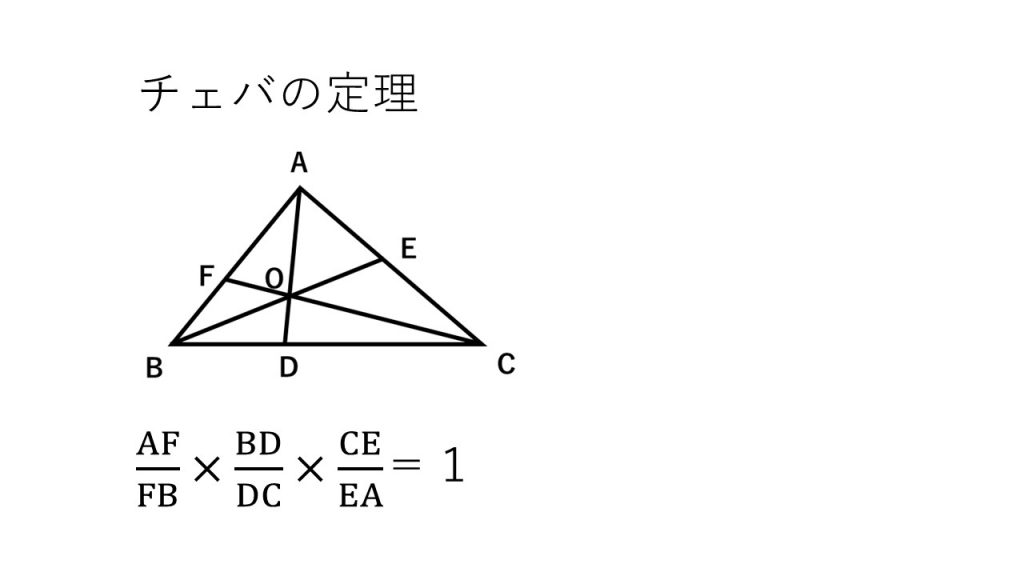
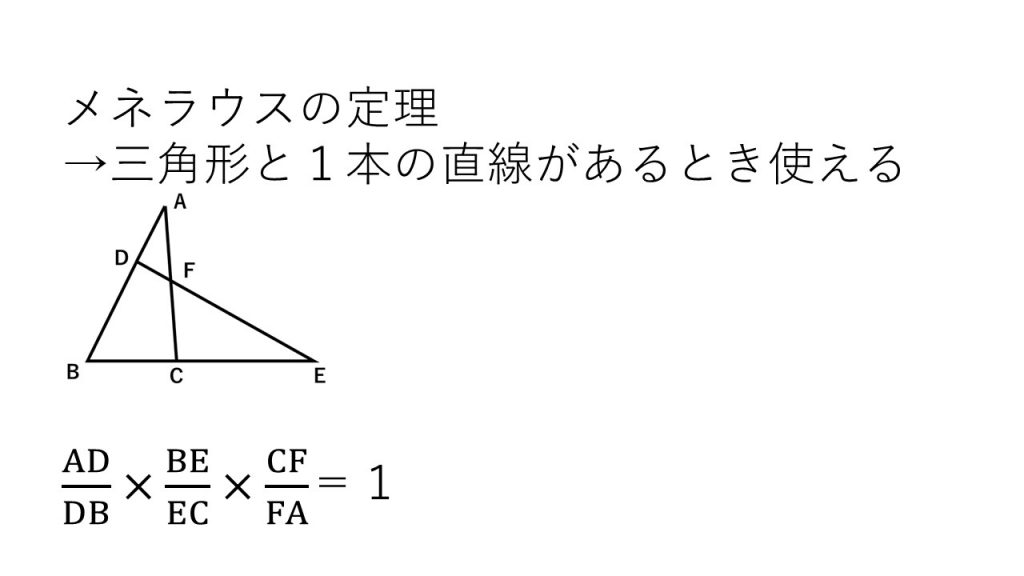
③チェバ・メネラウスの定理
④方べきの定理
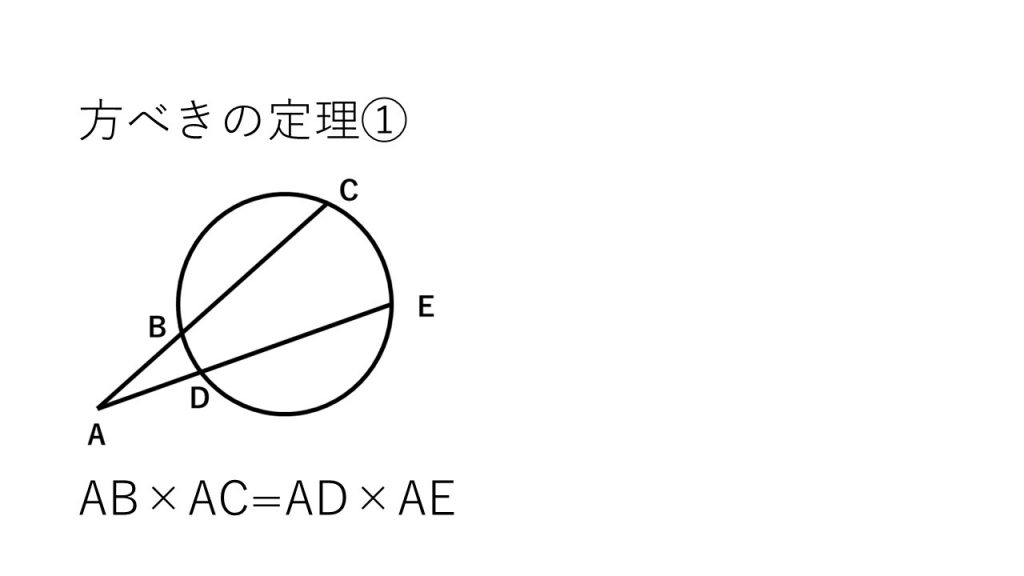
(5)理解すべきこと
チェバ・メネラウスの定理の簡単な使い方を知っておきましょう→チェバ・メネラウスの定理の簡単な使い方
☆動画はこちら↓
