合成関数の微分法（問題と答え）【微分計算（数学Ⅲ）をマスターしよう】

【使いどころ】

• y=f(g(x))をxで微分するとき。
• 簡単に言うと、関数の中に関数が入っているとき。

【正式な手順】

1. g(x)=uとする。（y=f(u)となる）
2. dy/duとdu/dxを求める。
3. dy/dx=dy/du・du/dxに代入して、dy/dxを求める。

※dy/dxは「yをxで微分する」という意味。よって、dy/duは「yをuで微分する」、du/dxは「uをxで微分する」という意味になる。

【実際に行う手順】

「全体の微分×中身の微分」と考える。

※dy/duが「全体の微分」に対応し、du/dxが「中身の微分」に対応する。

【例題】

☆問題のみはこちら→合成関数の微分法（問題）

☆微分法（数学Ⅲ）の計算公式一覧

---

①

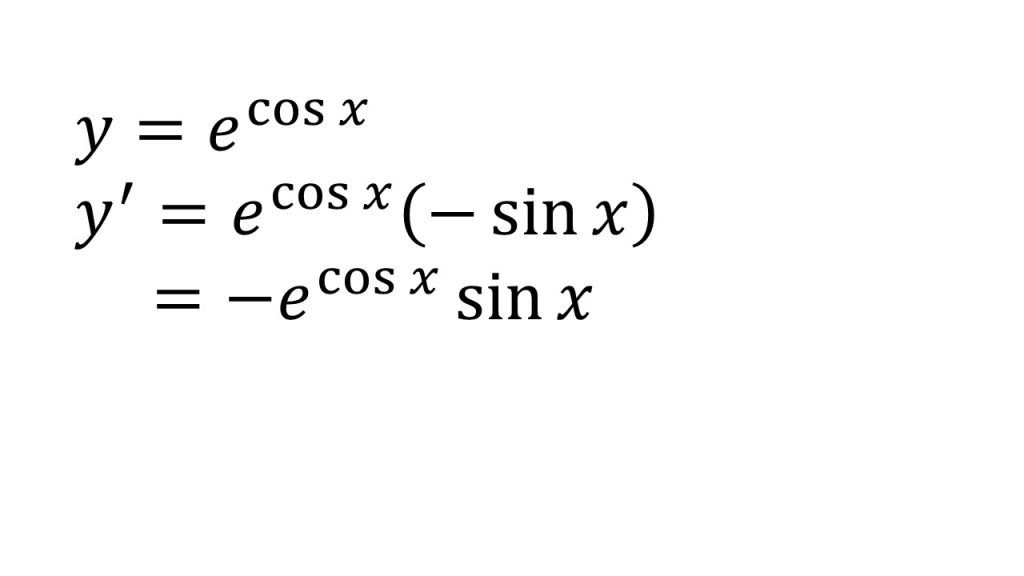
• e^uを全体、cosxを中身と考える。

②

• 積の微分を利用する。
• loguを全体、2x+3を中身と考える。

③

• 積の微分を利用する。
• loguを全体、sinxを中身と考える。

④

• 商の微分を利用する。
• sinuを全体、cosxを中身と考える。
• e^uを全体、3x+1を中身と考える。

⑤

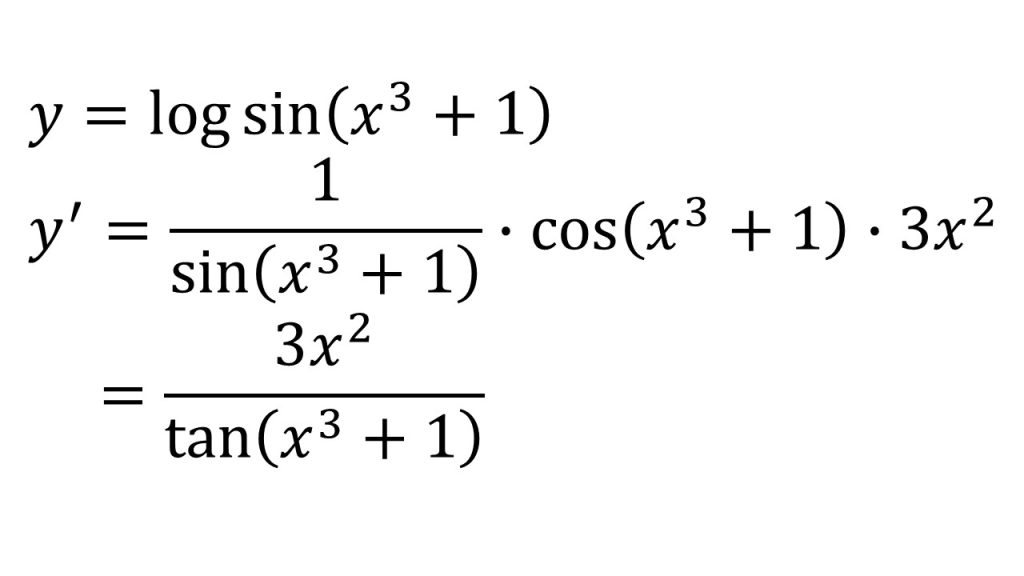
• 合成関数の微分を2回利用する。「全体の微分×中身の微分×中身の中身の微分」と考えるとよい。
• loguを全体、sinvを中身、x³+1を中身の中身と考える。

⑥

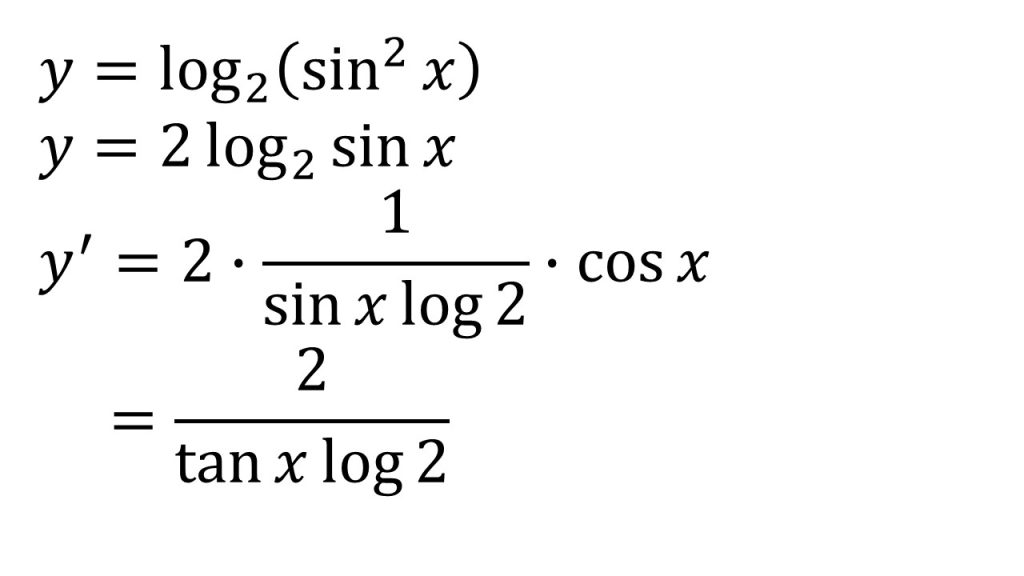
• logM^k=klogM
• log₂uを全体、sinxを中身と考える。
• tanx=sinx/cosx

⑦

• 3^uを全体、cosxを中身と考える。

---

☆問題のみはこちら→合成関数の微分法（問題）

☆微分法（数学Ⅲ）の計算公式一覧

---

【微分計算（数学Ⅲ）の演習問題一覧】

①微分法（数学Ⅲ）の計算公式を使いこなそう！

②合成関数の微分法

③対数微分法

☆微分の計算公式の証明はこちら→微分（数学Ⅲ）の計算公式を証明しよう

～参考～

☆微分法（数学Ⅲ）の計算公式一覧

☆微分計算（数学Ⅲ）をマスターしよう（解説・授業・公式・演習問題一覧）

☆数学Ⅲ公式一覧

☆数学Ⅲの解説・授業・公式・演習問題一覧

☆数学の解説動画・授業動画一覧（Ⅰ・A・Ⅱ・B・Ⅲ）

☆数学公式一覧（Ⅰ・A・Ⅱ・B・Ⅲ）

☆数学の解説・授業・公式・演習問題一覧（Ⅰ・A・Ⅱ・B・Ⅲ）

☆数学典型パターン一覧（Ⅰ・A・Ⅱ・B・Ⅲ）

☆数学の語呂合わせ

☆数学学習に必要な参考書・問題集