(1)例題
図aのように、十分大きくなめらかな円錐面が、中心軸を鉛直に、頂点Oを下にして置かれている。大きさの無視できる質量mの小物体が円錐面上を運動する。頂点Oにおいて円錐面と中心軸のなす角度をθとし、重力加速度の大きさをgとする。
図a
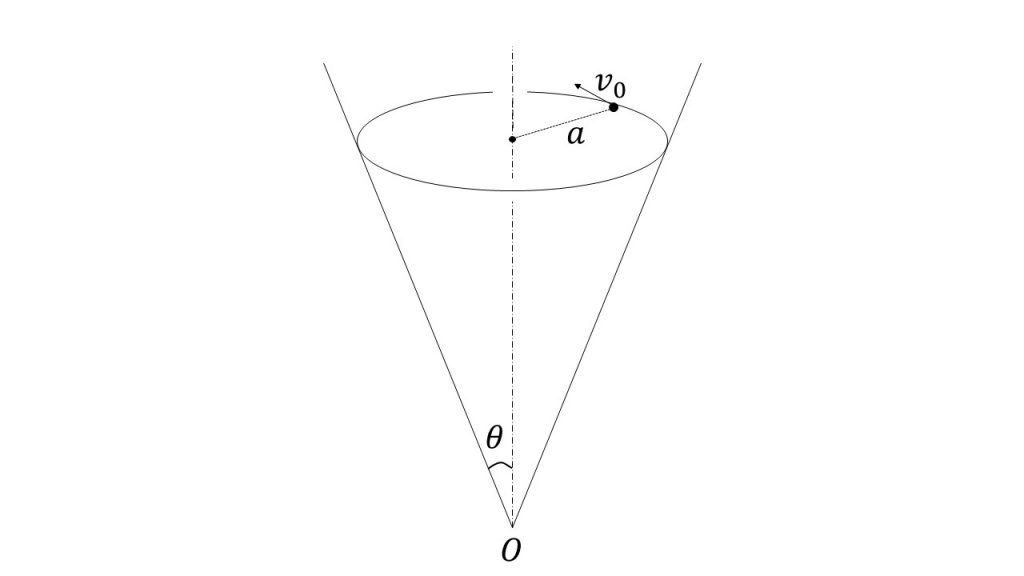
図bのように、大きさv0の初速度を水平方向に与えると、小物体は等速円運動をした。その半径rを表せ。
図b
(2017年センター試験本試物理第4問A問2)
(2)答案

(3)解法のポイント
円運動の問題の解法は、
①観測者を、物体とは離れた位置に置く→回転の中心方向の運動方程式+回転の中心方向と垂直な方向のつり合いの式
②観測者を、物体と一緒に回転させる→回転の中心方向のつりあいの式(遠心力を導入する)+回転の中心方向と垂直な方向のつり合いの式
のどちらかで取り組みます。
(4)必要な知識
①向心加速度

②向心力

③遠心力
→遠心力は慣性力(見かけの力)である。つまり、円運動している物体と一緒に回転しているときに向心力とは反対向きに引っ張られているように感じる力のことである。
④円運動の問題の取り組み方
ⅰ)観測者は円運動せずに、「ma=向心力」の運動方程式を考える。
ⅱ)観測者を一緒に円運動させることによって遠心力(慣性力)を導入して、つり合いの式を立てる(一緒に円運動している観測者にとっては物体は静止しているように見える)
⑤運動方程式

(5)理解すべきこと
等速円運動の問題の2つの解法について理解しましょう→等速円運動の2つの解法(向心力と遠心力についても解説しています)
☆動画はこちら↓
(6)参考
☆円運動の勉強法はこちら→円運動
☆力学の勉強法はこちら→力学の勉強法
