(1)例題

(2013年センター試験本試数学ⅠA第3問より)
(2)例題の答案
①

②

③

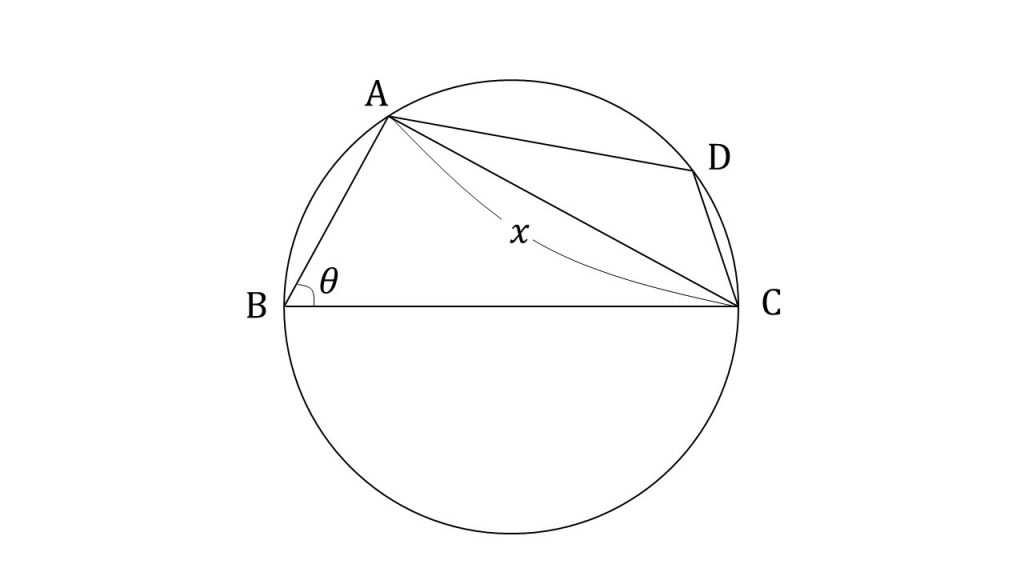
(3)解法のポイント
①円に内接する四角形は、向かい合う角の和が180°となることを使います。つまり、向かい合う角のコサインの値はプラスマイナスが逆のものであることを利用します(cos(180°ーθ)=-cosθを利用)
また、円に内接する四角形の問題で一番多いパターンは内角と対角線を求める問題です。解法の流れは、
ⅰ)それぞれを文字で置く
ⅱ)余弦定理を使って、方程式を2つ作って連立
となります。
③円に内接する四角形の向かい合う角のサインの値は同じです(sinθ=sin(180°-θ))
(4)必要な知識
①円に内接する四角形
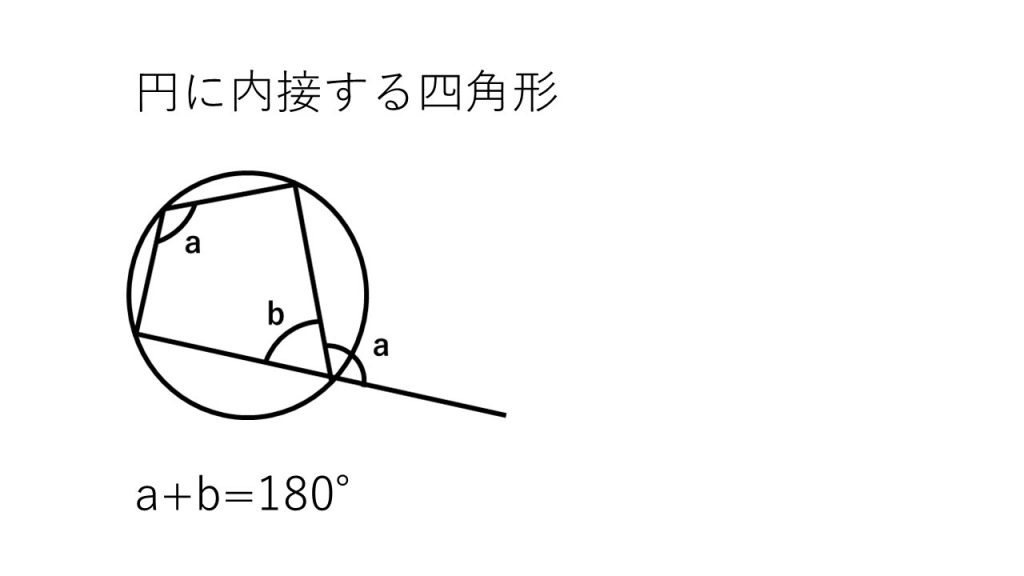
②180°-θの三角比
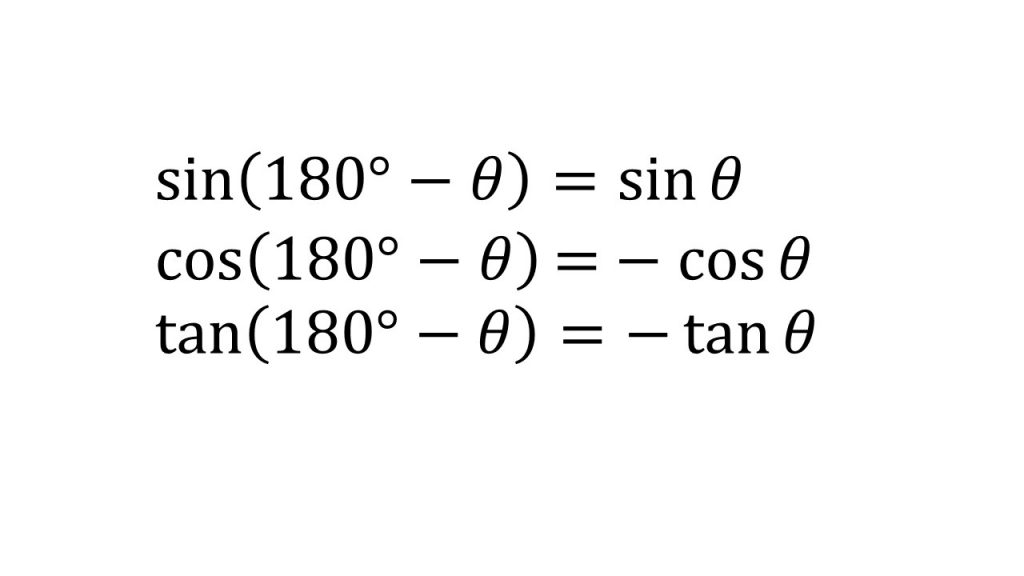
③正弦定理

④余弦定理

⑤三角形の面積の公式2つ

