(1)問題
△ABCにおいて、AB=3、BC=8、AC=7とする。また、△ABCの内心をIとする。
①頂点Aから辺BCに下した垂線AHの長さを求めよ。また、∠ABCを求めよ。
②△ABCの内接円と辺BC, CA, ABの接点をそれぞれP, Q, Rとしたとき、BPの長さを求めよ。
③△ABCの内接円の半径と、BIの長さを求めよ。
(2017年センター試験本試験数学ⅠA第5問(2)改)
(2)答案
①

-1024x576.jpg)
①三角比を使った答案

②

③

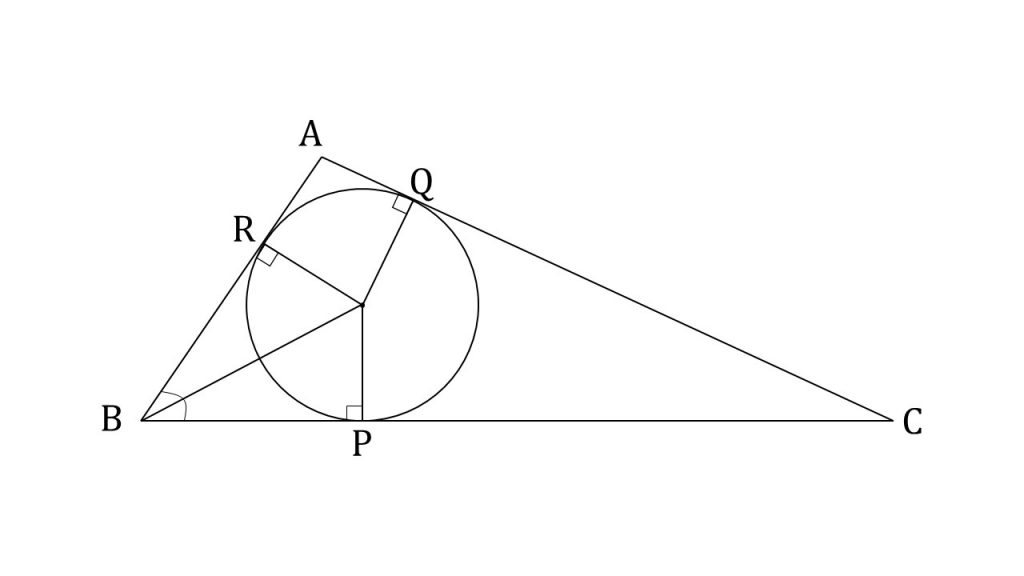
③三角比を使って内接円の半径を求める答案

(3)解法のポイント
①と②の答案の流れは頭に入れておきましょう。
①三平方の定理を使って、垂線の長さの2乗を2通りで表して、方程式を立てます。
②内接円の性質から、等しくなる長さを利用して方程式を立てます。イメージとしては、三角形をぐるっとまわって戻ってくるというイメージです。
また、角度や内接円の半径は三角比を用いて求められることも多いです。答案に行き詰った場合は、試してみるとよいでしょう。
(4)必要な知識
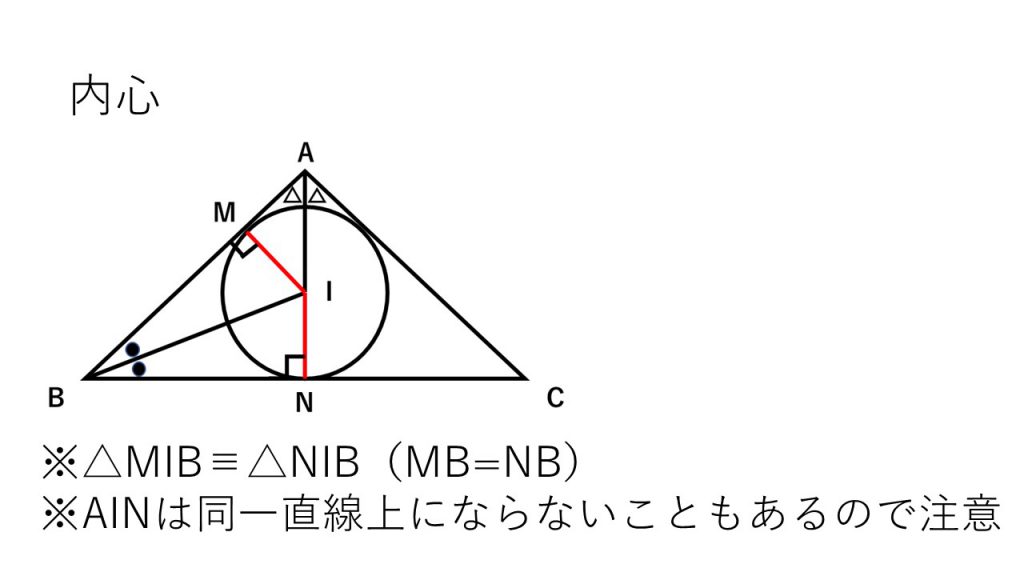
①内心
→定義:角の二等分線の交点
②余弦定理

③三角形の面積の公式2つ

