☆問題のみはこちら→三角関数の極限(数学Ⅲ)をマスターしよう!(問題)
(1)まずは公式を証明しよう

【証明】

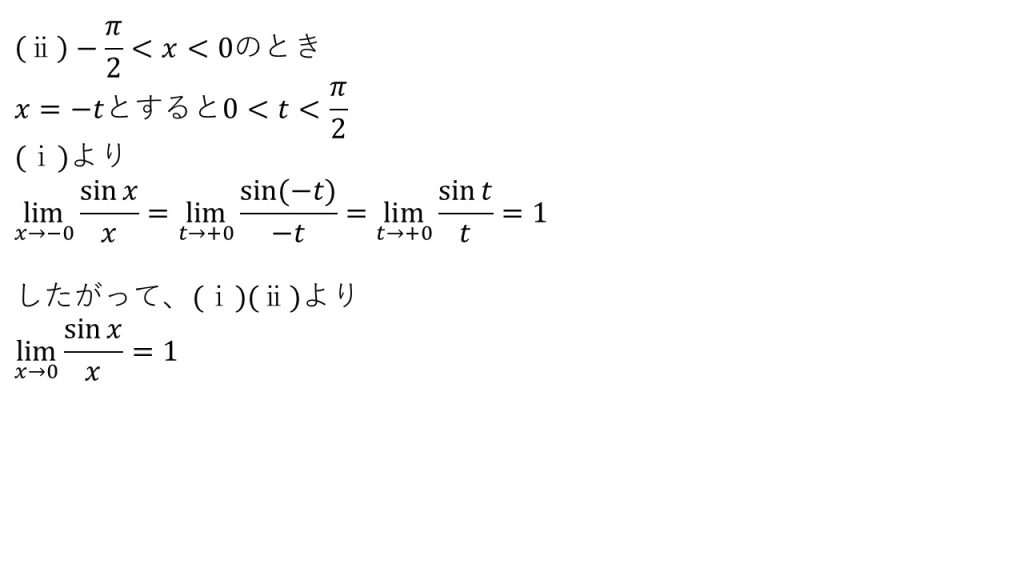
- (ⅰ)で右側極限が1になることを示し、(ⅱ)で左側極限が1になることを示している。
- ちなみに、単位円であれば、弧ABの長さがxになるが、xが十分に小さいとき、AB≒弧AB≒ACとなる(上の図で、xを小さくしていくとABと弧ABとACがどんどん近づいていく)。つまり、xが十分に小さいとき、sinx≒x≒tanxとなる。この近似は物理でよく用いられるので知っておくとよい。
(2)演習問題
①
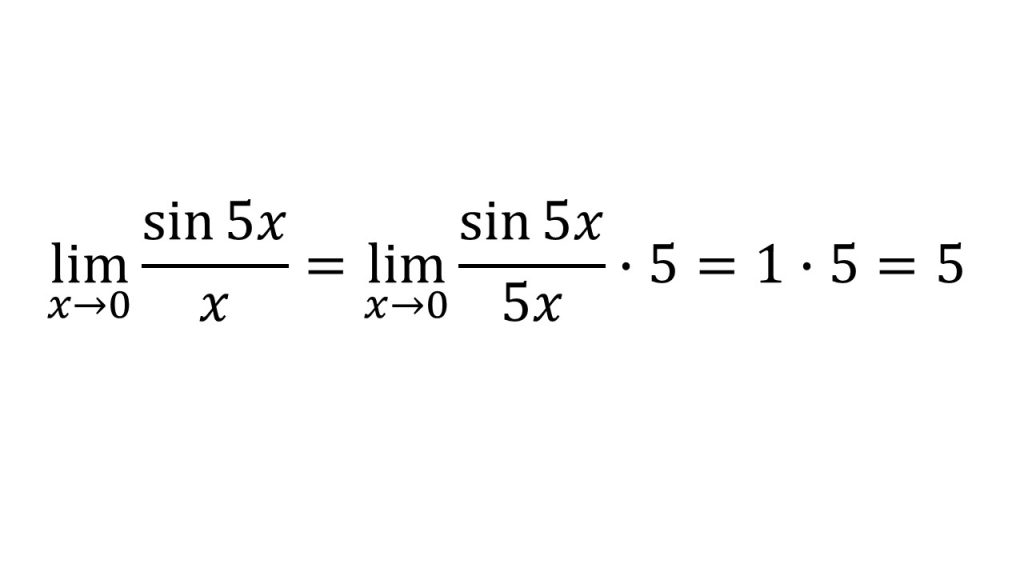
- 三角関数の極限のポイントは、sin〇/〇の〇の部分をそろえることである。
②
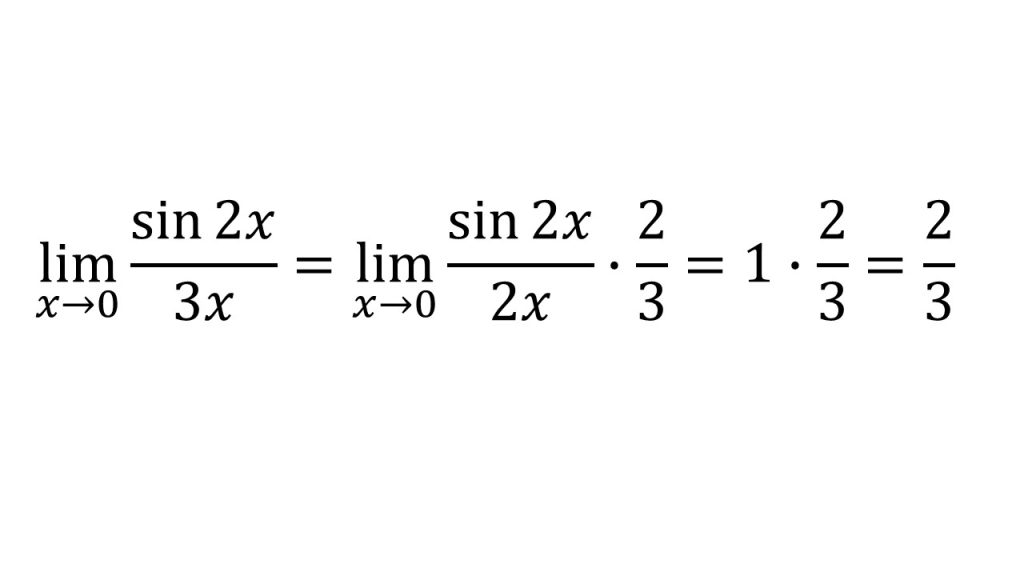
- 三角関数の極限のポイントは、sin〇/〇の〇の部分をそろえることである。
③

- x/sinxの極限も1になることは知っておこう。
④

- tanx/xの極限も1になることは知っておこう。(xが十分に小さいとき、sinx≒x≒tanxとなる近似からも理解することができる。)
⑤
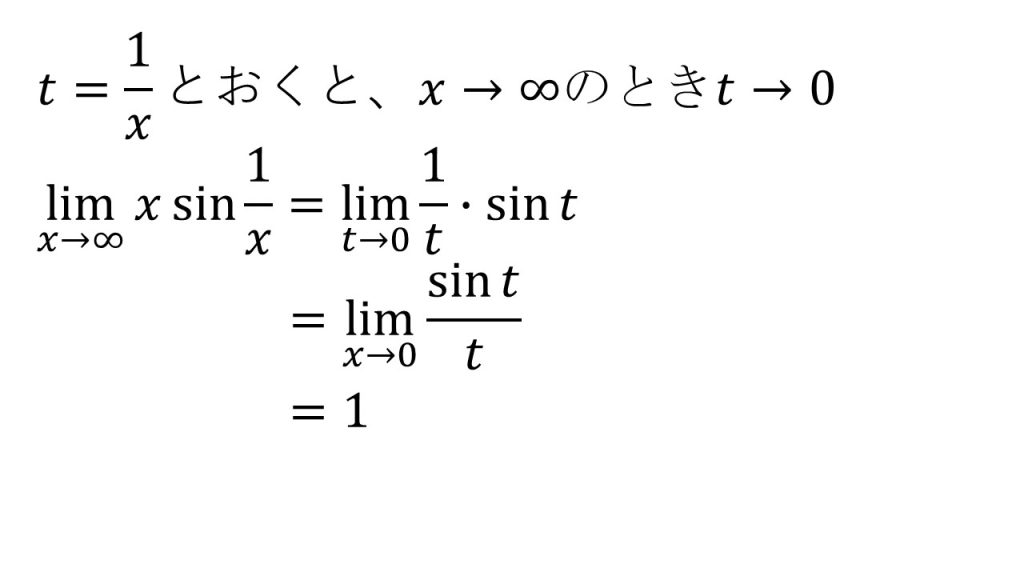
- x→∞となっていることに注意。三角関数の極限は→0でないと使えないので、t→0となるように置き換えをする。
⑥
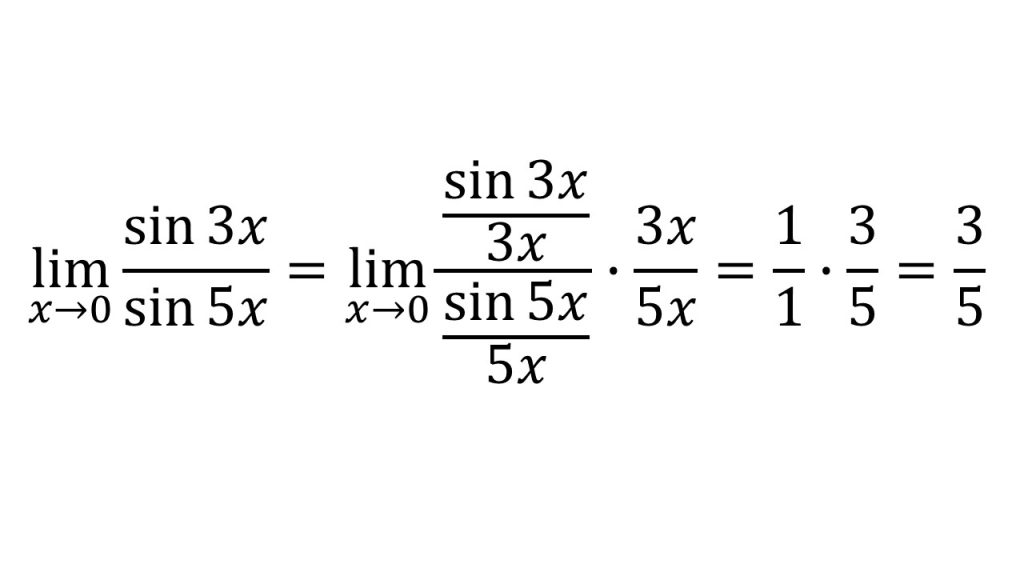
- 三角関数の極限のポイントは、sin〇/〇の〇の部分をそろえることである。
⑦
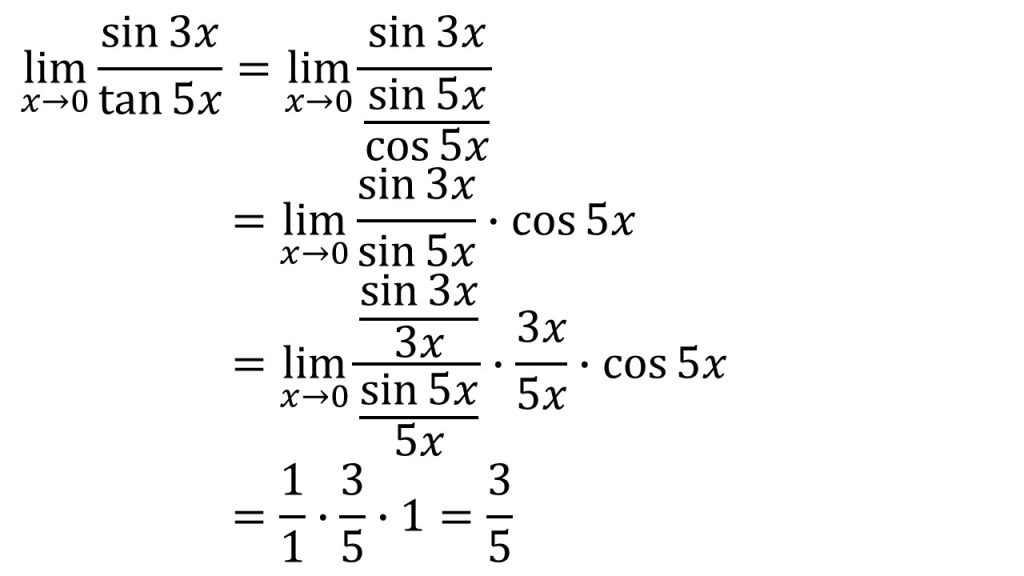
- 三角関数の極限のポイントは、sin〇/〇の〇の部分をそろえることである。
⑧
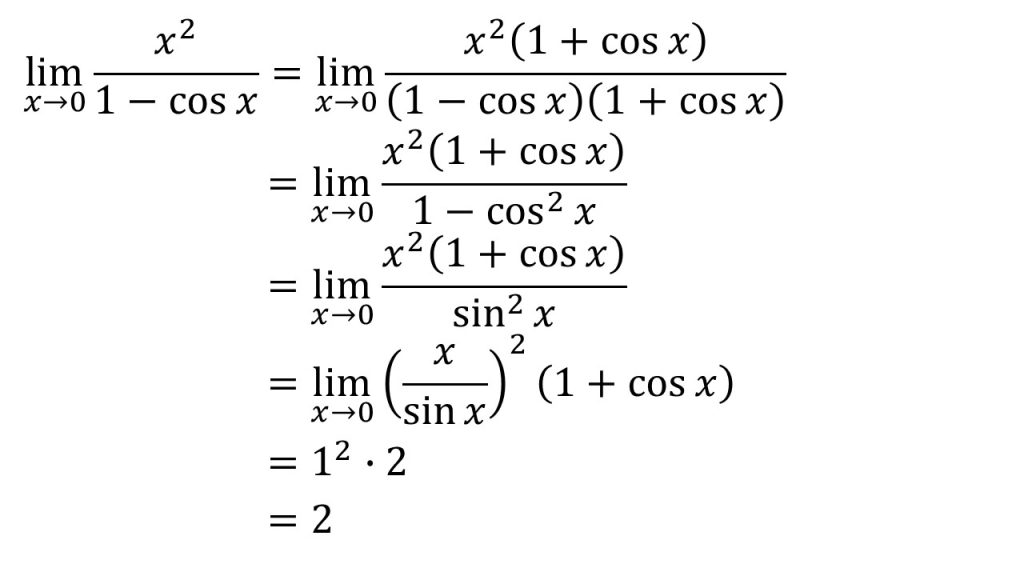
- 三角関数の極限の公式を用いるためにはsinxが必要である。そのため、「sinxを作ろう」という発想で式変形をする。
- sin2x+cos2x=1の利用
⑨
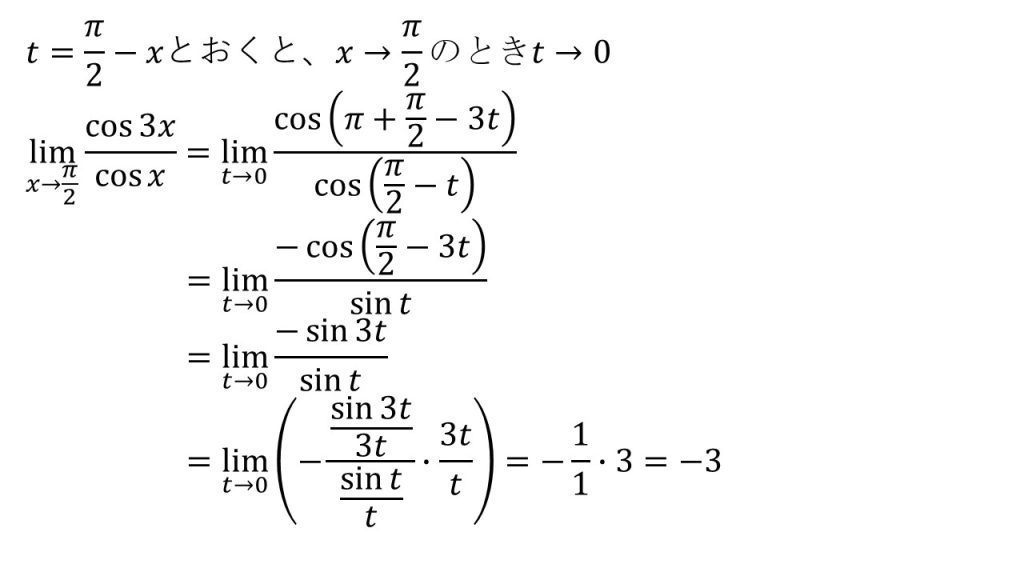
- 三角関数の極限の公式を用いるためにはsinxが必要である。そのため、「sinxを作ろう」という発想で式変形をする。
- x→π/2となっているので、t→0となるように置き換えをする。
- 以上の発想から、con(π/2-x)=sinxの利用を考える。
- cos(π+θ)=-cosθも利用している。
⑩
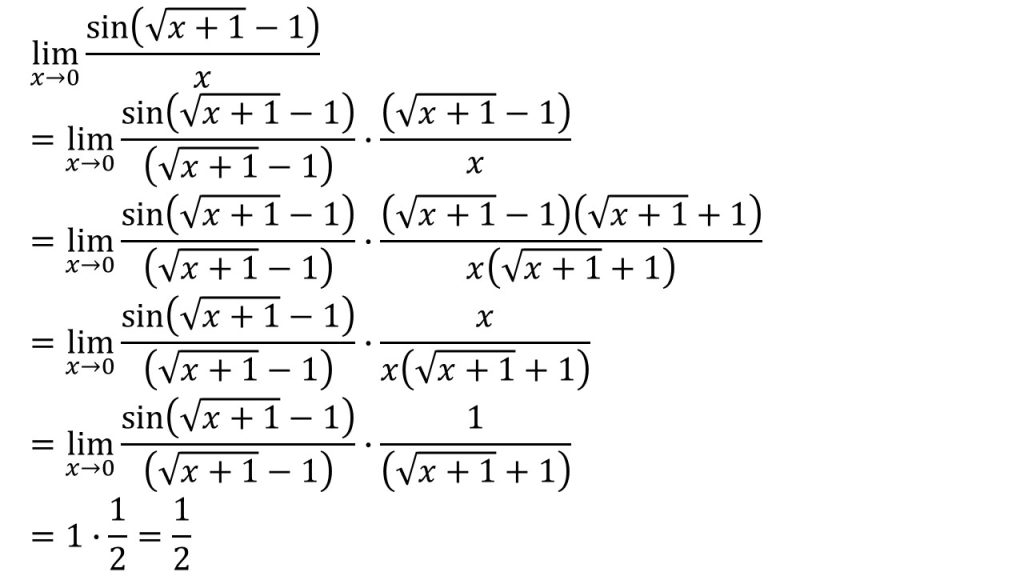
- 三角関数の極限のポイントは、sin〇/〇の〇の部分をそろえることである。
- √を含む式の極限を考えるときの基本として、逆有理化をする。
☆問題のみはこちら→三角関数の極限(数学Ⅲ)をマスターしよう!(問題)
