(1)例題
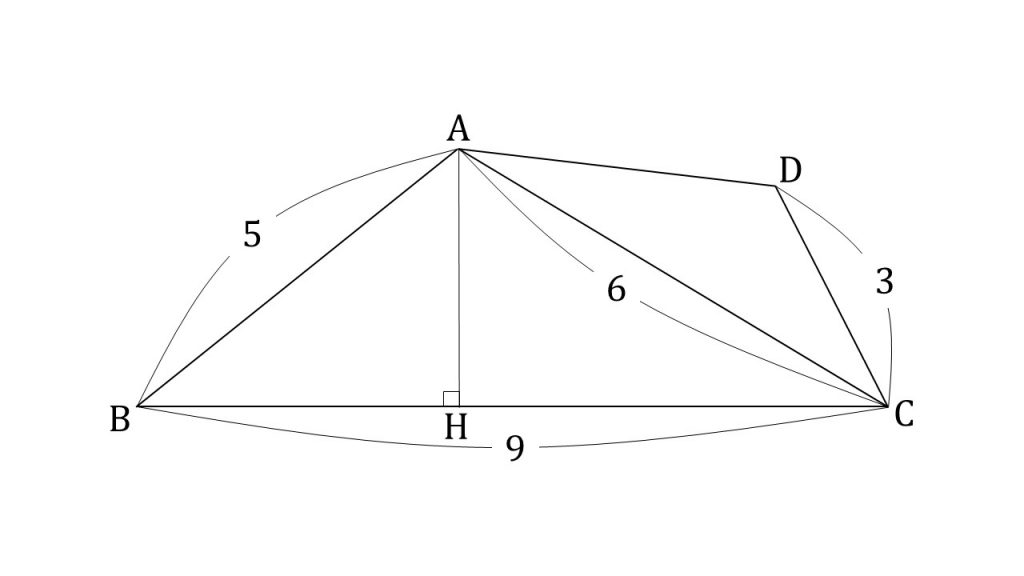
四角形ABCDにおいて、3辺の長さをそれぞれAB=5, BC=9, CD=3、対角線ACの長さをAC=6とする。
①cos∠ABC, sin∠ABCを求めよ。
四角形ABCDは台形であるとする。
②頂点AからBCに下した垂線の足をHとするとき、AHの長さを求めよ。
③AD//BCとAB//CDのどちらが成り立っているか。
④BDの長さを求めよ。
(2018年センター試験本試数学ⅠA第2問〔1〕)
(2)例題の答案
①

②

③

④

(3)解法のポイント
②直角三角形ができるときは、正弦定理や余弦定理ではなく、
底辺=斜辺×cosθ
高さ=斜辺×sinθ
高さ=底辺×tanθ
を利用しましょう。その方が早くてラクです。
③②の結果を使うという発想ができるかがポイントです。また台形であることは確定しているので、どちらかが平行でなければ、もう1つが平行であるということになります。
(4)必要な知識
①直角三角形と三角比

②三角比の相互関係の3つの式

③180°-θ、90°-θ、90°+θの三角比
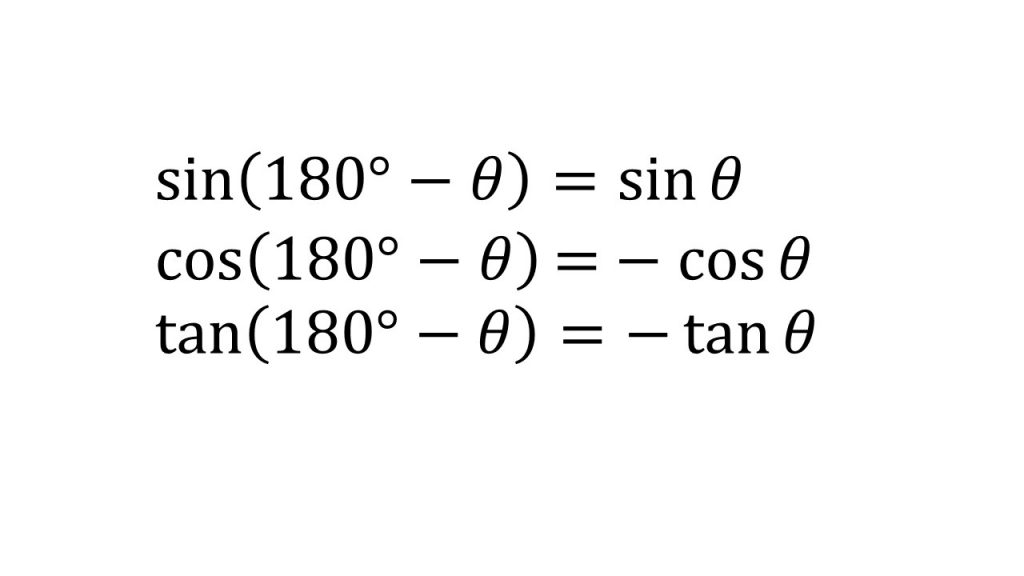
④余弦定理

