(1)例題
次の文章を読み,下の問いに答えよ。
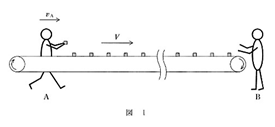
媒質中を伝わる波動を、ベルトコンベアによる物品の搬送と対応させて、ドッブラー効果を考えてみよう。図1のように十分に長いベルトコンベアがあり、上に乗せたものを一定の速さVで右に運んでいる。左側にいる作業者Aは、一定の速さ vAで作業者Bに向かって移動しながら、 一定の時間間隔T0で小さな箱をベルトコンベアの上に乗せていく。右側の作業者Bは、 運ばれてくる箱をベルトコンベアの端で回収す る。ただし、vA<Vとする。
①次の文章中の空欄[ ア ]・[ イ ]に入れる式を答えよ。
作業者Aが静止している場合(vA= 0)は、ベルトコンベア上の箱の間隔はT0Vであるが,動いている場合(vA≠ 0)は、箱の間隔はd=[ ア ]となる。このとき、静止している作業者Bが箱を受け取る時間間隔はT=[ イ ]である。
②次の文中の空欄[ ウ ]~[ オ ]に入れる語を、{波長・振動数・速さ}から選べ。
作業者A,Bをそれぞれ波源と観測者にみたてて、ドップラー効果との対応を考えてみよう。箱の位置を波の山の位置、作業者Aが箱をおく時間間隔T0を波源での波の周期、箱の速さVを波の速さとみなすと、ベルトコンベア上にならぶ箱の間隔dは観測される波の[ ウ ]、作業者Bが箱を受け取る時間間隔Tは観測される波の周期と解釈できる。 波源が運動してドップラー効果が起きているときは、波の[ エ ]は変わらず、[ オ ]が変化する。ベルトコンベアの搬送は波動とは異なる現象であるが、上記のように考えると、ドップラー効果を理解することができる。
(センター試験2014年本試物理Ⅰ第3問Aより)
(2)例題の答案
①[ ア ]
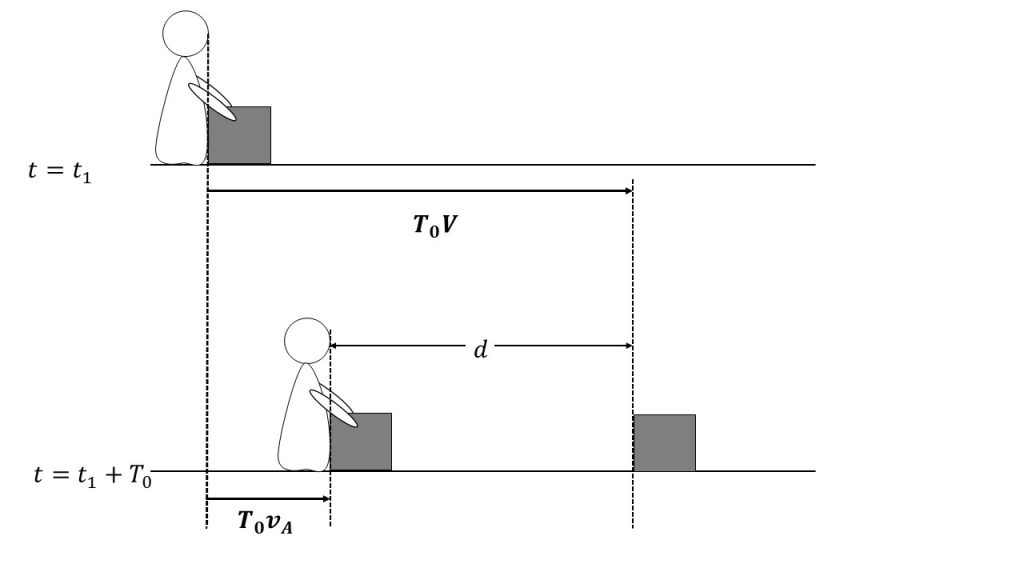
作業者Aが1つ目の箱を乗せた時刻t=t1から、2つ目の箱を乗せた時刻t=t1+T0までの間に、1つ目の箱はベルトコンベアとともに床に対して距離T0V動き、作業者Aは床に対して距離 T0vA動く。したがって、箱の間隔dは
d = T0V - T0vA =T0(V- vA)
[ イ ]
作業者Bに向かって動いてくる箱の速さは、ベルトコンベアの速さに等しくVであり、箱は間隔dで動いてくるから、作業者Bが箱を受け取る時間間隔は
T=d/V
②[ ウ ]:波長、[ エ ]:速さ、[ オ ]:振動数
(3)解法のポイント
ドップラー効果の原理を理解することができる良問です。
重要なことは、ベルトコンベアの速さが一定であるように、空気中を伝わる音の速さは変わらないということです。
また、作業者Aが箱を置く時間間隔も一定であるように、音源での振動数は変化しないということも重要です。
ゆえに、作業者Aが近づくにつれて箱と箱の間隔が狭くなるように、音源が観測者に近づくにつれて波長が短くなり、観測者は振動数が変化したように感じるというわけです。
ドップラー効果の問題を考えるときは、このようにベルトコンベアと箱のモデルで考えるようにすると、確実に問題が解けるようになります。
(4)必要な知識
①ドップラー効果

(5)理解すべきこと
