(1)解説授業動画
☆YouTubeチャンネルの登録をよろしくお願いします→大学受験の王道チャンネル
(2)解説授業の原稿
ドップラー効果とは何か
ドップラー効果について解説します。
ドップラー効果とは音源または観測者が動くことで、音波の振動数が変化して聞こえる現象のことです。
音波の振動数が変化するということは音の高さが変わるということなので、音源と観測者が静止しているときよりも音が高く聞こえたり低く聞こえたりします。
ドップラー効果の式
それではドップラー効果が発生したとき、観測者が観測する音の振動数がどのようになるかの式を確認します。
音源の振動数をf、音速をVとし、音源の速度をvs、観測者の速度をvoとします。ちなみに、音源を英語でsource、観測者を英語でobserverというので音源の速度をvs、観測者の速度をvoとしています。
まず、観測者は動かずに音源だけが動いている場合は、観測者が観測する振動数は
f1=V/(Vーvs)・f
となります。そして、音源は動かずに観測者だけが動くとき、観測者が観測する音の振動数は
f2=(Vーvo) /V・f
となり、音源も観測者も両方動くときの観測者が観測する振動数は
f’=(Vーvo)/(Vーvs)・f
となります。
音源の振動数と空気中の音速は変わらない
これらの式に関していくつかポイントがあります。まず、音源が出す音の振動数は一定であるということです。これは波の問題を考えるときに常に気を付けてほしいことなのですが、音源や波源の振動数はその音源や波源自体を変えない限り変化することはありません。
そして、空気中の音速も変化することはありません。空気中の音速は温度を変えない限り変化しないので、ドップラー効果の問題を考えるときは、空気中の音速自体が変化することはないと考えてください。
あくまでドップラー効果で変化しているのは観測者が観測する振動数です。音源自体の振動数や空気中の音速自体は変わることがないので注意しましょう。
vsとvoの正負に注意
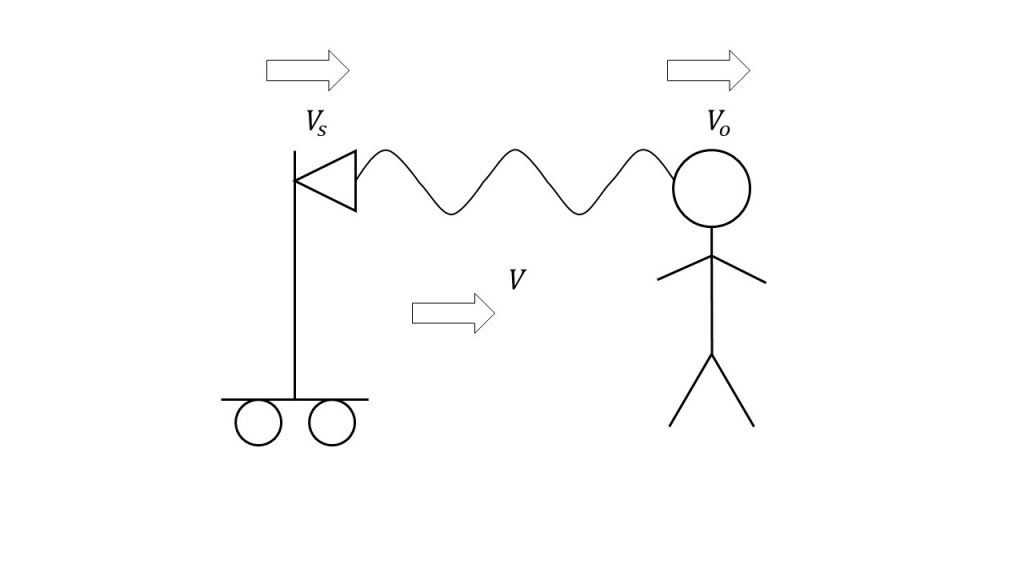
また、もう1点注意したいことは、vsとvoは、音源から観測者に向かう向きを正とします。下図でいえば、右向きが正となります。
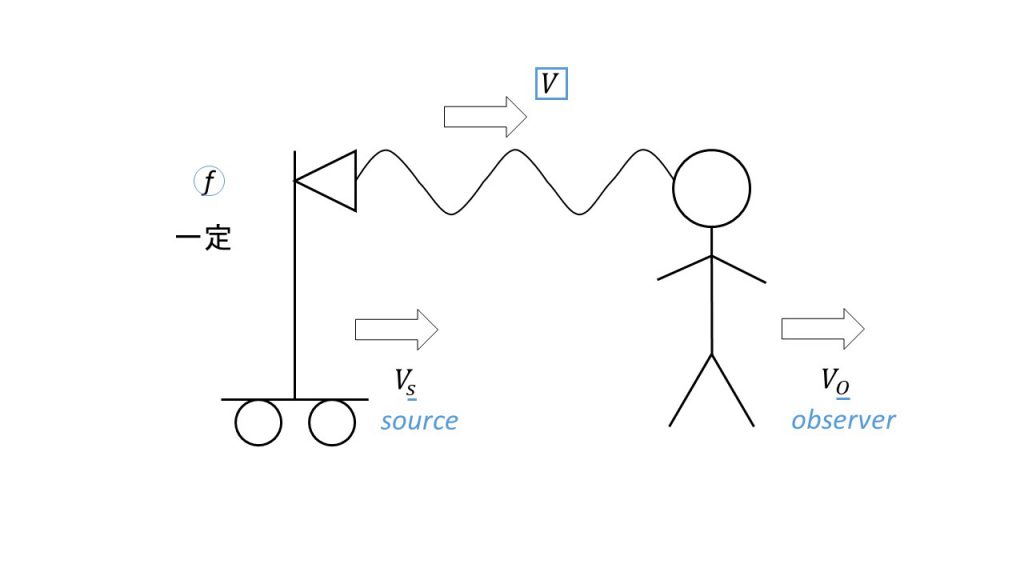
そのため音源が観測者に近づいてきているときは符号はそのままでいいのですが、例えば音源がvsの速さで左側に遠ざかっているときは、このvsにーvsを代入するので
f1=V/(V+vs)・f
となります。このようにvsとvoは向きに注意して正負を間違えないようにしましょう。
ドップラー効果の一般的な式
そして、f’=(Vーvo)/(Vーvs)・fの式のvoを0とすれば、f1の式となり、vsを0とすればf2の式となります。つまりこのf’の式がドップラー効果の一般的な式といえます。
そのため問題を解くときは、f’=(Vーvo)/(Vーvs)・fの式を使ってvsとvoに適切な値を代入することで問題を解くことができます。
それではなぜこのような式になるのか考えていきます。
ベルトコンベアによるドップラー効果のモデル
ドップラー効果の式の導出を考える前に、ドップラー効果がより理解しやすくなる例えがあるのでまずはそちらをご紹介します。
それはベルトコンベアによるドップラー効果のモデルです。
例えば、下図のように一定の速さで動くベルトコンベアがあり、左側にベルトコンベアに荷物を置く人がおり、ベルトコンベアを流れてくる荷物を受け取る人が右側にいるとします。荷物を置く人は一定のリズムで荷物を置きます。

一番上の図のように荷物を置く人も荷物を受け取る人も停止していれば、荷物と荷物の間の距離は常に一定であり、荷物を受け取る人も一定の間隔で荷物を受け取ることになります。
次に、真ん中の図のように荷物を受け取る人は動かずに、荷物を置く人が近づきながら荷物を置いたとしましょう。この場合、荷物と荷物の間隔は、荷物を置く人が動かないときよりも狭くなります。すると、荷物を受け取る人が1秒間に受け取る荷物の個数は増えることになります。
そして次に、一番下の図のように荷物を置く人は動かずに荷物を受け取る人が離れながら荷物を受け取ったとしましょう。この場合、荷物と荷物の間隔は、一番上の図のときと等しくなります。しかし、受け取る人が離れていっているので、荷物を受け取る人が1秒間に受けとる荷物の個数は減少することになります。
ベルトコンベアのモデルが表していること
つまり、このベルトコンベアのモデルにおいて、1秒間に荷物を置く個数は音源の振動数を表しており、ベルトコンベアの速さは空気中の音速を表しています。そして、荷物の間隔は波長を表しており、1秒間に荷物を受け取る個数が観測者が観測する振動数を表しています。
したがって、荷物を置く人が近づけば1秒間に受け取る荷物の個数が増えたように、音源が近づけば観測者が観測する振動数は増加し、高い音が聞こえるということになります。
また、荷物を受け取る人が遠ざかっていけば1秒間に受け取る荷物の個数が減ったように、観測者が音源から遠ざかっていく場合は観測者が観測する振動数は減少し、低い音が聞こえるということになります。
ベルトコンベアの速さ(=空気中の音速)は一定である
そして、このベルトコンベアのモデルで重要なことは、ベルトコンベアの速さは、たとえ荷物を置く人や荷物を受け取る人が動いたとしても一定であるということです。
そのため、1度置かれた荷物は一定の速さで移動します。したがって、荷物を置いたときに荷物の間隔が狭くなったとしても、その間隔のまま受け取る人のところに届きます。
それは受け取る人が動いていても同様です。たとえ受け取る人が動いていたとしても荷物の間隔自体は荷物を置いたときと変わることなく届きます。
ゆえに荷物を置く人にとっての荷物の間隔と、荷物を受け取る人にとっての荷物の間隔は等しくなります。そして荷物の間隔は波長のことなので、音源にとっての波長と観測者にとっての波長は等しくなるということになります。
このことがドップラー効果の式を導出するときに重要になります。
ドップラー効果の式を導く
それではドップラー効果の式を導いてみます。
波の基本式
その前にまず波の基本式を確認すると、波の基本式は
v=fλ
であり、λ=の形にすると、
λ=v/f
となります。
音源が動くとき
観測者は動かずに音源が動くときの、音源にとっての音速、振動数、波長、そして観測者にとっての音速、振動数、波長を考えてみます。最初に確認したとおり、音源から観測者に向かう向きを正とします。
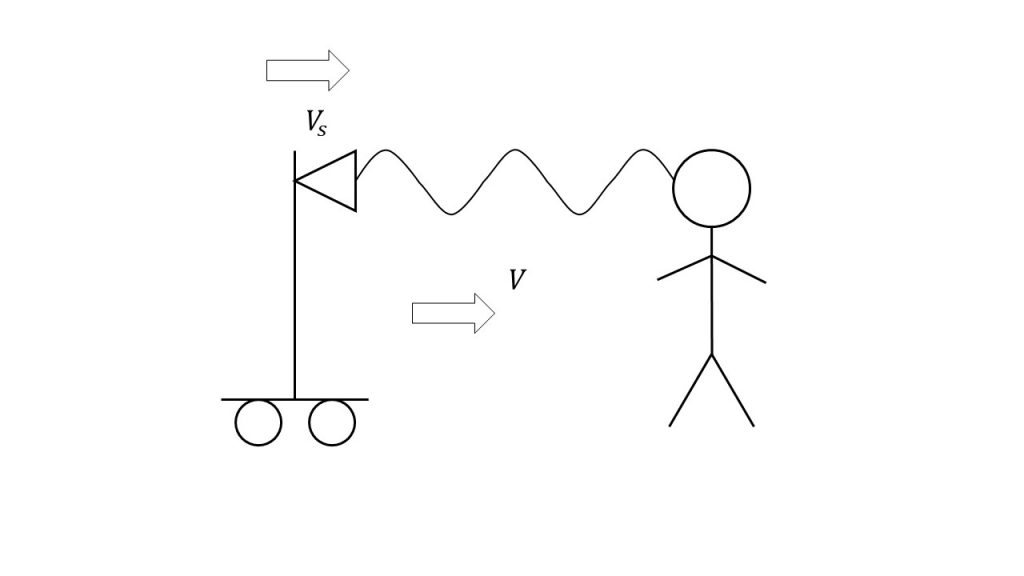
このとき、音源にとっての音速は音源自体がvsの速度で動いているので、V-vsとなります。これは相対速度の考え方を使っています。
次に、音源にとっての振動数は最初に確認したとおり、常に変わることはありません。
そして、音源にとっての波長は、先ほどのベルトコンベアの例のように音源が動くことで変化します。
次に、観測者にとっての音速は動いていないのでVとなります。
また、観測者にとっての振動数は、受け取る波の波長が変化しているので振動数も変化します。
そして、観測者にとっての波長は先ほども確認した通り、音源にとっての波長と等しくなります。
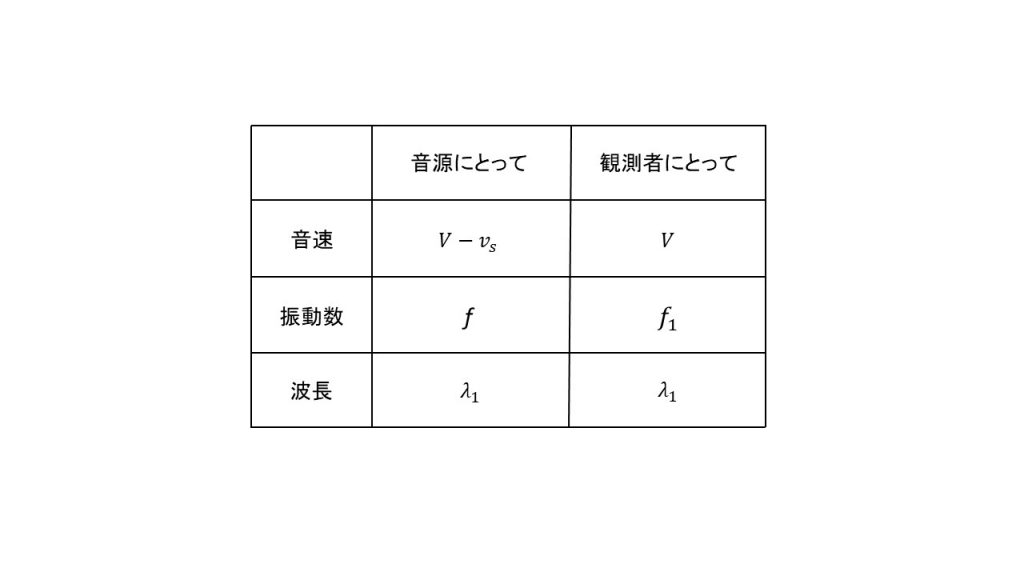
よって、音源にとっての波の基本式は
λ1=(Vーvs)/f
となり、観測者にとっての波の基本式は
λ1=V/f1
となります。ゆえに
(Vーvs)/f=V/f1
の等式が成り立ち、f1=の形にすると、
f1=V/( Vーvs)・f
音源が動くときのドップラー効果の式となります。
観測者が動くとき
同様にして音源は動かずに観測者が動くときのドップラー効果の式を導いてみます。
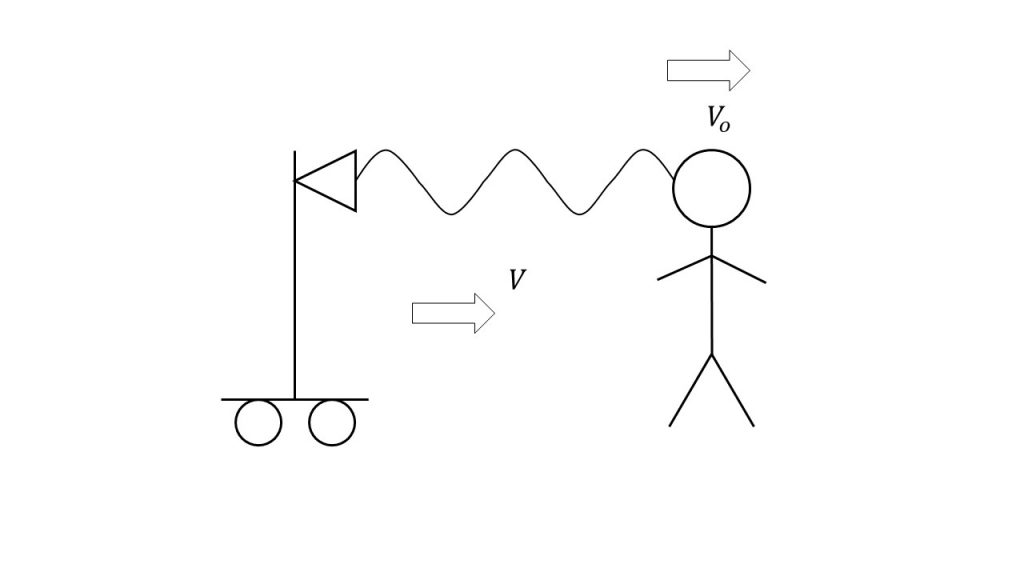
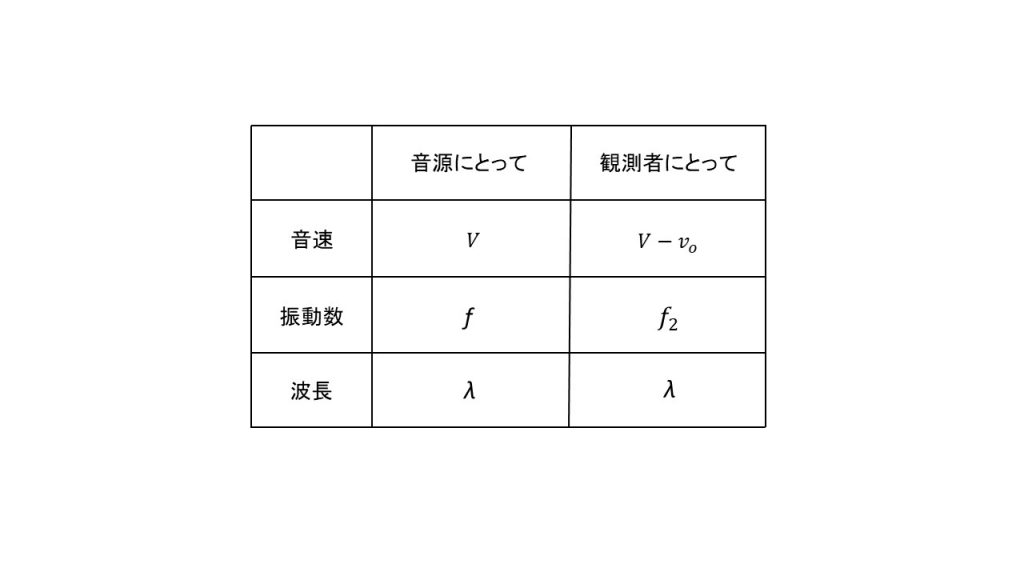
このとき、音源にとっての音速は音源が動いていないのでVとなります。
また、音源にとっての振動数はやはり変わることはなくfになります。
そして、音源にとっての波長は、音源が動いていないので変化はありません。
次に、観測者にとっての音速ですが、観測者は動いているので相対速度の考え方を使って、Vーvoとなります。
また、観測者にとっての振動数は、観測者が動くことによって変化します。
そして、観測者にとっての波長はやはり音源にとっての波長と等しくなります。
よって、音源にとっての波の基本式は
λ=V/f
となり、観測者にとっての波の基本式は
λ=(Vーvo)/f2
となるので
V/f=(Vーvo)/f2
の等式が成り立ち、f2について解いてみると、
f2=(Vーvo)/V・f
となり、観測者が動くときのドップラー効果の式を導くことができました。
音源と観測者の両方が動くとき
それでは最後に、音源と観測者の両方が動くときのドップラー効果の式を導いてみます。
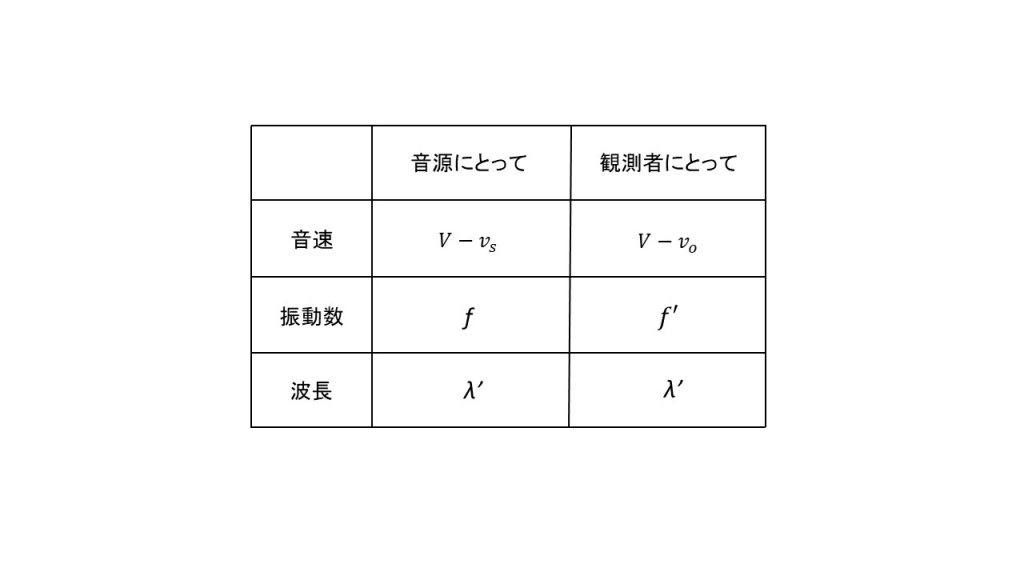
音源にとっての音速は、音源が動いているので相対速度の考え方を使い、Vーvsとなります。
また、音源にとっての振動数はやはり変わらずfのままです。
そして、音源にとっての波長は音源が動いているので変化します。
次に観測者にとってですが、観測者にとっての音速は観測者が動いているので相対速度の考え方を使いVーvoとなります。
また、観測者にとっての振動数は波の波長が変化しており、さらに観測者自身も動いているので当然変化します。
そして、観測者にとっての波長はやはり音源にとっての波長と等しくなります。
よって、音源にとっての波の基本式は
λ’=(Vーvs)/f
となり、観測者にとっての波の基本式は
λ’=(Vーvo)/f’
となるので、
(Vーvs)/f=(Vーvo)/f’
の等式が成り立ち、この等式をf’について解くと、
f’=(Vーvo)/(Vーvs)・f
というドップラー効果の式を導くことができました。
いかがだったでしょうか。ドップラー効果の式はこのように原理を分かったうえで使うようにすると応用させることができます。
また、ドップラー効果の問題で分からなくなった場合は、ベルトコンベアで考えてみるようにしましょう。
(3)解説授業の内容を復習しよう
(4)音波(物理基礎、物理)の解説一覧
③定常波についてのまとめ(定常波とは何か、固定端反射と自由端反射、弦で発生する定常波、気柱で発生する定常波、固有振動とは、音(縦波)の大きさ(密度の変化)が最大になるときについても解説しています)
④ドップラー効果の式を導こう(ベルトコンベアによるドップラー効果のモデルについても解説しています)
(5)参考
☆物理の解説動画・授業動画一覧(力学・熱力学・波動・電磁気・原子)
☆物理に関する現象や技術(力学、熱力学、波動、電磁気、原子)
