(1)解説授業動画
☆YouTubeチャンネルの登録をよろしくお願いします→大学受験の王道チャンネル
(2)解説授業の原稿
チェバの定理とメネラウスの定理の簡単な使い方を紹介します。
チェバの定理の使い方
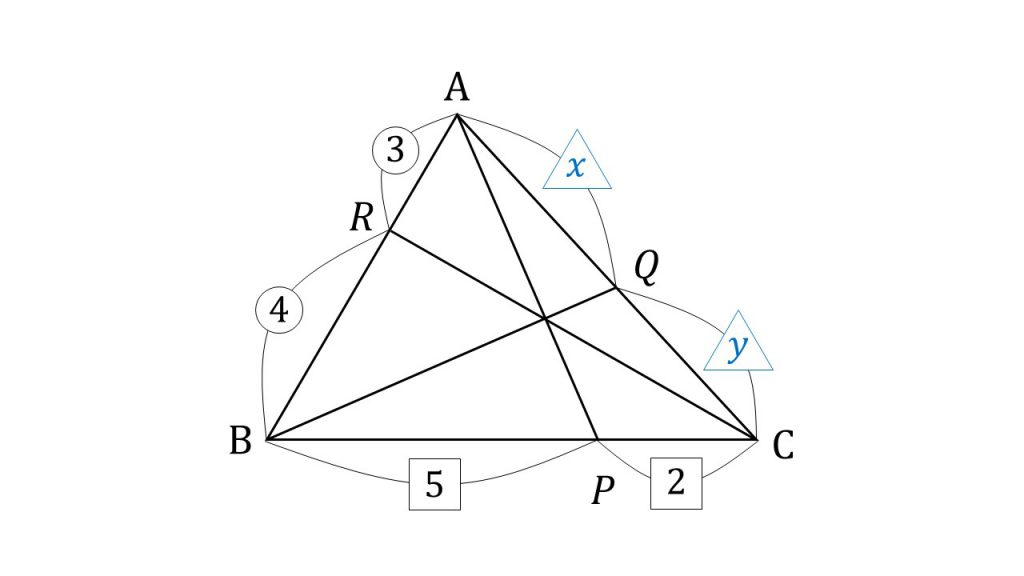
例えば、△ABCがあり、辺BCを5:2で内分する点をP、辺ACをx:yで内分する点をQ、辺ABを3:4で内分する点をRとした場合、AQ:QCの比を求めてみましょう。
三角形の頂点から引かれた線が一点で交わるときはチェバの定理が使えます。チェバの定理を教科書の通りに書くと次のようになります。
BP/PC・CQ/QA・AR/RB=1
しかし、この分数の順番や、どちらが分母になりどちらが分子になるかは必ずしもこの通りでなくてもよいです。
チェバの定理を使うときのキーワードは
「2ステップ3ターンで帰ってくる」
です。これでチェバの定理を使うようにすると簡単に使えます。
「2ステップ3ターンで帰ってくる」を使う
チェバの定理が使える状況で「2ステップ3ターンで帰ってくる」を使うために、まずスタートとなる頂点を1つ決めます。たとえば頂点Aをスタートとすると、
RB/AR・PC/BP・QA/CQ=1
となります。この式に内分の比を代入すると、次のようになります。
4/3・2/5・x/y=1
これを解くと、x:y=15:8となります。
このように、「2ステップを3ターン行い、元の頂点に帰ってくる」というイメージで式を作ることができます。
「2ステップ3ターンで帰ってくる」の様々な式の立て方
他のパターンとして、分子と分母を逆にしても問題ありません。
3/4・5/2・y/x=1
また、スタートとなる頂点を別の頂点にしてもできます。以下はCをスタートとした場合です。
x/y・4/3・2/5=1
このように、ちゃんと2ステップ3ターンで帰ってくれば、様々な式の立て方ができます。
メネラウスの定理の使い方
また、メネラウスの定理でも、「2ステップ3ターンで帰ってくる」のやり方が使えます。
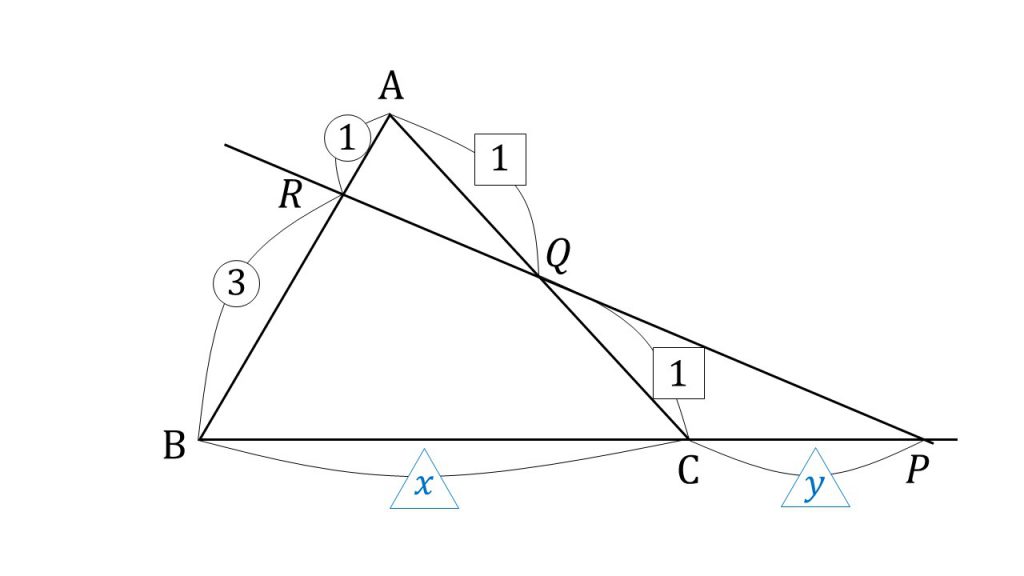
△ABCに直線が交わっており、BCと直線の交点をP、ACと直線の交点をQ、ABと直線の交点をRとし、BP:PC=x+y:y、AQ:QC=1:1、AR:RB=1:3とします。
このように三角形と直線がある場合は、メネラウスの定理を考えます。メネラウスの定理は、教科書には次のように書いてあります。
RB/AR・PC/BP・QA/CQ=1
しかし、こちらも必ずしもこの通りに式を立てる必要はありません。
「2ステップ3ターンで帰ってくる」を使う
チェバの定理のときと同様に、まずはスタートとなる頂点を決めます。そして2ステップ3ターンで最初の頂点に帰ってきます。以下はスタートを頂点Aとしたときです。
RB/AR・PC/BP・QA/CQ=1
となります。つまり、
3/1・y/(x+y)・1/1=1
となるので、これを計算して、x:y=2:1と求められます。
「2ステップ3ターンで帰ってくる」の様々な式の立て方
この他にもスタートは頂点A, B, Cのどこでもいいので、例えば頂点Cをスタートとして
(x+y)/y・1/3・1/1=1
としたり、あるいは進む向きを逆にして
1/1・3/1・y/(x+y)=1
としたりしても問題ありません。
このように、チェバの定理やメネラウスの定理は「2ステップ3ターンで帰ってくる」というキーワードで使うようにすると簡単に式を立てることができます。
(3)解説授業の内容を復習しよう
①図形(数学A)問題演習(2015年センター試験本試験数学ⅠA第6問)
②図形(数学A)問題演習(2016年センター試験本試験数学ⅠA第5問(1))
