(1)例題
図のように、電圧Vの直流電流、抵抗値Rの抵抗、電気容量Cのコンデンサーおよびスイッチを接続した。はじめスイッチは開いており、コンデンサーに電荷は蓄えられていない。ただし、図中の矢印の向きを電流𝐼の正の向きとする。
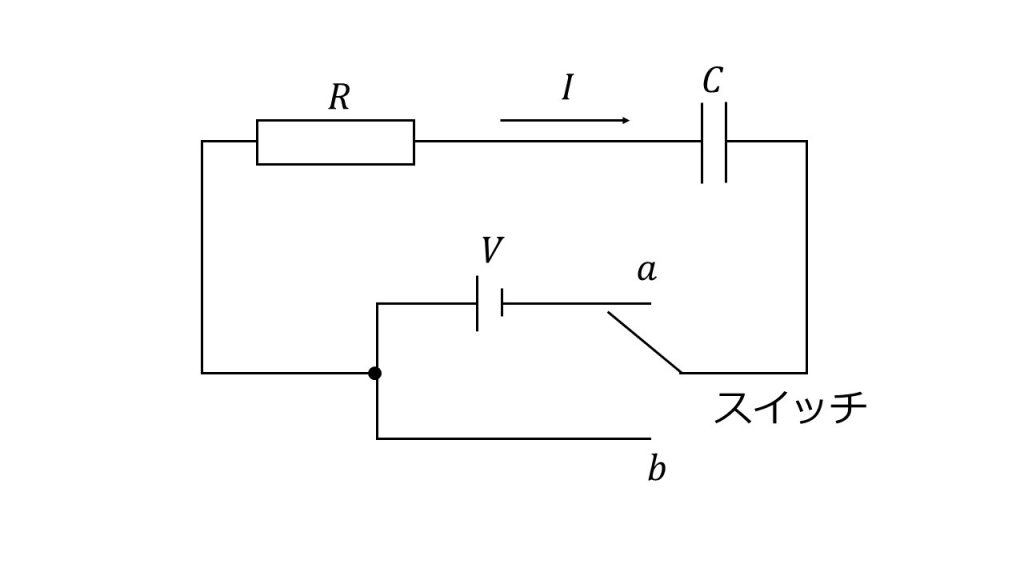
①時刻t=0にスイッチをa側に入れた。コンデンサーに蓄えられた電荷を𝑞、回路に流れる電流を𝐼としたとき、𝐼をqを用いて表せ。また、電流𝐼と時刻tの関係を表すグラフを簡単にかけ。
②スイッチをa側に入れてから十分に長い時間が経過した後、スイッチをb側に入れた。スイッチをb側に入れてから電流が流れなくなるまでの間に、抵抗で発生するジュール熱を表せ。
(2018年センター試験本試物理第2問A)
③下図のように、電気容量がそれぞれ4µF, 3µF, 1µFのコンデンサーC1, C2, C3をつなぎ、端子a, bに10Vの直流電流をつないだ。このとき、コンデンサーC1, C2, C3にそれぞれ蓄えられる電気量Q1, Q2, Q3を求めよ。
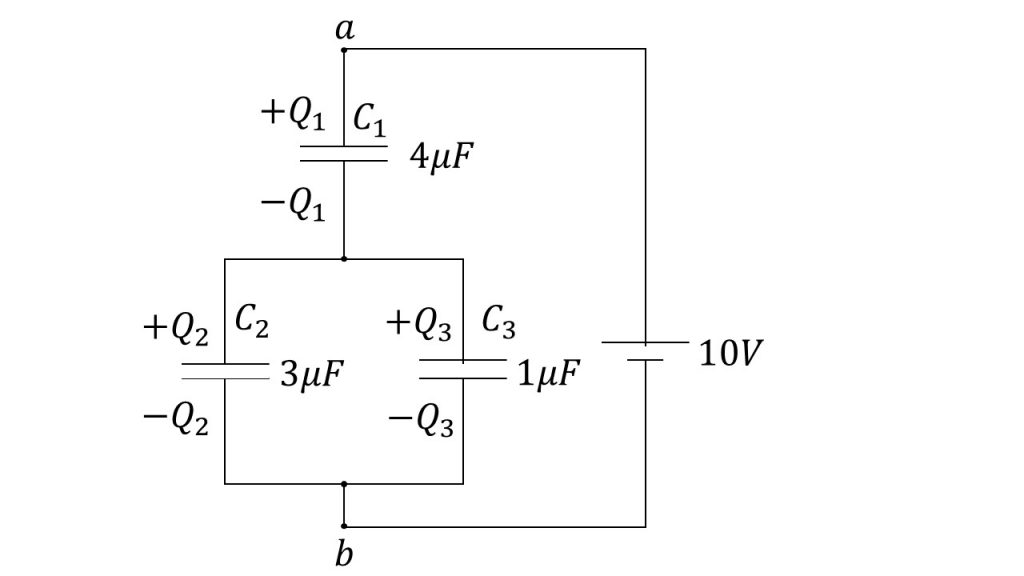
(2016年センター試験本試物理第2問改A問1改)
(2)例題の答案
①



②

③電気量保存則より
0=-Q1+Q2+Q3
∴ Q1=Q2+Q3 ・・・(ア)
また、コンデンサーC1, C2, C3にかかる電圧をそれぞれV1, V2, V3とすると、コンデンサーの基本式より
Q1=4×10-6×V1 ・・・(イ)
Q2=3×10-6×V2 ・・・(ウ)
Q3=1×10-6×V3 ・・・(エ)
さらに、キルヒホッフの第二法則より
10=V1+V2 ・・・(オ)
10=V1+V3 ・・・(カ)
(イ)(ウ)(オ)より
3Q1+4Q2=12×10-5 ・・・(キ)
(イ)(エ)(カ)より
Q1+4Q3=4×10-5 ・・・(ク)
(キ)+(ク)より
4Q1+4Q2+4Q3=16×10-5 ・・・(ケ)
(ア)×4+(ケ)より
8Q1=16×10-5
∴ Q1=2×10-5〔C〕
(キ)(ク)より
Q2=1.5×10-5〔C〕
Q3=5×10-6〔C〕
③別解(コンデンサーの合成を使った答案)
コンデンサーC2とC3を合成してできるコンデンサーの電気容量をC23とすると
C23=C2+C3=4×10-6〔F〕
コンデンサーC1, C2にかかる電圧をそれぞれV1, V2とすると、コンデンサーC2とC3は並列なのでコンデンサーC3, C23にかかる電圧もV2となる。
コンデンサーC1とC2は直列なので、V1とV2の比はC1とC23の逆数の比となる。
よって
V:V1:V2=1/C1+1/C23:1/C1:1/C23
であるので
V1=V2=5〔V〕
したがって、
Q1=C1×V1=2×10-5〔C〕
Q2=C2×V2=1.5×10-5〔C〕
Q3=C3×V2=5×10-6〔C〕
(3)解法のポイント
①③コンデンサーを含む回路は、
ⅰ)コンデンサーの基本式
ⅱ)電気量保存則
ⅱ)キルヒホッフの第1法則
ⅲ)キルヒホッフの第2法則
この4つを使って、必要な数だけ式を作るのが基本方針です。③は未知数がQ1, Q2, Q3, V1, V2, V3の6個となるので、式が6個必要になります。
②回路でもエネルギーの保存則が成り立ちます。つまり、電源につながれていないのであれば、ジュール熱を生み出しているのは、コンデンサーに蓄えられていた静電エネルギーしかないということになります。
(4)必要な知識
①基本式

②キルヒホッフの法則

③静電エネルギー

④コンデンサーの合成

(5)理解すべきこと
①回路は水路をイメージすると理解しやすくなります(キルヒホッフの第1法則、キルヒホッフ第2法則、抵抗の合成についても解説しています)
