(1)例題
9人を次のように分ける方法は何通りあるか。
①4人、3人、2人の3組に分ける。
②3人ずつ、A, B, Cの3組に分ける。
③3人ずつ3組に分ける。
④5人、2人、2人の3組に分ける。
(2)例題の答案
①9人のうちから4人を選び、残りの5人から3人を選び、残りの2人から2人を選ぶので
9C4×5C3×2C2=1260通り
②Aに入る3人を選び、残りの6人からBに入る3人を選び、残りの3人からCに入る3人を選ぶので
9C3×6C3×3C3=1680通り
③まずは、組にA, B, Cと名前を付けて組分けをし、その区別をなくせばよいので、
9C3×6C3×3C3÷3!=280通り
④まずは、組にA, B, Cと名前を付けて組分けをし、2人が入っている2組の区別をなくせばよいので、
9C5×4C2×2C2÷2!=378通り
(3)解法のポイント
グループやクラスに分ける問題。グループやクラスに名前がついているときと、ついていないときがあり、それぞれで考え方が違います。
グループやクラスに名前がついている(区別できる)ときは、Cを使って順番に分けていけばよいです。また、人数で区別できるときも同様です(3人、4人、5人に分けるといったように)
しかし、グループやクラスに名前がついておらず、人数でも区別できないとき(3人、3人、3人に分けるといったようなとき)は、割り算をしないといけません。
つまり、まずはグループが区別できるとして並べた後、
(区別できないグループ数)!
で割り算をします。
(4)必要な知識
①Cの定義
→n個のうちからr個選ぶときの選び方
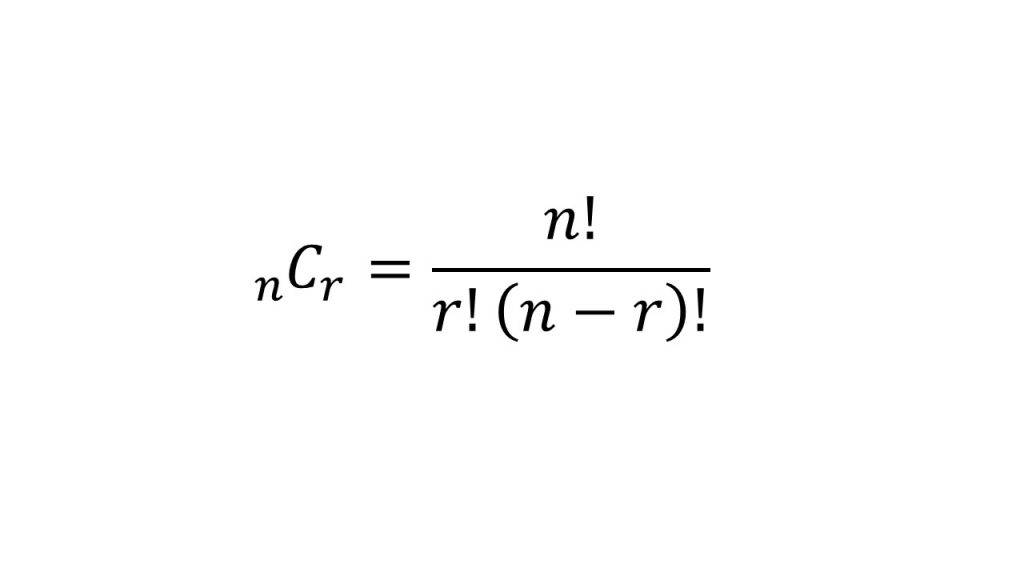
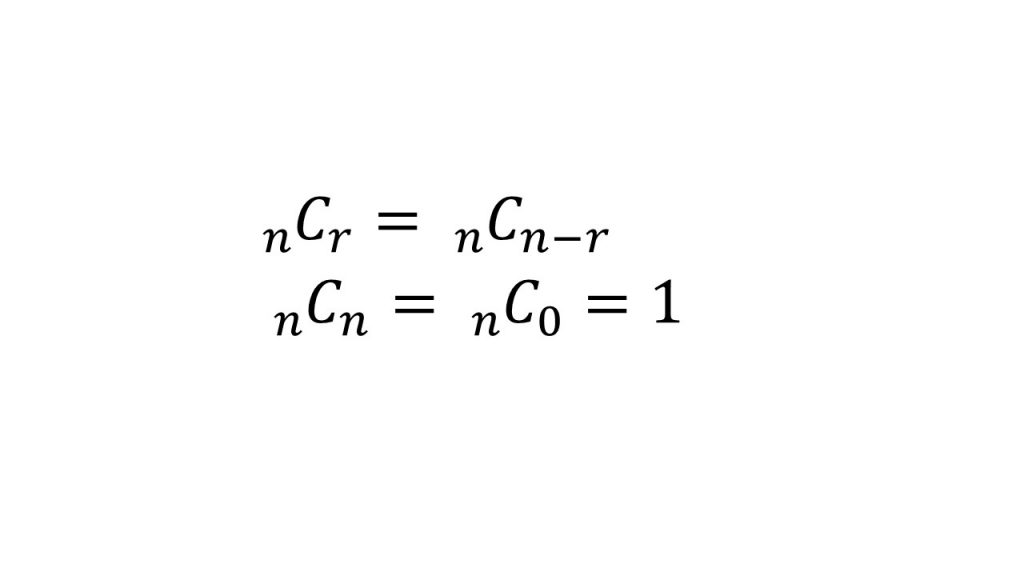
(5)理解すべきこと
組分けの原理を理解しましょう→組分けの原理(なぜ組の数の階乗で割り算をするのか)
☆動画はこちら↓
