☆問題のみはこちら→微分法(数学Ⅲ)の計算公式を証明しよう(問題)
☆公式一覧はこちら→微分法(数学Ⅲ)の計算公式一覧
以下の微分の計算公式を、証明してみましょう!
①xαの微分
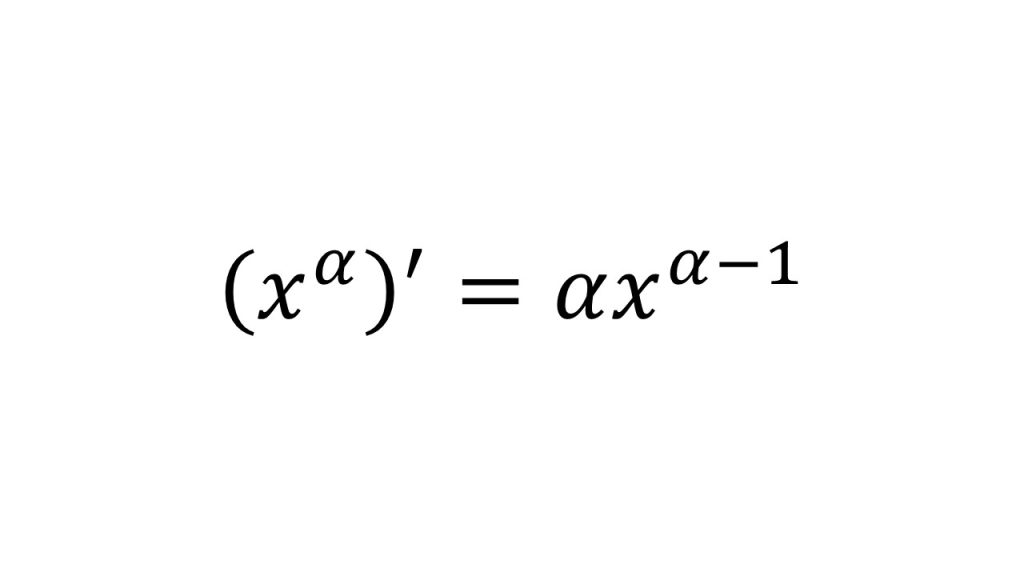
ⅰ)αが自然数のとき(導関数の定義を使って証明する)
【証明】
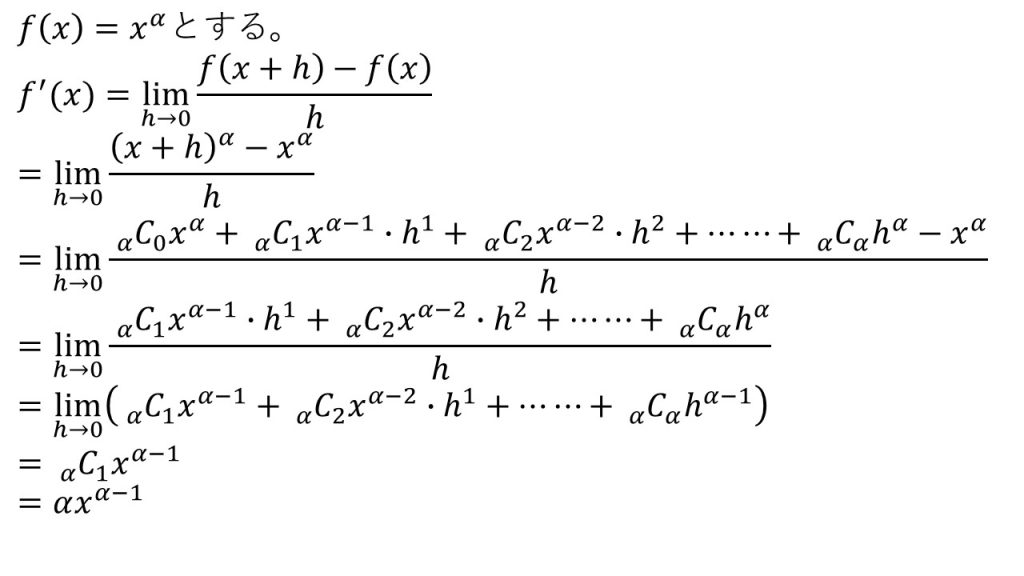
ⅱ)αが実数のとき(対数微分法を使って証明する)
【証明】

- αが自然数でないときは二項定理を使って(x+h)αを展開することができない。そのため、導関数の定義を使って証明することができない。
- 対数微分法を使って証明する。xが正になるか決まらないので、絶対値をつけるのを忘れないようにする。
②積の微分
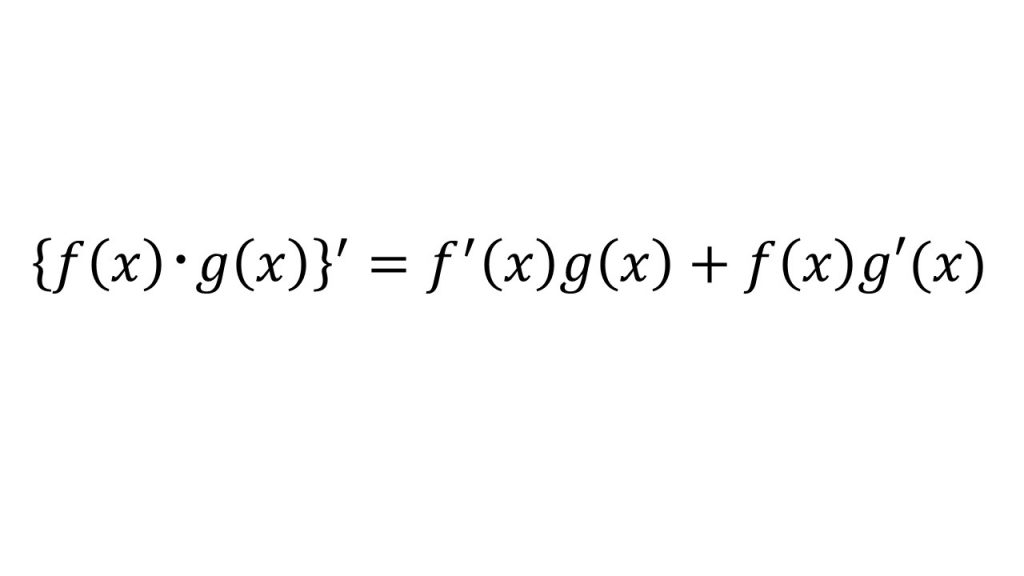
【証明】
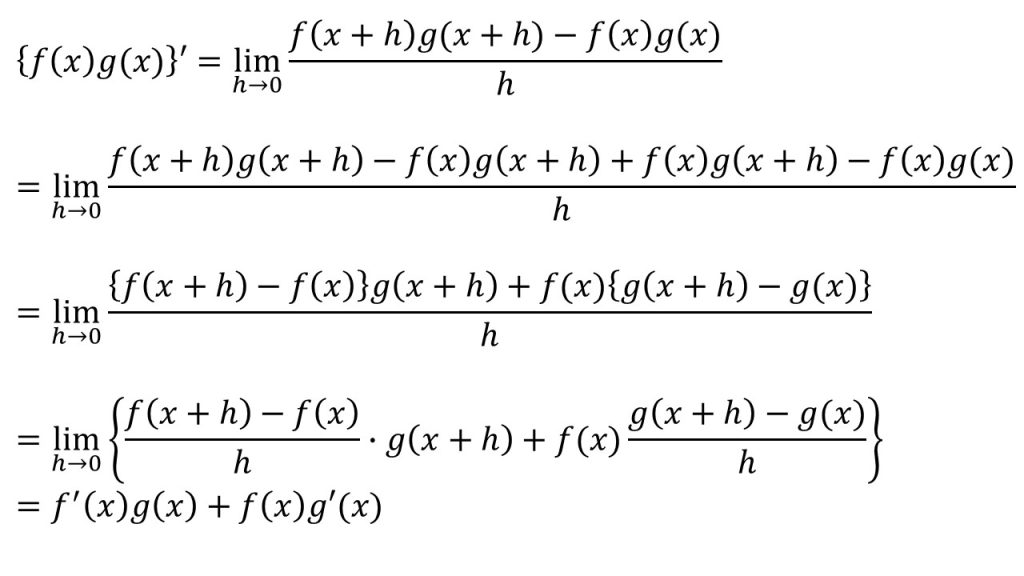
- 導関数の定義を使って証明する。
- f(x+h)-f(x)とg(x+h)-g(x)の形を分子に作るために、-f(x)g(x+h)+f(x)g(x+h)を加えることがポイント。
③商の微分1
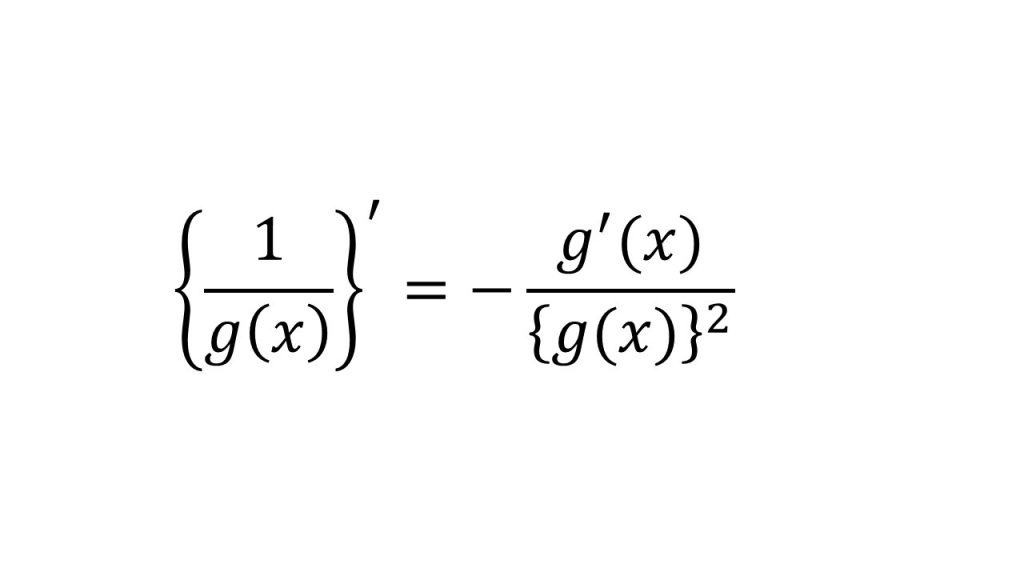
【証明】

- 導関数の定義を使って証明する。
- g(x+h)-g(x)の形を分子に作ることがポイント。
④商の微分2
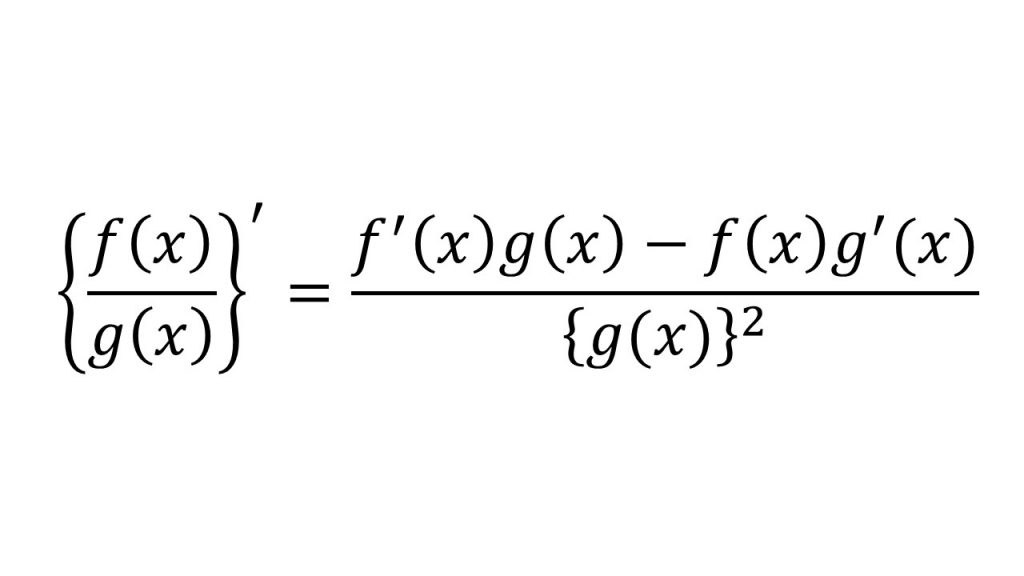
【証明】
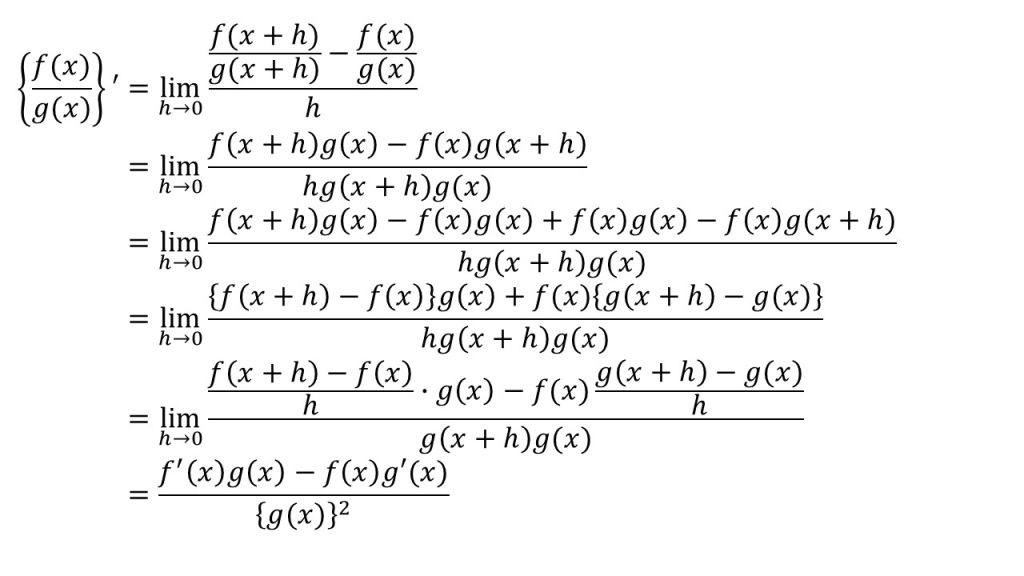
- 導関数の定義を使って証明する。
- f(x+h)-f(x)とg(x+h)-g(x)の形を分子に作るために、-f(x)g(x)+f(x)g(x)を加えることがポイント。
⑤sinxの微分
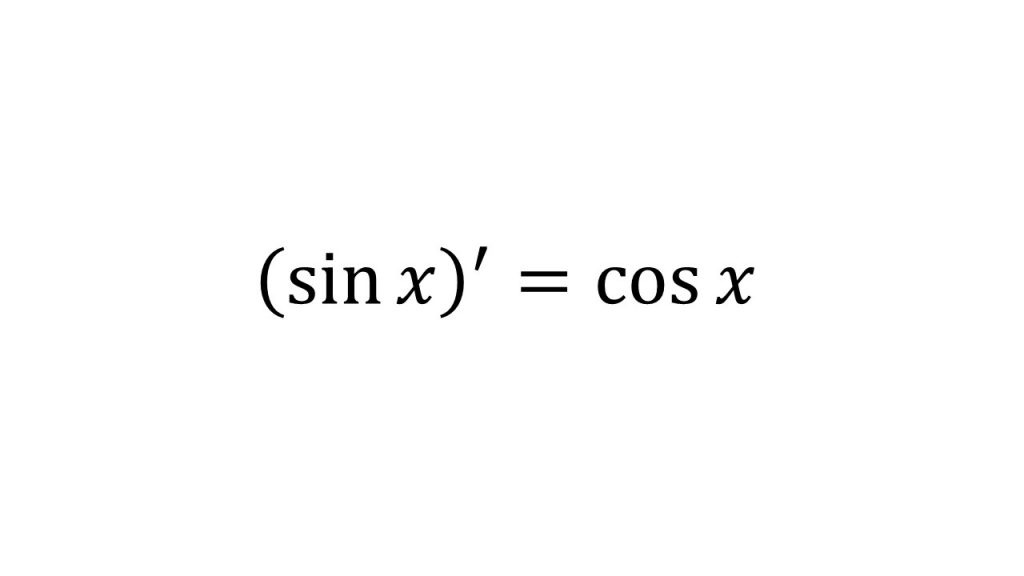
【証明】
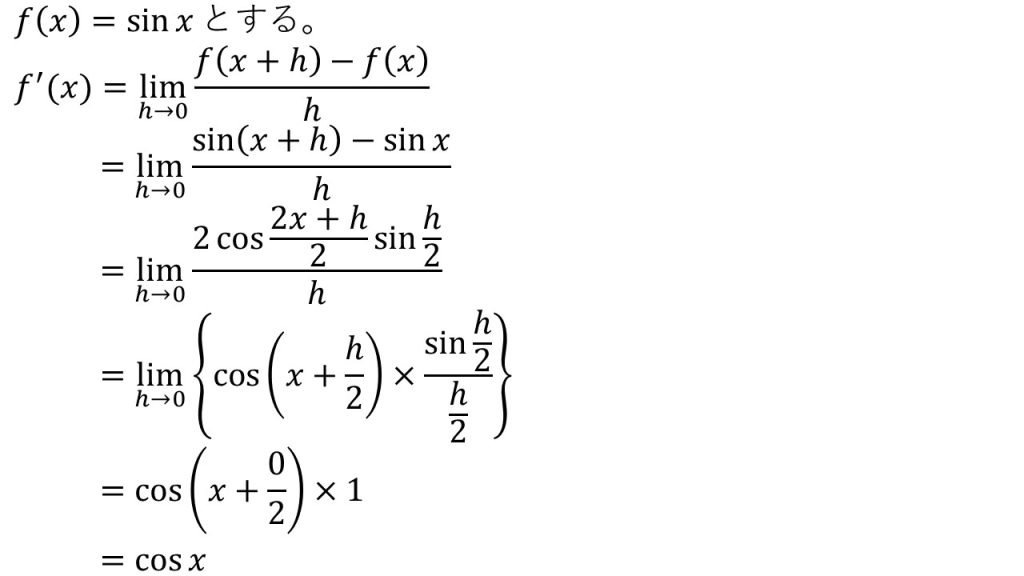
- 導関数の定義を使って証明する。
- 和積の公式を使って式変形をしている。
- sin〇/〇の極限を考えるときは、〇の部分が同じものになるように式変形をする。
- 加法定理を利用して式変形することもできるが、計算が面倒になる。
⑥cosxの微分
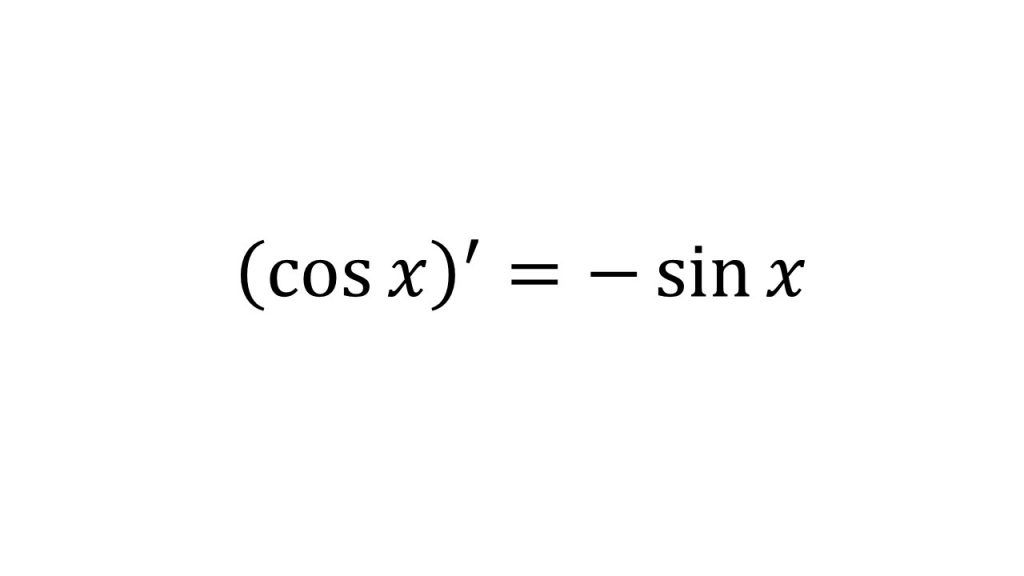
【証明】
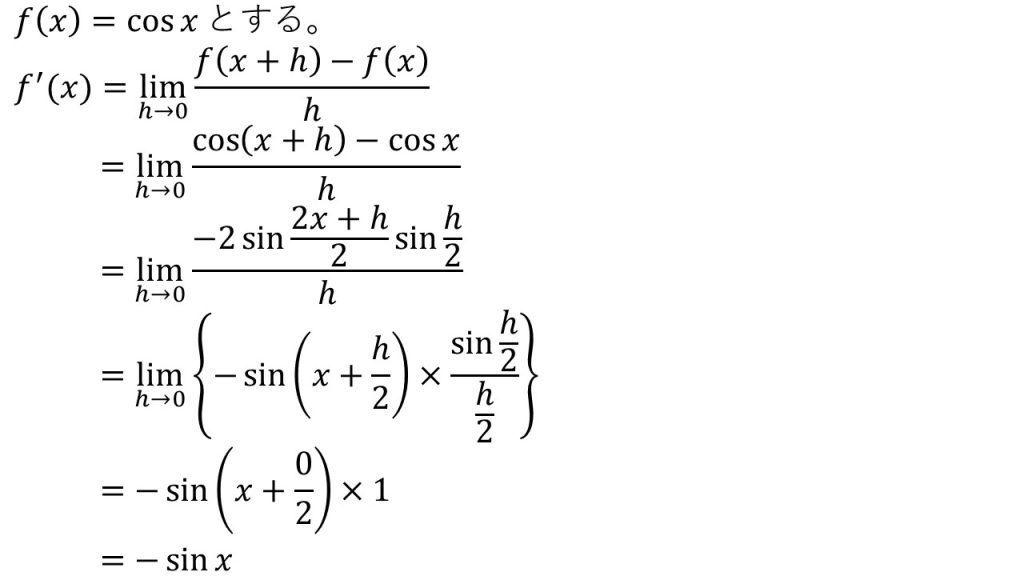
- 導関数の定義を使って証明する。
- 和積の公式を使って式変形をしている。
- sin〇/〇の極限を考えるときは、〇の部分が同じものになるように式変形をする。
- 加法定理を利用して式変形することもできるが、計算が面倒になる。
⑦tanxの微分
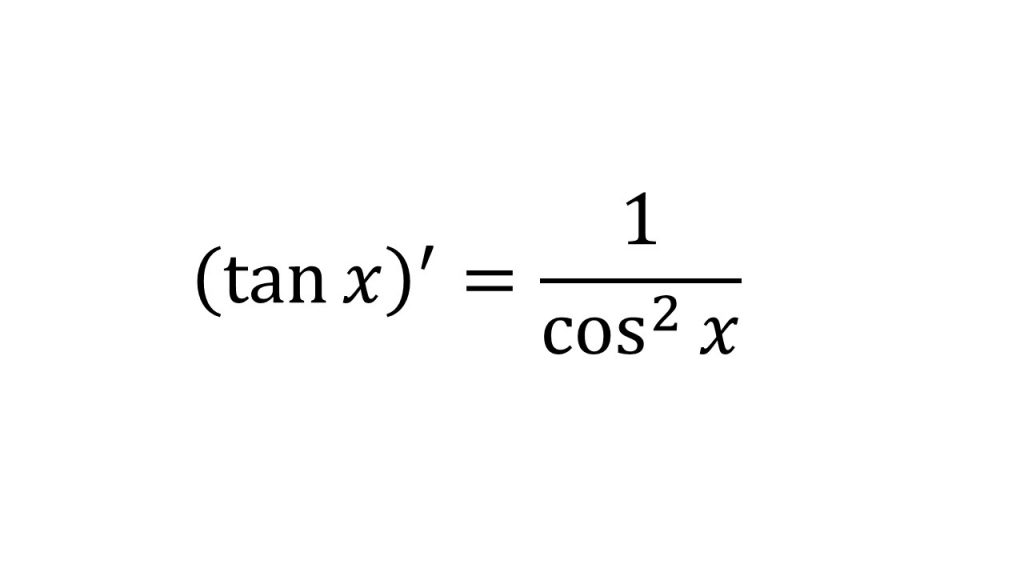
【証明】
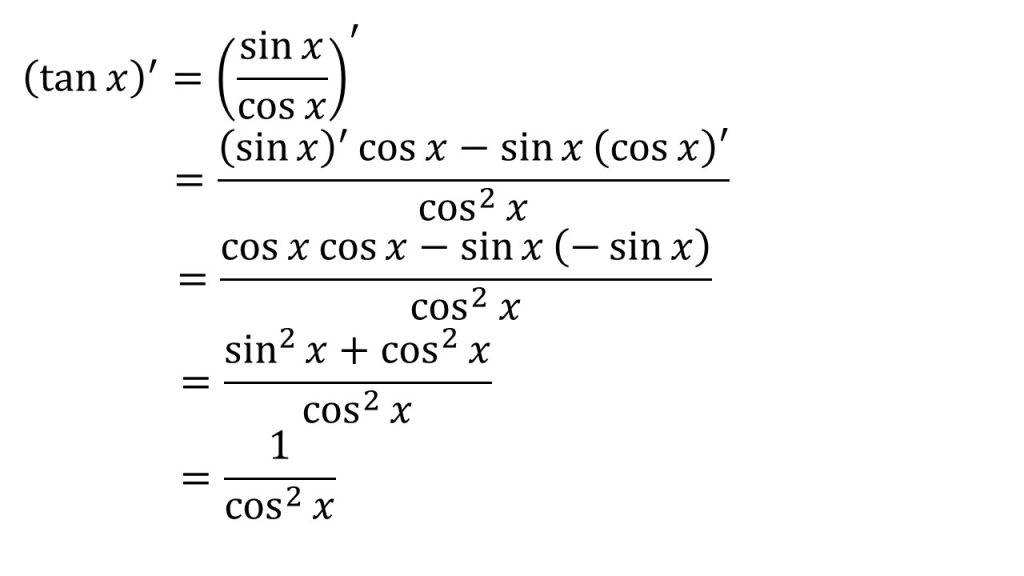
- 商の微分を利用する。
⑧exの微分
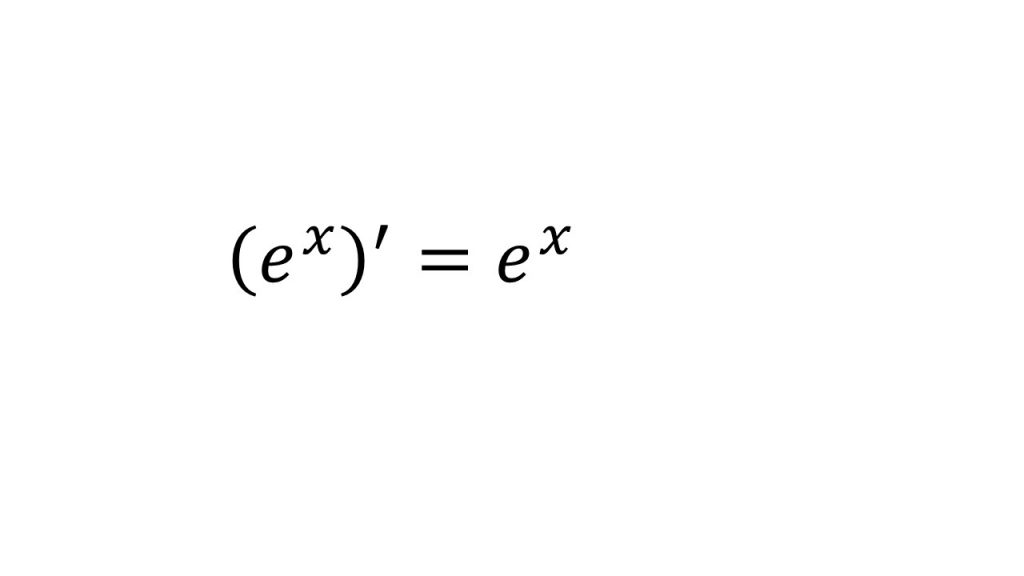
【証明】

- 導関数の定義を使って証明する。
- 自然対数eを使った極限の公式は理解しておこう。
⑨axの微分(a>0, a≠1)
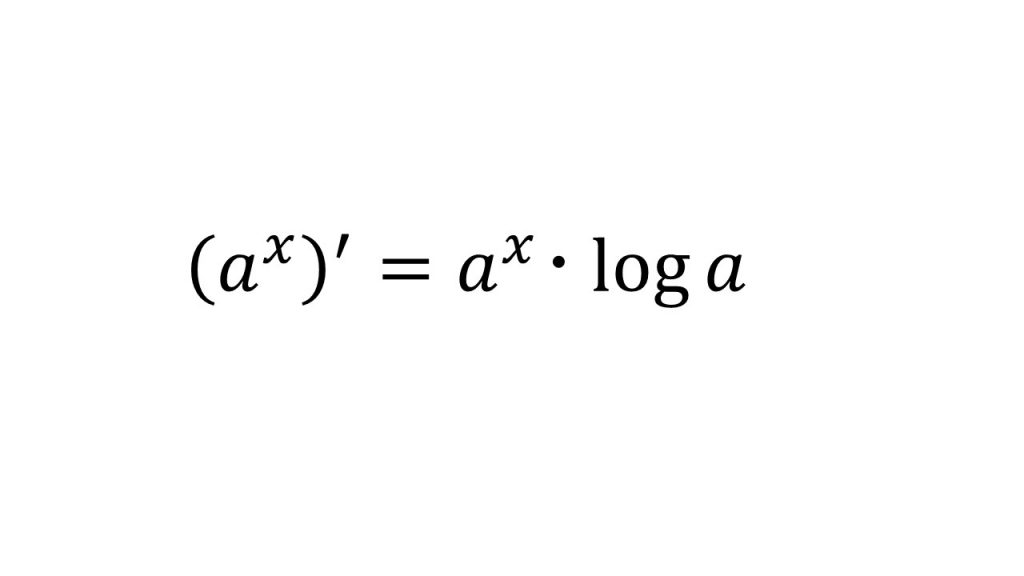
【証明】

⑩対数関数の微分(底がeのとき)

【証明】
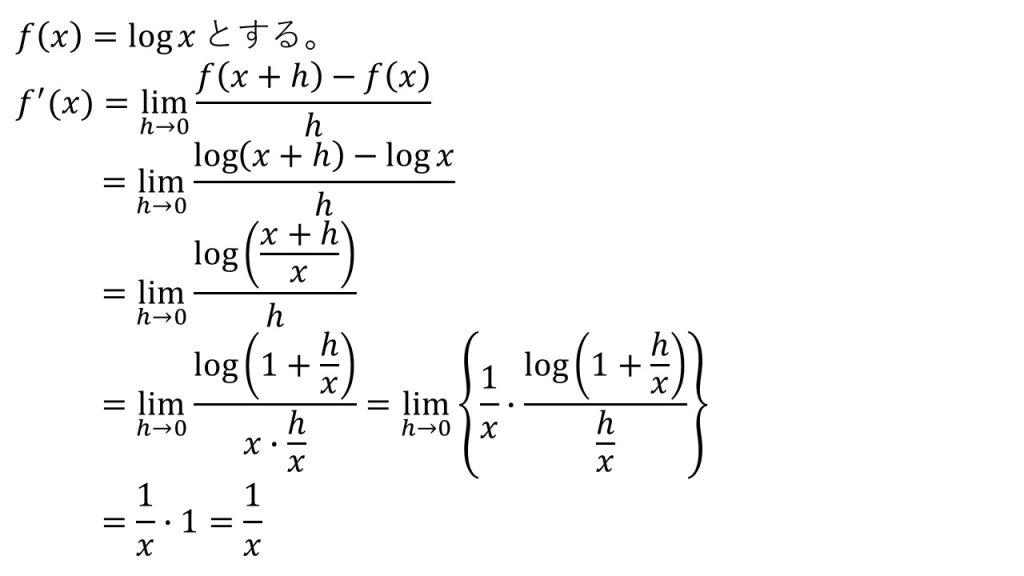
- 導関数の定義を使って証明する。
- 自然対数eを使った極限の公式は理解しておこう。
⑪対数関数の微分(底がeではないとき)
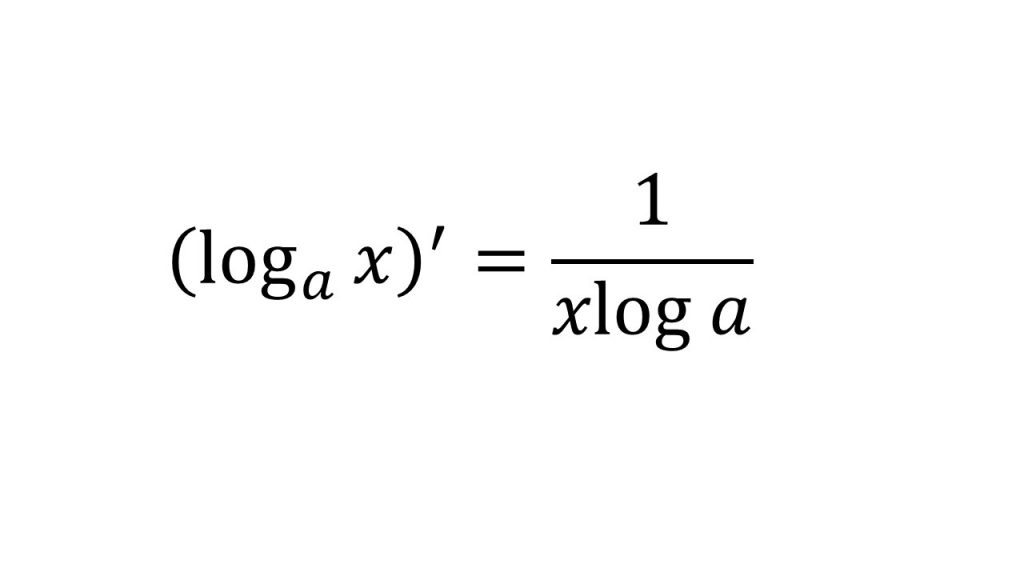
【証明】

- 導関数の定義を使って証明する。
- 自然対数eを使った極限の公式は理解しておこう。
⑫対数関数の微分2(底がeのとき)
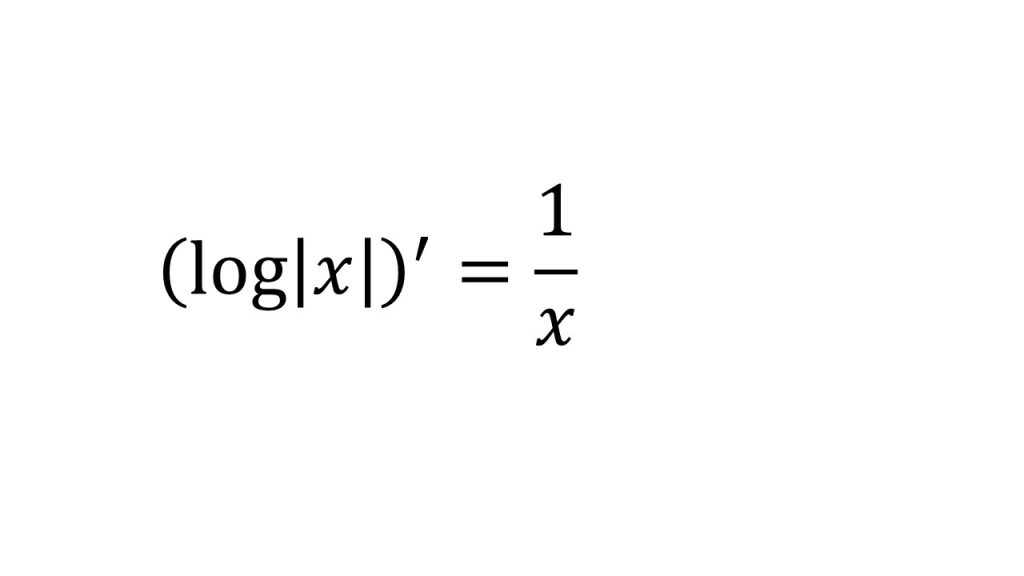
【証明】

- 絶対値を処理するために場合分けをする。
- log(-x)の微分は合成関数の微分
⑬対数関数の微分2(底がeではないとき)
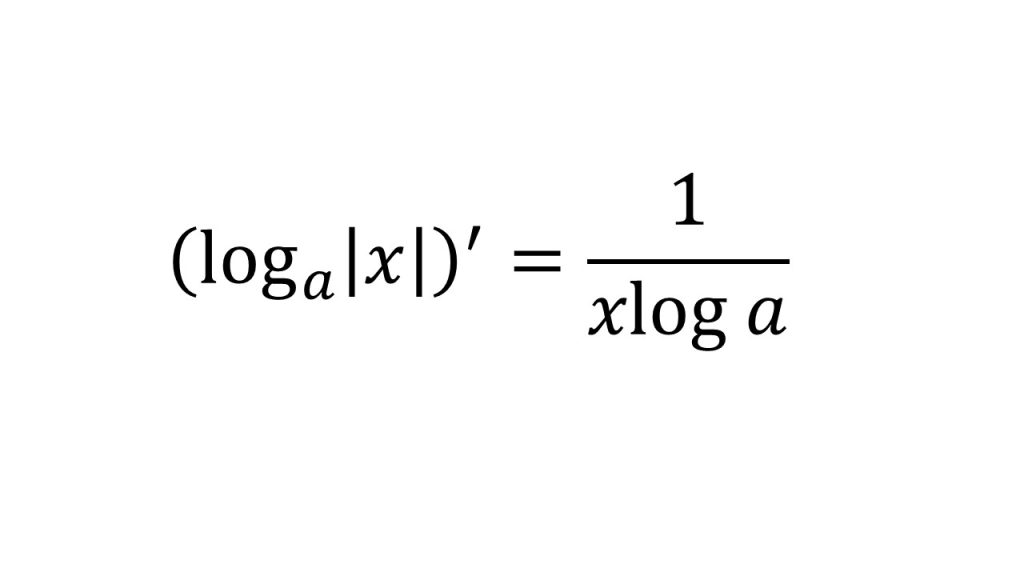
【証明】
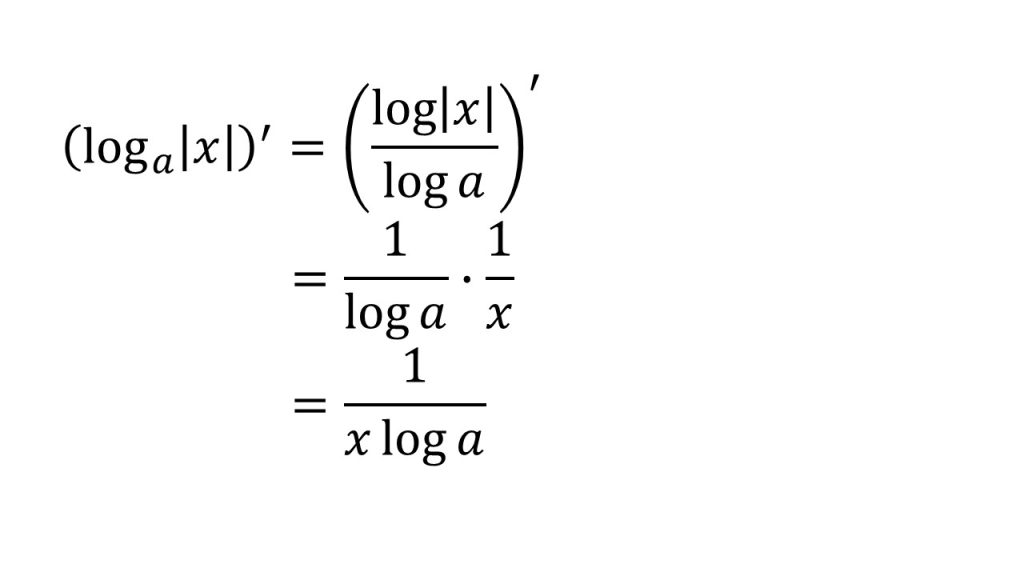
- 底の変換公式を用いる。
☆問題のみはこちら→微分法(数学Ⅲ)の計算公式を証明しよう(問題)
☆公式一覧はこちら→微分法(数学Ⅲ)の計算公式一覧
【微分計算(数学Ⅲ)の演習問題一覧】
☆微分の計算公式の証明はこちら→微分(数学Ⅲ)の計算公式を証明しよう
~参考~
☆微分計算(数学Ⅲ)をマスターしよう(解説・授業・公式・演習問題一覧)
