(1)例題

(2016年センター試験本試数学ⅡB第4問(1)より)
(2)例題の答案
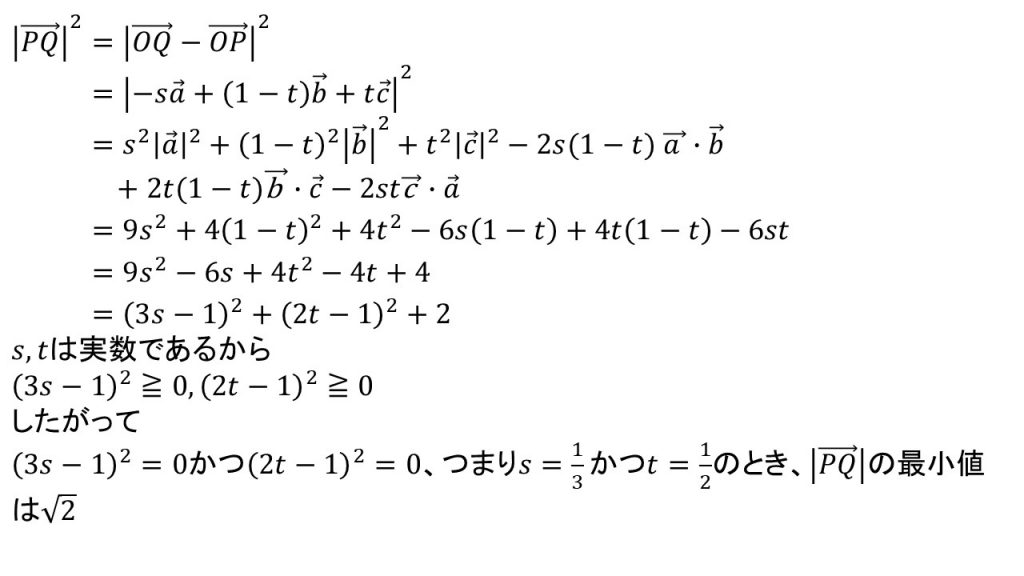
(3)解法のポイント
ベクトルの大きさの最小値を求める問題は、ベクトルで重要な解法の1つである、
「大きさは2乗する」
を使います。
大きさを2乗すると、おそらく2次関数となるので、2次関数の最小を求める問題となります。
大きさは0以上であるから、大きさの2乗の最小値は大きさの最小値となります。この「大きさは0以上である」の断り書きは必要です(もしなければ減点される可能性があります)
※参考:二次関数の最大・最小(基本)
二次関数の最大・最小を求めるときに、縦に引くべき3つの線である
①範囲
②範囲の真ん中
③軸
は必ず引くようにしましょう。
(4)必要な知識
①始点をそろえる

(5)理解すべきこと
こちらのコアを理解しましょう→ベクトルの問題で重要な解法
動画はこちらです↓
