(1)例題
①y=x2−2ax+3の0≦x≦4における最小値を求めよ。
②y=−2x2+6x+3のa≦x≦a+1における最小値を求めよ。
(2)例題の答案
①
y=x2−2ax+3=(x−a)2−a2+3
軸は、x=a
ⅰ)a<0のとき
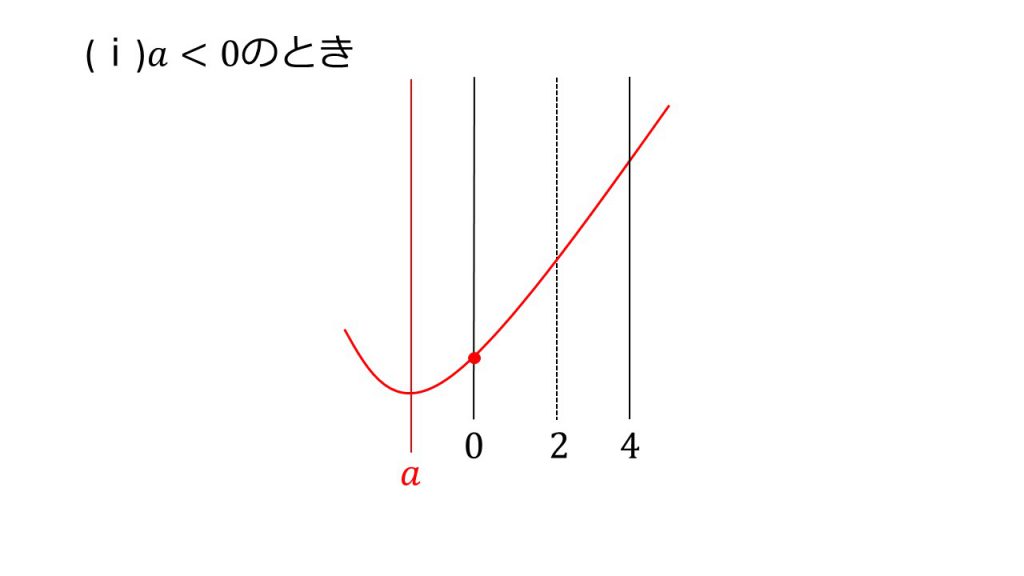
x=0のとき最小値 3
ⅱ)0≦a≦4のとき
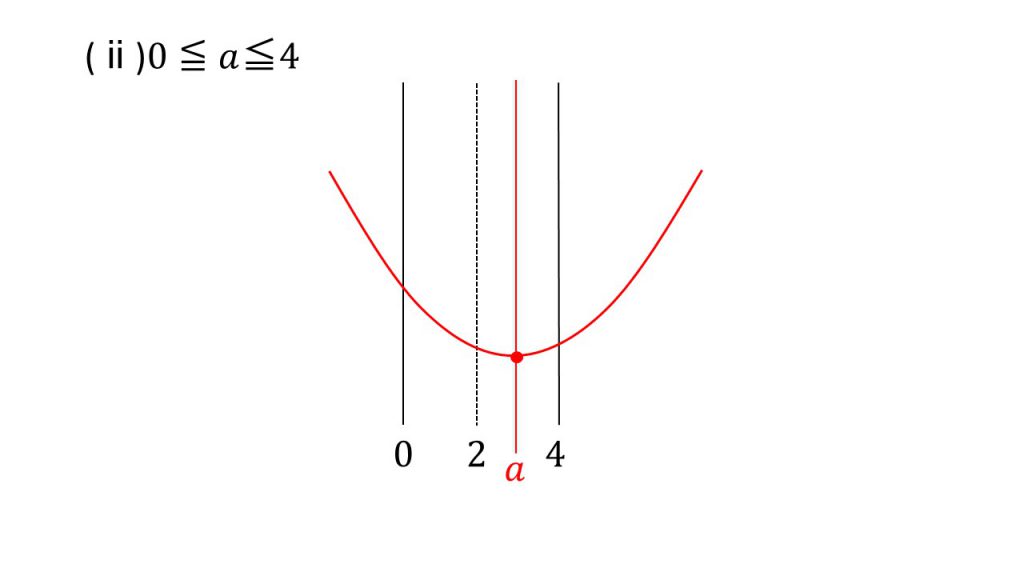
x=aのとき最小値 −a2+3
ⅲ)4<aのとき
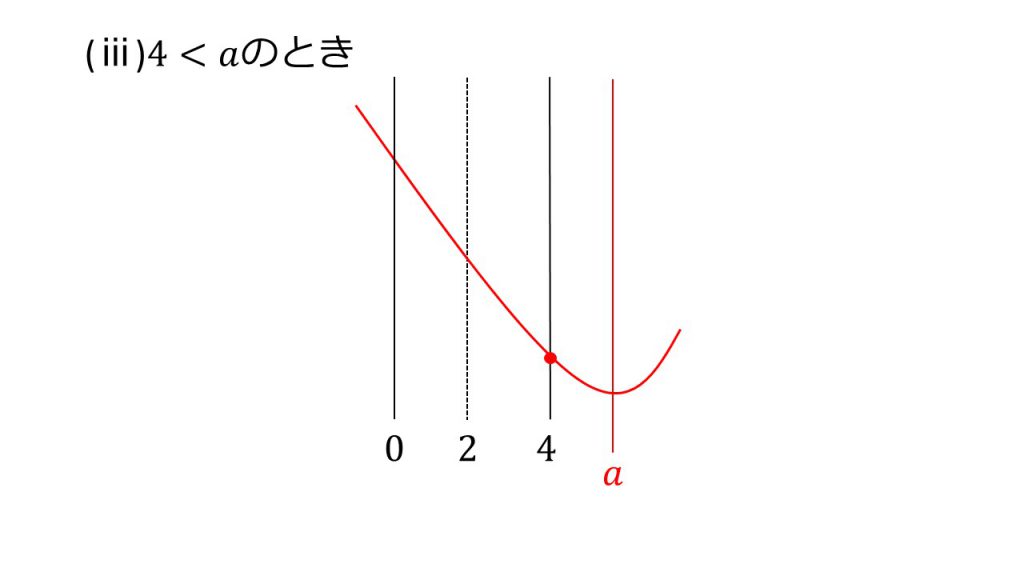
x=4のとき最小値 −8a+19
②
y=−2x2+6x+3=−2(x−3/2)2+15/2
軸は、x=3/2
ⅰ)3/2<a+1/2 つまり 1<aのとき
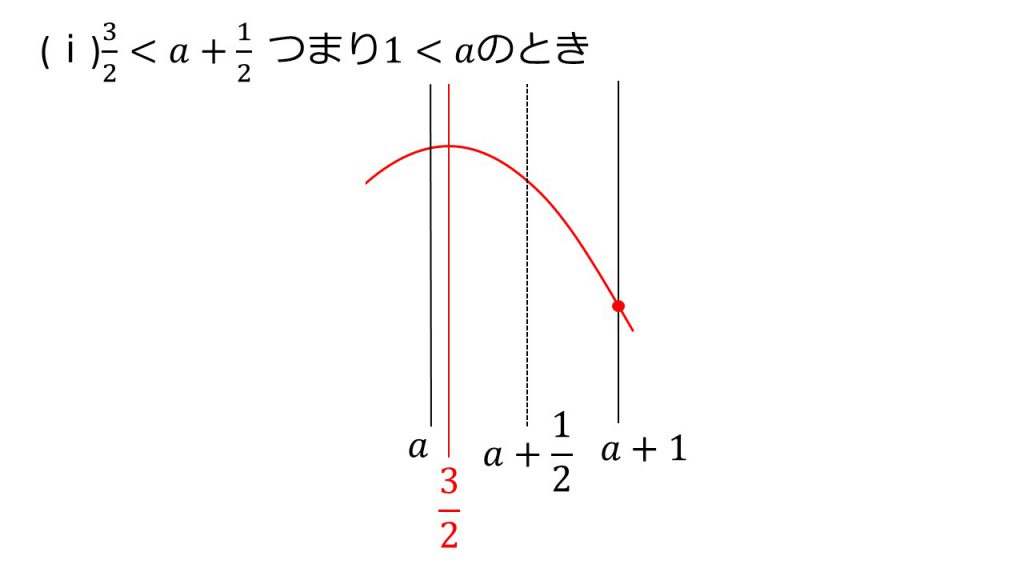
x=a+1のとき最小値 −2a2+2a+7
ⅱ)a+1/2=3/2 つまり a=1のとき

x=1またはx=2のとき最小値 7
ⅲ)a+1/2<3/2 つまり a<1のとき
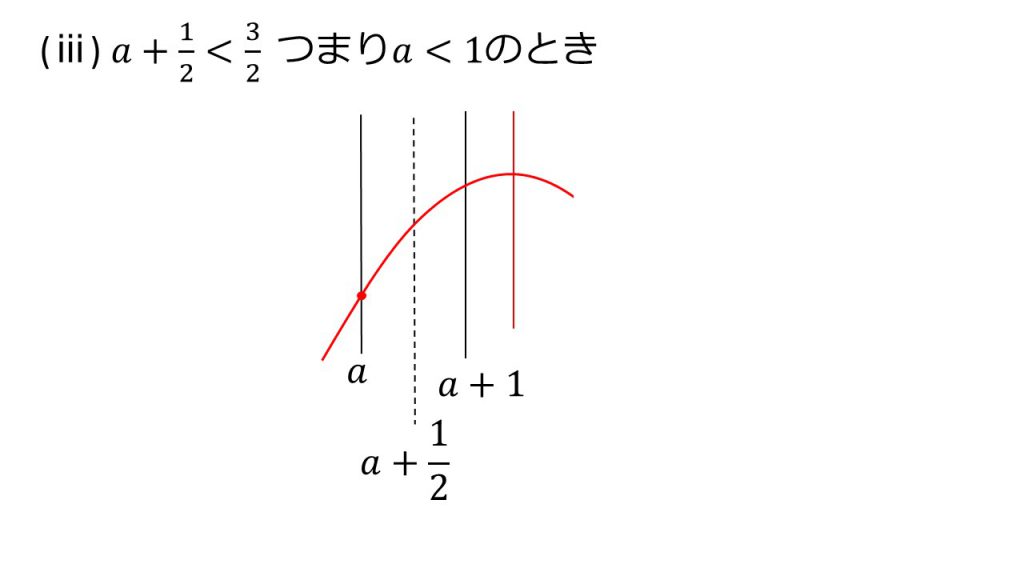
x=aのとき最小値 −2a2+6a+3
(3)解法のポイント
軸や範囲に文字が含まれている場合の二次関数の最大・最小を求める問題は場合分けが必要となります。
場合分けを考えるためにも、まず二次関数の最大・最小を求めるときの基本を確認します。二次関数の最大・最小を求める問題を解くときは、縦に3つの線を引きます。
①定義域
②定義域の中央
③軸
この3つです(範囲は両端があるので、線の本数は4本になることが多い)これが基本で、必ずこのやり方でやらないといけません。
しかし、範囲や軸に文字が含まれているときは、これらの位置関係が確定しないので、場合分けが必要になります。
すなわち、以下の4つの場合分けのパターンがあります。
①下に凸で最小値
ⅰ)軸が範囲の左、ⅱ)軸が範囲の中、ⅲ)軸が範囲の右
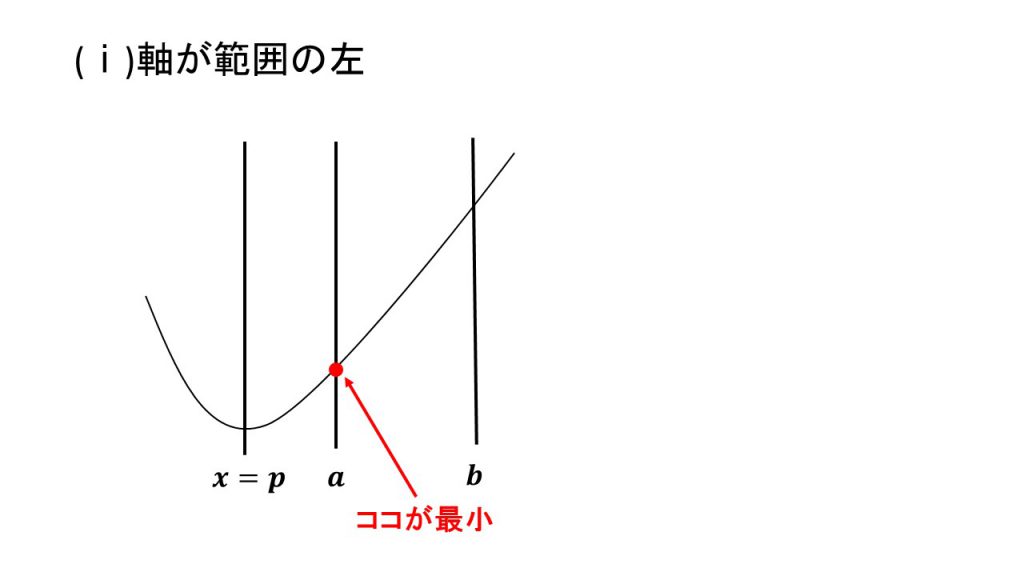
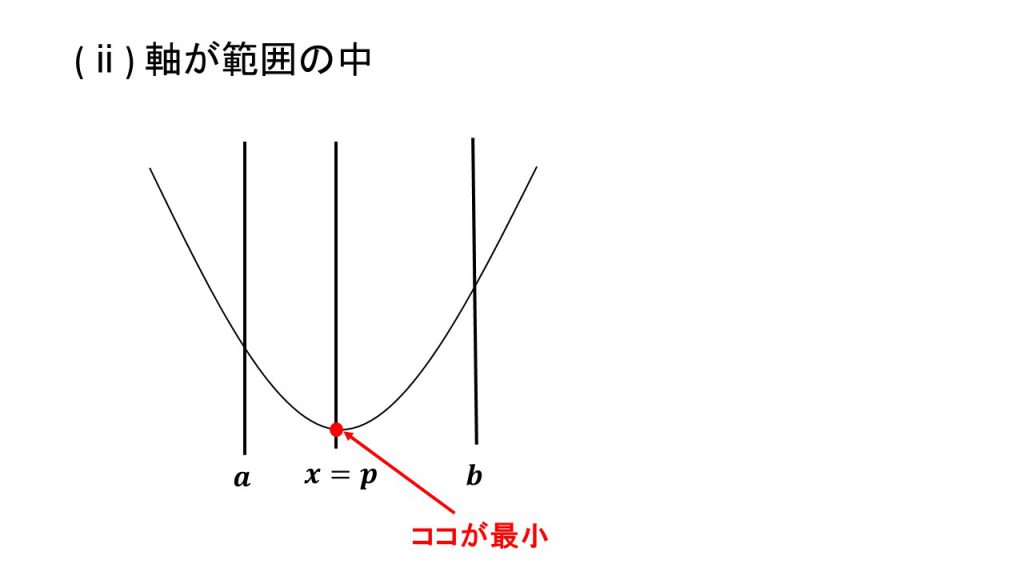

②下に凸で最大値
ⅰ)軸が範囲の真ん中より左、ⅱ)軸が範囲の真ん中と一致、ⅲ)軸が範囲の真ん中より右
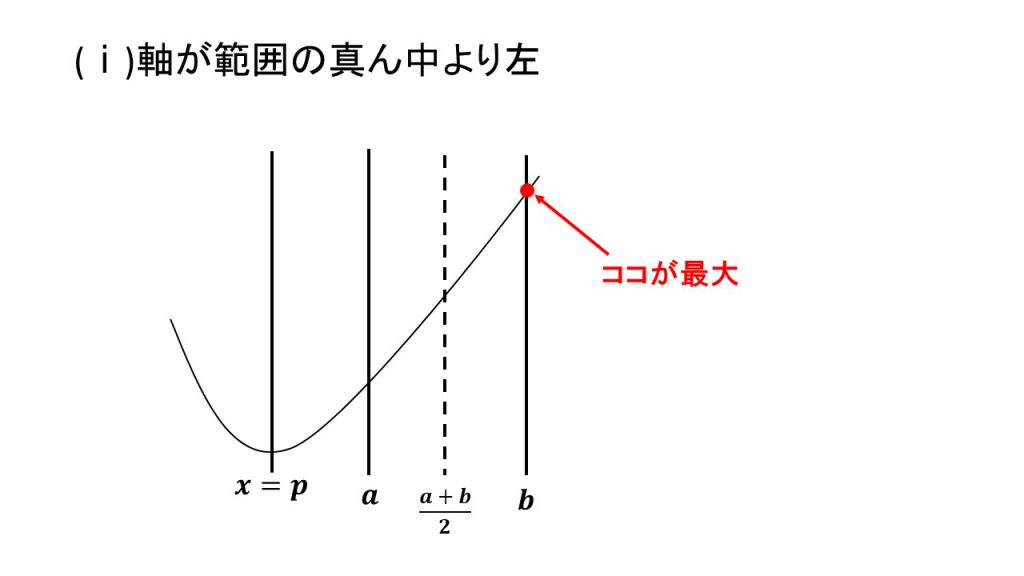

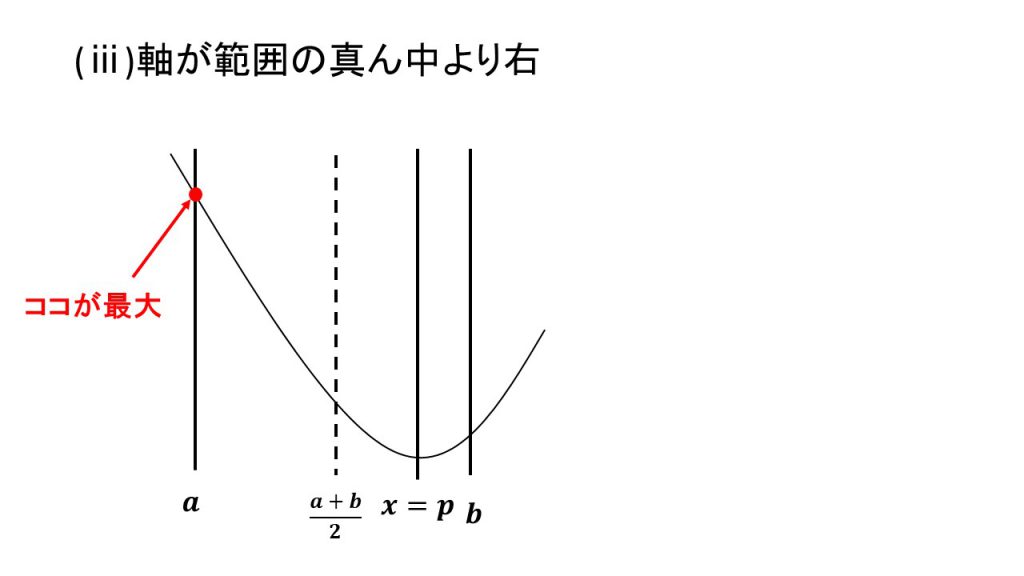
③上に凸で最小値
ⅰ)軸が範囲の真ん中より左、ⅱ)軸が範囲の真ん中と一致、ⅲ)軸が範囲の真ん中より右

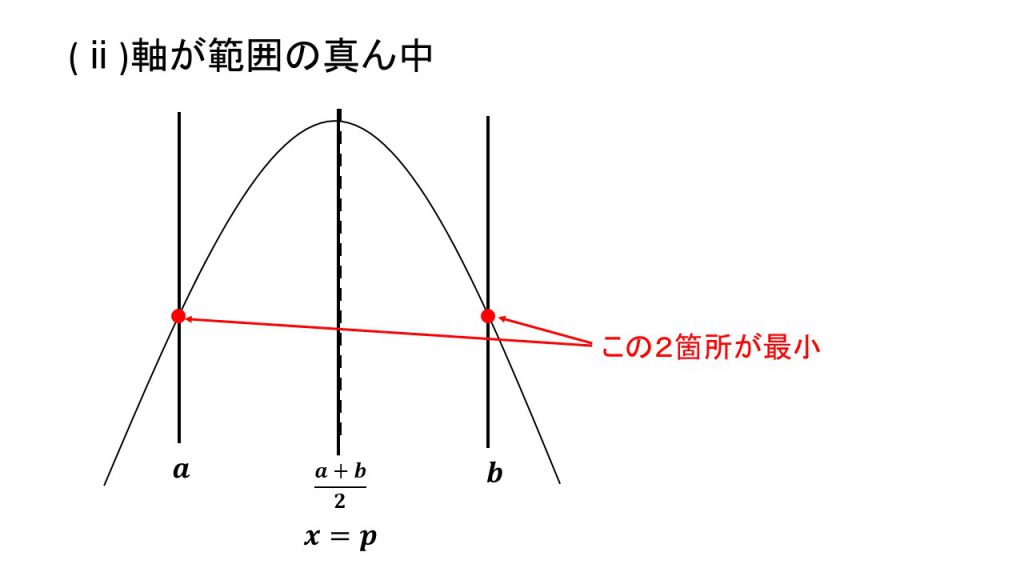

④上に凸で最大値
ⅰ)軸が範囲の左、ⅱ)軸が範囲の中、ⅲ)軸が範囲の右


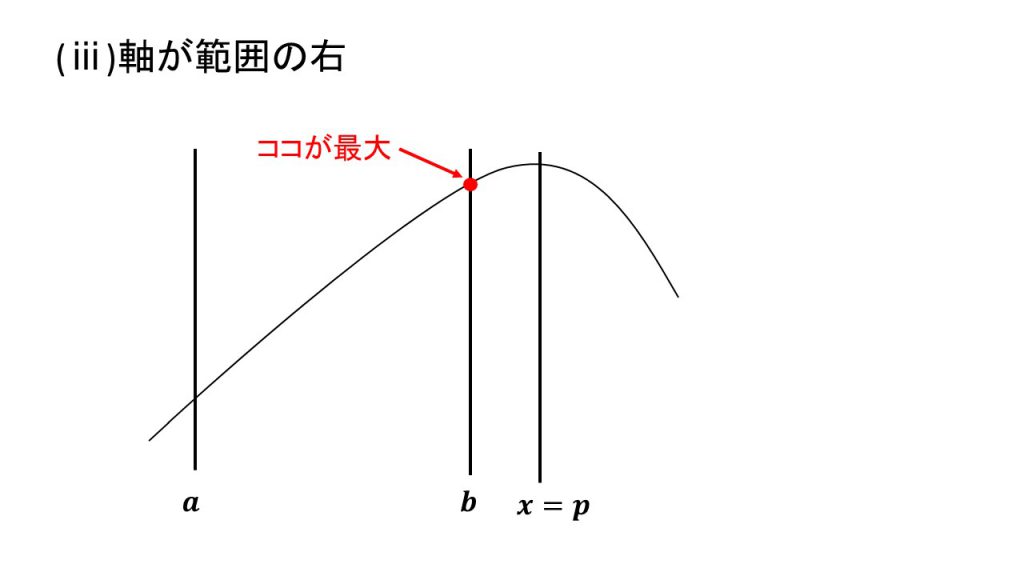
これらの場合分けの4パターンは覚えるというよりは、実際に3つの線と放物線をかいてみて理解するとよいでしょう。
(4)理解すべきコア(リンク先に動画があります)
二次関数の最大と最小を考えるときに引くべき3つの線を理解しましょう(場合分けについても解説しています)→二次関数の最大と最小を考えるときに引くべき3つの線
☆動画はこちら↓
