(1)例題
nを30以下の自然数とする。
p1:nは素数である
p2:n+2は素数である
q1:n+1は5の倍数ではない
q2:n+1は6の倍数である
命題「(p1かつp2)⇒(q1かつq2)」の反例を2つ答えよ。
(2015年センター試験本試数学ⅠA第2問〔1〕(2)より)
(2)例題の答案
(p1かつp2)を満たすものは
n=3, 5, 11, 17, 29
であり、その中で(q1かつq2)を満たさないものは
n=3, 29
よって反例は、n=3, 29
(3)解法のポイント
素数の定義は、
①約数が2つの自然数
です(ちなみに、素数の積で表せる自然数を合成数といいます)
また、素数の性質としては、
②1は素数ではない。
③2は唯一の偶数の素数(2以外の素数は奇数)
この3つを利用します。
特に③は重要です。
素数を答えるとき、2が答えになることが多く、
また2だけ特別扱いして場合分けをすることが多いです。
(4)必要な知識
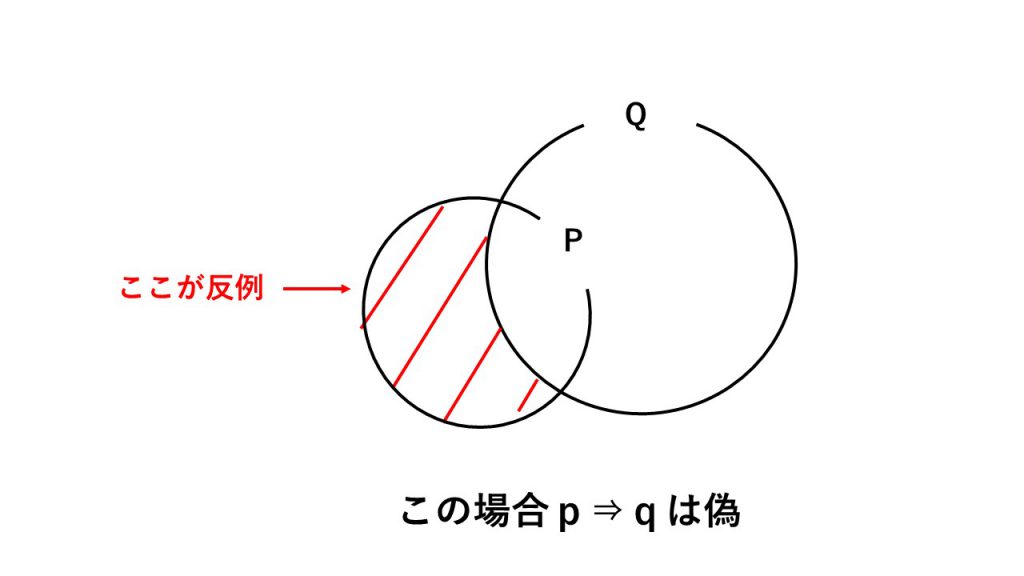
①反例の見つけ方
→pならばqの反例:pを満たし、かつ、qを満たさないもの